算法笔记 上机训练实战指南 第10章 提高篇(4)--图算法专题 学习笔记

10.3 图的遍历

PAT A1013 Battle Over Cities (25分)

It is vitally important to have all the cities connected by highways in a war. If a city is occupied by the enemy, all the highways from/toward that city are closed. We must know immediately if we need to repair any other highways to keep the rest of the cities connected. Given the map of cities which have all the remaining highways marked, you are supposed to tell the number of highways need to be repaired, quickly.

For example, if we have 3 cities and 2 highways connecting city​1​​-city​2​​ and city​1​​-city​3​​. Then if city​1​​ is occupied by the enemy, we must have 1 highway repaired, that is the highway city​2​​-city​3​​.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 3 numbers N (<), M and K, which are the total number of cities, the number of remaining highways, and the number of cities to be checked, respectively. Then M lines follow, each describes a highway by 2 integers, which are the numbers of the cities the highway connects. The cities are numbered from 1 to N. Finally there is a line containing K numbers, which represent the cities we concern.

Output Specification:

For each of the K cities, output in a line the number of highways need to be repaired if that city is lost.

Sample Input:

3 2 3
1 2
1 3
1 2 3

Sample Output:

1
0
0

#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
int n,m,k;
const int N = 1111;
vector<int> G[N];
bool vis[N];
int currentPoint;
void dfs(int v){
    if(v == currentPoint)
        return;
    vis[v] = true;
    for(int i=0;i<G[v].size();i++){
        if(vis[G[v][i]] == false)
            dfs(G[v][i]);
    }
}
int main(){
    scanf("%d%d%d",&n,&m,&k);
    for(int i=0;i<m;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        G[a].push_back(b);
        G[b].push_back(a);
    }
    for(int query = 0;query<k;query++){
        scanf("%d",&currentPoint);
        memset(vis,false,sizeof(vis));
        int block = 0;
        for(int i=1;i<=n;i++){
            if(i != currentPoint && vis[i]==false){
                dfs(i);
                block++;
            }
        }    
        printf("%d\n",block-1);
    }
    return 0;
}

PAT A1021 Deepest Root (25分)

A graph which is connected and acyclic can be considered a tree. The height of the tree depends on the selected root. Now you are supposed to find the root that results in a highest tree. Such a root is called the deepest root.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤) which is the number of nodes, and hence the nodes are numbered from 1 to N. Then N−1 lines follow, each describes an edge by given the two adjacent nodes' numbers.

Output Specification:

For each test case, print each of the deepest roots in a line. If such a root is not unique, print them in increasing order of their numbers. In case that the given graph is not a tree, print Error: K components where K is the number of connected components in the graph.

Sample Input 1:

5
1 2
1 3
1 4
2 5

Sample Output 1:

3
4
5

Sample Input 2:

5
1 3
1 4
2 5
3 4

Sample Output 2:

Error: 2 components

#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 10010;
vector<int> G[N];
bool isRoot[N];
int father[N];
int findFather(int x){
    int a = x;
    while(x != father[x]){
        x = father[x];
    }
    while(a != father[a]){
        int z = a;
        a = father[a];
        father[z] = x;
    }
    return x;
}
void Union(int a,int b){
    int faA = findFather(a);
    int faB = findFather(b);
    if(faA != faB){
        father[faA] = faB;
    }
}
void init(int n){
    for(int i=1;i <= n;i++){
        father[i] = i;
    }
}
int calBlock(int n){
    int Block = 0;
    for(int i = 1; i <= n;i++){
        isRoot[findFather(i)] = true;
    }
    for(int i = 1; i <= n ;i++){
        Block += isRoot[i];
    }
    return Block;
}
int maxH = 0;
vector<int> temp,Ans;
void DFS(int u,int Height,int pre){
    if(Height > maxH){
        temp.clear();
        temp.push_back(u);
        maxH = Height;
    }else if(Height == maxH){
        temp.push_back(u);
    }
    for(int i=0;i<G[u].size();i++){
        if(G[u][i] == pre)
            continue;
        DFS(G[u][i],Height+1,u);
    }
}
int main(){
    int a,b,n;
    scanf("%d",&n);
    init(n);
    for(int i=1;i<n;i++){
        scanf("%d%d",&a,&b);
        G[a].push_back(b);
        G[b].push_back(a);
        Union(a,b);
    }
    int Block = calBlock(n);
    if(Block != 1){
        printf("Error: %d components\n",Block);
    }else{
        DFS(1,1,-1);
        Ans = temp;
        DFS(Ans[0],1,-1);
        for(int i = 0;i < temp.size();i++){
            Ans.push_back(temp[i]);
        }
        sort(Ans.begin(),Ans.end());
        printf("%d\n",Ans[0]);
        for(int i = 1; i < Ans.size(); i++){
            if(Ans[i] != Ans[i-1]){
                printf("%d\n",Ans[i]);
            }
        }
    }
}

 PAT A1076 Forwards on Weibo (30分)

Weibo is known as the Chinese version of Twitter. One user on Weibo may have many followers, and may follow many other users as well. Hence a social network is formed with followers relations. When a user makes a post on Weibo, all his/her followers can view and forward his/her post, which can then be forwarded again by their followers. Now given a social network, you are supposed to calculate the maximum potential amount of forwards for any specific user, assuming that only L levels of indirect followers are counted.

Input Specification:

Each input file contains one test case. For each case, the first line contains 2 positive integers: N (≤), the number of users; and L (≤), the number of levels of indirect followers that are counted. Hence it is assumed that all the users are numbered from 1 to N. Then N lines follow, each in the format:

M[i] user_list[i]

 

where M[i] (≤) is the total number of people that user[i] follows; and user_list[i] is a list of the M[i] users that followed by user[i]. It is guaranteed that no one can follow oneself. All the numbers are separated by a space.

Then finally a positive K is given, followed by K UserID's for query.

Output Specification:

For each UserID, you are supposed to print in one line the maximum potential amount of forwards this user can trigger, assuming that everyone who can view the initial post will forward it once, and that only L levels of indirect followers are counted.

Sample Input:

7 3
3 2 3 4
0
2 5 6
2 3 1
2 3 4
1 4
1 5
2 2 6

Sample Output:

4
5

 

#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int MAXV = 1010;
struct Node{
    int id;
    int layer;
};
vector<Node> Adj[MAXV];
bool inq[MAXV] = {false};
int BFS(int s,int L){
    int numForward = 0;
    queue<Node> q;
    Node start;
    start.id = s;
    start.layer = 0;
    q.push(start);
    inq[start.id] = true;
    while(!q.empty()){
        Node topNode = q.front();
        q.pop();
        int u = topNode.id;
        for(int i=0;i < Adj[u].size();i++){
            Node next = Adj[u][i];
            next.layer = topNode.layer + 1;
            if(inq[next.id] == false && next.layer <= L){
                q.push(next);
                inq[next.id] = true;
                numForward++;
            }
        }
    }
    return numForward;
}
int main(){
    Node user;
    int n,L,numFollow,idFollow;
    scanf("%d%d",&n,&L);
    for(int i = 1; i <= n;i++){
        user.id = i;
        scanf("%d",&numFollow);
        for(int j = 0;j<numFollow;j++){
            scanf("%d",&idFollow);
            Adj[idFollow].push_back(user);
        }
    }    
    int numQuery,s;
    scanf("%d",&numQuery);
    for(int i=0;i<numQuery;i++){
        memset(inq,false,sizeof(inq));
        scanf("%d",&s);
        int numForward = BFS(s,L);
        printf("%d\n",numForward);
    }
     
    return 0;
}

 

10.4 最短路径

PAT A1003 Emergency (25分)

As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.

Input Specification:

Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (≤) - the number of cities (and the cities are numbered from 0 to N−1), M - the number of roads, C​1​​ and C​2​​ - the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c​1​​, c​2​​ and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C​1​​ to C​2​​.

Output Specification:

For each test case, print in one line two numbers: the number of different shortest paths between C​1​​ and C​2​​, and the maximum amount of rescue teams you can possibly gather. All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.

Sample Input:

5 6 0 2
1 2 1 5 3
0 1 1
0 2 2
0 3 1
1 2 1
2 4 1
3 4 1

Sample Output:

2 4

 

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXV = 510;
const int INF = 1000000000;
int n,m,st,ed,G[MAXV][MAXV],weight[MAXV];
int d[MAXV],w[MAXV],num[MAXV];
bool vis[MAXV] = {false};

void Dijkstra(int s){
    fill(d,d+MAXV,INF);
    memset(num,0,sizeof(num));
    memset(w,0,sizeof(w));
    d[s] = 0;
    w[s] = weight[s];
    num[s] = 1;
    for(int i=0;i<n;i++){
        int u = -1,MIN = INF;
        for(int j=0;j<n;j++){
            if(vis[j] == false && d[j]<MIN){
                u = j;
                MIN = d[j];
            }
        }
        if(u == -1)
            return;
        vis[u] = true;
        for(int v = 0;v < n;v++){
            if(vis[v] == false && G[u][v]!=INF){
                if(d[u] + G[u][v] < d[v]){
                    d[v] = d[u] + G[u][v];
                    w[v] = w[u] + weight[v];
                    num[v] = num[u];
                }else if(d[u] + G[u][v] == d[v]){
                    if(w[u] + weight[v] > w[v]){
                        w[v] = w[u] + weight[v];
                    }
                    num[v] += num[u]; 
                }
            }
        }
    }
}
int main(){
    scanf("%d%d%d%d",&n,&m,&st,&ed);
    for(int i = 0; i < n;i++){
        scanf("%d",&weight[i]);
    }
    int u,v;
    fill(G[0],G[0]+MAXV*MAXV,INF);
    for(int i = 0;i < m;i++){
        scanf("%d%d",&u,&v);
        scanf("%d",&G[u][v]);
        G[v][u] = G[u][v];
    } 
    Dijkstra(st);
    printf("%d %d\n",num[ed],w[ed]);
    return 0;
} 

 

PAT A1018 Public Bike Management (30分)

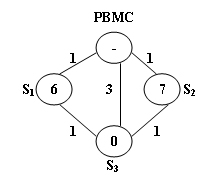
There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.

The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect condition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.

When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.

The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at S​3​​, we have 2 different shortest paths:

1. PBMC -> S​1​​ -> S​3​​. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from S​1​​ and then take 5 bikes to S​3​​, so that both stations will be in perfect conditions.

2. PBMC -> S​2​​ -> S​3​​. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.

Input Specification:

Each input file contains one test case. For each case, the first line contains 4 numbers: C​max​​ (≤), always an even number, is the maximum capacity of each station; N (≤), the total number of stations; S​p​​, the index of the problem station (the stations are numbered from 1 to N, and PBMC is represented by the vertex 0); and M, the number of roads. The second line contains N non-negative numbers C​i​​ (,) where each C​i​​ is the current number of bikes at S​i​​ respectively. Then M lines follow, each contains 3 numbers: S​i​​, S​j​​, and T​ij​​ which describe the time T​ij​​ taken to move betwen stations S​i​​ and S​j​​. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print your results in one line. First output the number of bikes that PBMC must send. Then after one space, output the path in the format: 0. Finally after another space, output the number of bikes that we must take back to PBMC after the condition of S​p​​ is adjusted to perfect.

Note that if such a path is not unique, output the one that requires minimum number of bikes that we must take back to PBMC. The judge's data guarantee that such a path is unique.

Sample Input:

10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1

Sample Output:

3 0->2->3 0

 

#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXV = 510;
const int INF = 1000000000;
int n,m,Cmax,Sp,numPath = 0,G[MAXV][MAXV],weight[MAXV];
int d[MAXV],minNeed = INF,minRemain = INF;
bool vis[MAXV] = {false};
vector<int> pre[MAXV];
vector<int> tempPath,path;

void Dijkstra(int s){
    fill(d,d+MAXV,INF);
    d[s] = 0;
    for(int i=0;i <= n;i++){
        int u = -1,MIN = INF;
        for(int j=0;j<=n;j++){
            if(vis[j] == false && d[j] < MIN){
                u = j;
                MIN = d[j];
            }
        }
        
        if(u == -1)
            return;
        vis[u] = true;
        for(int v = 0;v <= n; v++){
            if(vis[v] == false && G[u][v] != INF){
                if(d[u] + G[u][v] < d[v]){
                    d[v] = d[u] + G[u][v];
                    pre[v].clear();
                    pre[v].push_back(u);
                }else if(d[u] + G[u][v] == d[v]){
                    pre[v].push_back(u);
                }
            }
        }
    }
}
void DFS(int v){
    if(v == 0){
        tempPath.push_back(v);
        int need = 0,remain = 0;
        for(int i=tempPath.size() - 1;i >= 0;i--){
            int id = tempPath[i];
            if(weight[id] > 0){
                remain += weight[id];
            }else{
                if(remain > abs(weight[id])){
                    remain -= abs(weight[id]);
                }else{
                    need += abs(weight[id]) - remain;
                    remain = 0;
                }
            }
        }
        if(need < minNeed){
            minNeed = need;
            minRemain = remain;
            path = tempPath;
        }else if(need == minNeed && remain < minRemain){
            minRemain = remain;
            path = tempPath;
        }
        tempPath.pop_back();
        return;
    }
    tempPath.push_back(v);
    for(int i = 0 ;i<pre[v].size();i++){
        DFS(pre[v][i]);
    }
    tempPath.pop_back();
}

int main(){
    scanf("%d%d%d%d",&Cmax,&n,&Sp,&m);
    int u,v;
    fill(G[0],G[0] + MAXV * MAXV,INF);
    for(int i = 1; i <= n;i++){
        scanf("%d",&weight[i]);
        weight[i] -= Cmax/2;
    }
    for(int i=0;i<m;i++){
        scanf("%d%d",&u,&v);
        scanf("%d",&G[u][v]);
        G[v][u] = G[u][v];
    }
    Dijkstra(0);
    DFS(Sp);
    printf("%d ",minNeed);
    for(int i=path.size() - 1;i>= 0;i--){
        printf("%d",path[i]);
        if(i > 0)
            printf("->");
    }
    printf(" %d",minRemain);
    return 0;
}

PAT A1030 Travel Plan (30分)

A traveler's map gives the distances between cities along the highways, together with the cost of each highway. Now you are supposed to write a program to help a traveler to decide the shortest path between his/her starting city and the destination. If such a shortest path is not unique, you are supposed to output the one with the minimum cost, which is guaranteed to be unique.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 4 positive integers N, M, S, and D, where N (≤) is the number of cities (and hence the cities are numbered from 0 to N−1); M is the number of highways; S and D are the starting and the destination cities, respectively. Then M lines follow, each provides the information of a highway, in the format:

City1 City2 Distance Cost

where the numbers are all integers no more than 500, and are separated by a space.

Output Specification:

For each test case, print in one line the cities along the shortest path from the starting point to the destination, followed by the total distance and the total cost of the path. The numbers must be separated by a space and there must be no extra space at the end of output.

Sample Input:

4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20

Sample Output:

0 2 3 3 40

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXV = 510;
const int INF = 1000000000;
int n,m,st,ed,G[MAXV][MAXV];
int d[MAXV],cost[MAXV][MAXV],c[MAXV],pre[MAXV];
bool vis[MAXV] = {false};
void Dijkstra(int s){
    fill(d,d+MAXV,INF);
    fill(c,c+MAXV,INF);
    for(int i=0;i<n;i++)
        pre[i] = i;
    d[s] = 0;
    c[s] = 0;
    for(int i=0;i<n;i++){
        int u = -1,MIN = INF;
        for(int j=0;j<n;j++){
            if(vis[j]==false && d[j]<MIN){
                MIN = d[j];
                u = j;
            }
        }
        if(u == -1)
            return;
        vis[u] = true;
        for(int v=0;v<n;v++){
            if(d[u] + G[u][v] < d[v]){
                d[v] = d[u] + G[u][v];
                c[v] = c[u] + cost[u][v];
                pre[v] = u;
            }else if(d[u] + G[u][v] == d[v]){
                if(c[u] + cost[u][v] < c[v]){
                    c[v] = c[u] + cost[u][v];
                    pre[v] = u;
                }
            }
        } 
    }
}
void DFS(int v){
    if(v == st){
        printf("%d ",v);
        return;
    }
    DFS(pre[v]);
    printf("%d ",v);
}
int main(){
    scanf("%d%d%d%d",&n,&m,&st,&ed);
    int u,v;
    fill(G[0],G[0]+MAXV*MAXV,INF);
    for(int i=0;i<m;i++){
        scanf("%d%d",&u,&v);
        scanf("%d%d",&G[u][v],&cost[u][v]);
        G[v][u] = G[u][v];
        cost[v][u] = cost[u][v];
    }
    Dijkstra(st);
    DFS(ed);
    printf("%d %d\n",d[ed],c[ed]);
    return 0;
}