算法笔记第10章提高篇(4) --图算法专题学习笔记

10.1 图的定义和相关术语

图由顶点和边组成，每条边的两端都必须是图的两个顶点。而记号G(V,E)表示图G的顶点集为V、边集为E。

一般来说，图可分为有向图和无向图。有向图的所有边都有方向，即确定了顶点到顶点的一个指向；而无向图的所有边都是双向的，即无向边所连接的两个顶点可以互相到达。

10.2 图的存储

一般来说，图的存储方式有两种：邻接矩阵和邻接表。

10.2.1 邻接矩阵

令二维数组G[N][N]的两维分别表示图的顶点标号，即如果G[i][j]为1，则说明顶点i和顶点j之间有边；如果G[i][j]为0，则说明顶点i和顶点j之间不存在边，而这个二维数组G[][]则被称为邻接矩阵。

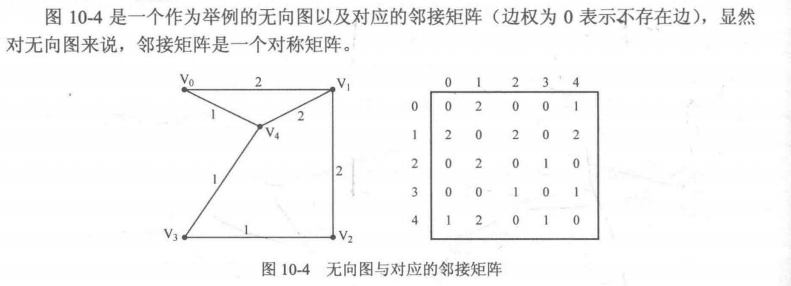
邻接矩阵只适用于顶点数目不太大（一般不超过1000）的题目。

10.2.2 邻接表

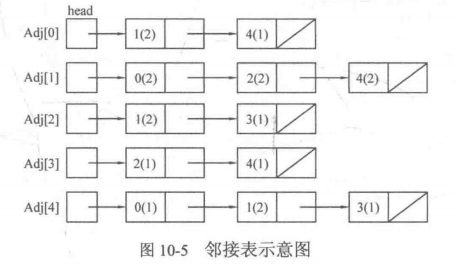
上图中，0号顶点有两条出边：一条的终点为1号顶点（边权为2）；另一条边的终点为4号顶点（边权为1）。

可以使用vector来实现邻接表。可以开一个vector数组Adj[N],其中N为顶点个数。如果想添加一条从1号顶点到达3号顶点的有向边，只需要在Adj[1]中添加终点编号3即可。

Adj[1].push_back(3);

如果需要同时存放边的终点编号和边权，那么可以建立结构体Node,用来存放每条边的终点编号和边权，代码如下所示：

struct Node{
    int v; //边的终点编号 
    int w; //边权 
};

这样vector邻接表中的元素类型就是Node型的，如下所示：

vector<Node> Adj[N];

此时如果想要添加从1号到达3号顶点的有向边，边权为4，就可以定义一个Node型的临时变量temp,令temp.v = 3,temp.w = 4，然后把temp加入到Adj[1]中即可。

Node[temp];

temp.v = 3;

temp.w = 4;

Adj[1].push_back(temp);

顶点数目较大的情况下，一般都需要使用邻接报而非邻接矩阵来存储图。

10.3 图的遍历

10.3.1 采用深度优先搜索(DFS)法遍历图

1.用DFS遍历图

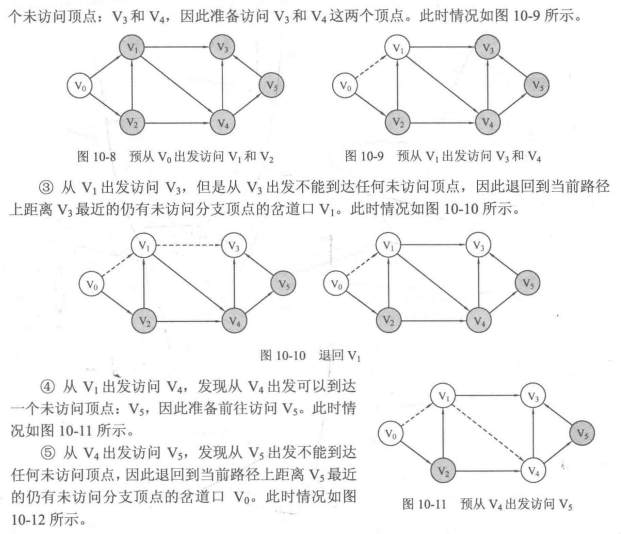
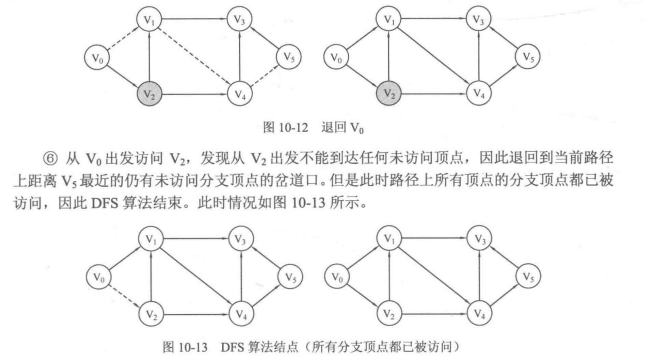
2.DFS的具体实现：

两个概念：

　　*连通分量：在无向图中，如果两个顶点之间可以相互到达，那么就称这两个顶点连通。如果图G(V,E)的任意两个顶点都连通，则称图G为连通图，否则，称图G为非连通图，且称其中的极大连通子图为连通分量。

　　*强连通分量：在有向图中，如果两个顶点可以各自通过一条有向路径到达另一个顶点，就称这两个顶点强连通。如果图G（V,E）的任意两个顶点都强连通，则称图G为强连通图；否则，称图G为非强连通图，且称其中的极大强连通子图为强连通分量。

①邻接矩阵版

const int MAXV = 1000; //最大顶点数 
const int INF = 1000000000;  //设INF为一个很大的数

int n,G[MAXV][MAXV]; //n为顶点数，MAXV为最大顶点数 
bool vis[MAXV] = {false}; //如果顶点i已被访问，则vis[i] == true。初值为false 
void DFS(int u,int depth){ //u为当前访问的顶点标号，depth为深度 
    vis[u] = true;
    //如果需要对u进行一些操作，可以在这里进行
    //下面对所有从u出发能到达的分支顶点进行枚举 
    for(int v = 0;v<n;v++){ //对每个顶点v 
        if(vis[v] == false && G[u][v] != INF){    //如果v未被访问，且u可到达v 
            DFS(v,depth+1);    //访问v，深度加1 
        }
    }
} 

void DFSTraver(){ //遍历图G 
    for(int u = 0; u < n; u++){    //对每个顶点u 
        if(vis[u] == false){    //如果u未被访问 
            DFS(u,1);    //访问u和u所在的连通块，1表示初始为第一层 
        }
    }
}

②邻接表版

const int MAXV = 1000; //最大顶点数 
const int INF = 1000000000;  //设INF为一个很大的数
vector<int> Adj[MAXV]; //图G的邻接表 
int n; //n为顶点数，MAXV为最大顶点数
bool vis[MAXV] = {false};

void DFS(int u,int depth){    //u为当前访问的顶点标号，depth为深度 
    vis[u] = true; //设置u已被访问
    /*如果需要对u进行一些操作，可以在此处进行*/
    for(int i = 0;i < Adj[u].size();i++){ //对从u出发可以到达的所有顶点v 
        int v = Adj[u][i];
        if(vis[v] == false){ //如果v未被访问 
            DFS(v,depth+1); //访问v，深度加1 
        }
    } 
} 

void DFSTrave(){    //遍历图G 
    for(int u = 0 ; u < n; u++){    //对每个顶点u 
        if(vis[u] == false){    //如果u未被访问 
            DFS(u,1);    //访问u和u所在的连通块，1表示初始为第一层 
        }
    }
}

10.3.2 采用广度优先搜索(BFS)法遍历图

1.用BFS遍历图

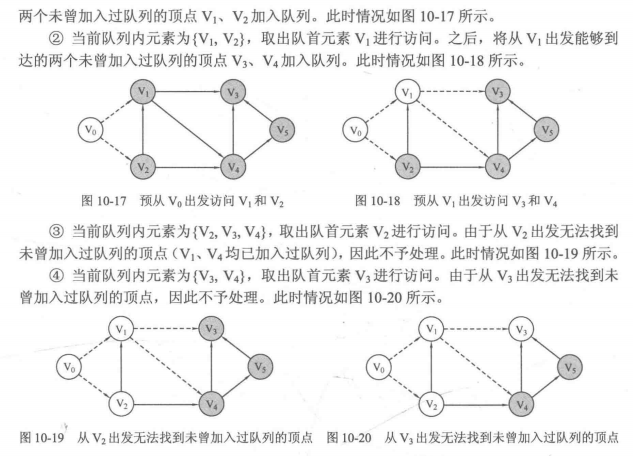
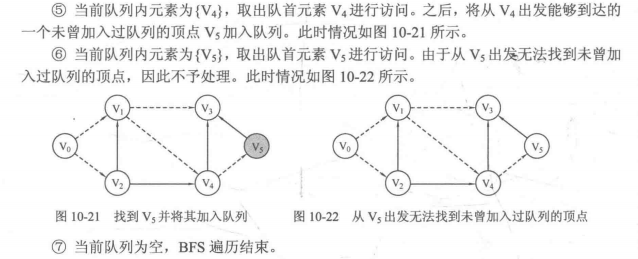
2. BFS的具体实现

1.邻接矩阵版

2. 邻接表版

PAT A1076 Forwards on Weibo (30分)

Weibo is known as the Chinese version of Twitter. One user on Weibo may have many followers, and may follow many other users as well. Hence a social network is formed with followers relations. When a user makes a post on Weibo, all his/her followers can view and forward his/her post, which can then be forwarded again by their followers. Now given a social network, you are supposed to calculate the maximum potential amount of forwards for any specific user, assuming that only

Input Specification:

Each input file contains one test case. For each case, the first line contains 2 positive integers:

M[i] user_list[i]

where M[i] ( $\leq) is the total number of people that user[i] follows; and user_list[i] is a list of the M[i] users that followed by user[i] . It is guaranteed that no one can follow oneself. All the numbers are separated by a space.$

Then finally a positive

Output Specification:

For each UserID, you are supposed to print in one line the maximum potential amount of forwards this user can trigger, assuming that everyone who can view the initial post will forward it once, and that only

Sample Input:

Sample Output:

4
5

#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int MAXV = 1010;
struct Node{
    int id;
    int layer;
};
vector<Node> Adj[MAXV];
bool inq[MAXV] = {false};
int BFS(int s,int L){
    int numForward = 0;
    queue<Node> q;
    Node start;
    start.id = s;
    start.layer = 0;
    q.push(start);
    inq[start.id] = true;
    while(!q.empty()){
        Node topNode = q.front();
        q.pop();
        int u = topNode.id;
        for(int i=0;i < Adj[u].size();i++){
            Node next = Adj[u][i];
            next.layer = topNode.layer + 1;
            if(inq[next.id] == false && next.layer <= L){
                q.push(next);
                inq[next.id] = true;
                numForward++;
            }
        }
    }
    return numForward;
}
int main(){
    Node user;
    int n,L,numFollow,idFollow;
    scanf("%d%d",&n,&L);
    for(int i = 1; i <= n;i++){
        user.id = i;
        scanf("%d",&numFollow);
        for(int j = 0;j<numFollow;j++){
            scanf("%d",&idFollow);
            Adj[idFollow].push_back(user);
        }
    }    
    int numQuery,s;
    scanf("%d",&numQuery);
    for(int i=0;i<numQuery;i++){
        memset(inq,false,sizeof(inq));
        scanf("%d",&s);
        int numForward = BFS(s,L);
        printf("%d\n",numForward);
    }
     
    return 0;
}

10.4 最短路径

最短路径是图论中一个很经典的问题：给定图G(V,E)，求一条从起点到终点的路径，使得这条路径上经过的所有边的边权之和最小。

也就是：对任意给出的图G(V,E)和起点S、终点T，如何求从S到T的最短路径。

10.4.1 Dijkstra算法

Dijkstra算法的基本思想是对图G(V,E)设置集合S，存放已被访问的顶点，然后每次从集合V-S中选择与起点s的最短距离最小的一个顶点(记为u)，访问并加入集合S。之后，令顶点u为中介点，优化起点s与所有从u到达的顶点v之间的最短距离。这样的操作执行n次，直到集合S已包含所有顶点。

①邻接矩阵版

const int MAXV = 1000; //最大顶点数
const int INF = 1000000000; //设INF为一个很大的数 
int n,G[MAXV][MAXV];    //nw为顶点数，MAXV为最大顶点数
int d[MAXV]; //起点到达各点的最短路径长度
bool vis[MAXV] = {false};

void Dijkstra(int s){    //s为起点
    fill(d,d+MAXV,INF);    //fill函数将整个d数组赋为INF 
    d[s] = 0;    //起点s到达自身的距离为0 
    for(int i = 0;i< n;i++){    //循环n次 
        int u = -1,MIN = INF;    //u使d[u]最小,MIN存放该最小的d[u] 
        for(int j = 0; j < n;j++){
            if(vis[j] == false && d[j]<MIN){
                u =j;
                MIN = d[j];
            }
        } 
    }
    //找不到小于INF的d[u]，说明剩下的顶点和起点s不连通
    if(u == -1)
        return;
    vis[u] = true;    //标记u为已访问
    for(int v = 0; v < n;v++){
        //如果v未访问&& u能到达v && 以u为中介点可以使d[v]更优
        if(vis[v]==false && G[u][v] != INF && d[u] + G[u][v] < d[v]){
            d[v] = d[u] + G[u][v]; //优化d[v] 
        } 
    } 
}

②邻接表版

const int MAXV = 1000; //最大顶点数
const int INF = 1000000000; //设INF为一个很大的数 
struct Node{
    int v,dis;    //v为边的目标顶点，dis为边权 
};
vector<Node> Adj[MAXV]; //图G，Adj[u]存放从顶点u出发可以到达的所有顶点 
int n;    //n为顶点数
int d[MAXV]; //起点到达各点的最短路径长度
bool vis[MAXV] = {false};    //标记数组，vis[i] ==true表示已访问。初值均为false 

void Dijkstra(int s){    //s为起点
    fill(d,d+MAXV,INF);    //fill函数将整个d数组赋为INF 
    d[s] = 0;    //起点s到达自身的距离为0 
    for(int i = 0;i< n;i++){    //循环n次 
        int u = -1,MIN = INF;    //u使d[u]最小,MIN存放该最小的d[u] 
        for(int j = 0; j < n;j++){
            if(vis[j] == false && d[j]<MIN){
                u =j;
                MIN = d[j];
            }
        } 
    }
    //找不到小于INF的d[u]，说明剩下的顶点和起点s不连通
    if(u == -1)
        return;
    vis[u] = true;    //标记u为已访问
    for(int j = 0; j < Adj[u].size() ;j++){
        int v = Adj[u][j].v; //通过邻接表直接获得u能到达的顶点v 
        if(vis[v]==false && d[u]+Adj[u][j].dis < d[v]){
            d[v] = d[u] + Adj[u][j].dis; //优化d[v] 
        } 
    } 
}

PAT A1003 Emergency (25分)

As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.

Input Specification:

Each input file contains one test case. For each test case, the first line contains 4 positive integers:

Output Specification:

For each test case, print in one line two numbers: the number of different shortest paths between

Sample Input:

Sample Output:

2 4

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXV = 510;
const int INF = 1000000000;
int n,m,st,ed,G[MAXV][MAXV],weight[MAXV];
int d[MAXV],w[MAXV],num[MAXV];
bool vis[MAXV] = {false};

void Dijkstra(int s){
    fill(d,d+MAXV,INF);
    memset(num,0,sizeof(num));
    memset(w,0,sizeof(w));
    d[s] = 0;
    w[s] = weight[s];
    num[s] = 1;
    for(int i=0;i<n;i++){
        int u = -1,MIN = INF;
        for(int j=0;j<n;j++){
            if(vis[j] == false && d[j]<MIN){
                u = j;
                MIN = d[j];
            }
        }
        if(u == -1)
            return;
        vis[u] = true;
        for(int v = 0;v < n;v++){
            if(vis[v] == false && G[u][v]!=INF){
                if(d[u] + G[u][v] < d[v]){
                    d[v] = d[u] + G[u][v];
                    w[v] = w[u] + weight[v];
                    num[v] = num[u];
                }else if(d[u] + G[u][v] == d[v]){
                    if(w[u] + weight[v] > w[v]){
                        w[v] = w[u] + weight[v];
                    }
                    num[v] += num[u]; 
                }
            }
        }
    }
}
int main(){
    scanf("%d%d%d%d",&n,&m,&st,&ed);
    for(int i = 0; i < n;i++){
        scanf("%d",&weight[i]);
    }
    int u,v;
    fill(G[0],G[0]+MAXV*MAXV,INF);
    for(int i = 0;i < m;i++){
        scanf("%d%d",&u,&v);
        scanf("%d",&G[u][v]);
        G[v][u] = G[u][v];
    } 
    Dijkstra(st);
    printf("%d %d\n",num[ed],w[ed]);
    return 0;
}

PAT A1030 Travel Plan (30分)

A traveler's map gives the distances between cities along the highways, together with the cost of each highway. Now you are supposed to write a program to help a traveler to decide the shortest path between his/her starting city and the destination. If such a shortest path is not unique, you are supposed to output the one with the minimum cost, which is guaranteed to be unique.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 4 positive integers

City1 City2 Distance Cost

where the numbers are all integers no more than 500, and are separated by a space.

Output Specification:

For each test case, print in one line the cities along the shortest path from the starting point to the destination, followed by the total distance and the total cost of the path. The numbers must be separated by a space and there must be no extra space at the end of output.

Sample Input:

Sample Output:

0 2 3 3 40

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXV = 510;
const int INF = 1000000000;
int n,m,st,ed,G[MAXV][MAXV];
int d[MAXV],cost[MAXV][MAXV],c[MAXV],pre[MAXV];
bool vis[MAXV] = {false};
void Dijkstra(int s){
    fill(d,d+MAXV,INF);
    fill(c,c+MAXV,INF);
    for(int i=0;i<n;i++)
        pre[i] = i;
    d[s] = 0;
    c[s] = 0;
    for(int i=0;i<n;i++){
        int u = -1,MIN = INF;
        for(int j=0;j<n;j++){
            if(vis[j]==false && d[j]<MIN){
                MIN = d[j];
                u = j;
            }
        }
        if(u == -1)
            return;
        vis[u] = true;
        for(int v=0;v<n;v++){
            if(d[u] + G[u][v] < d[v]){
                d[v] = d[u] + G[u][v];
                c[v] = c[u] + cost[u][v];
                pre[v] = u;
            }else if(d[u] + G[u][v] == d[v]){
                if(c[u] + cost[u][v] < c[v]){
                    c[v] = c[u] + cost[u][v];
                    pre[v] = u;
                }
            }
        } 
    }
}
void DFS(int v){
    if(v == st){
        printf("%d ",v);
        return;
    }
    DFS(pre[v]);
    printf("%d ",v);
}
int main(){
    scanf("%d%d%d%d",&n,&m,&st,&ed);
    int u,v;
    fill(G[0],G[0]+MAXV*MAXV,INF);
    for(int i=0;i<m;i++){
        scanf("%d%d",&u,&v);
        scanf("%d%d",&G[u][v],&cost[u][v]);
        G[v][u] = G[u][v];
        cost[v][u] = cost[u][v];
    }
    Dijkstra(st);
    DFS(ed);
    printf("%d %d\n",d[ed],c[ed]);
    return 0;
}

10.4.2 Bellman-Ford算法和SPFA算法

如果出现了负边权，Dijkstra算法就会失效。

10.4.3 Floyd算法

#include<cstdio>
#include<algorithm>
using namespace std;
const int INF = 1000000000;
const int MAXV = 200;    //MAXV为最大顶点数 
int n,m; //n为顶点数，m为边数 
int dis[MAXV][MAXV];

void Floyd(){
    for(int k = 0;k < n;k++){
        for(int i = 0;i < n;i++){
            for(int j = 0;j < n;j++){
                if(dis[i][k] != INF && dis[k][j] != INF && dis[i][k] + dis[k][j] < dis[i][j]){
                    dis[i][j] = dis[i][k] + dis[k][j];
                }
            }
        }
    }
} 
int main(){
    int u,v,w;
    fill(dis[0],dis[0]+MAXV*MAXV,INF);
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++){
        dis[i][i] = 0;
    }
    for(int i=0;i < m;i++){
        scanf("%d%d%d",&u,&v,&w);
        dis[u][v] = w;
    }
    Floyd();
    for(int i=0;i<n;i++){
        for(int j = 0;j < n;j++){
            printf("%d ",dis[i][j]);
        }
        printf("\n");
    }
    return 0;
}

10.5 最小生成树

10.5.1 最小生成树及其性质

最小生成树是在一个给定的无向图G(V,E)中求一棵树T，使得这棵树拥有图G中的所有顶点，且所有边都是来自图G中的边，并且满足整棵树的边权之和最小。

最小生成树的性质：

①最小生成树是树，因此其边数等于顶点数减1，且树内一定不会有环。

②对给定的图G(V,E),其最小生成树可以不唯一，但其边权之和一定是唯一的。

③由于最小生成树是在无向图上生成的，因此其根结点可以是这棵树上的任意一个结点。

10.5.2 prim算法

prim算法的基本思想是对图G(V,E)设置集合S(即巨型防护罩)来存放已被访问的顶点，然后执行n次下面的两个步骤(n为顶点个数)：

①每次从集合V-S中选择与集合S最近的一个顶点，访问u并将其加入集合S，同时把这条离集合S最近的边加入最小生成树中。

②令顶点u作为集合S与集合V-S连接的接口，优化从u能到达的未访问顶点v与集合S的最短距离。

邻接矩阵版

const int MAXV = 1000;
const int INF = 1000000000;
int n,G[MAXV][MAXV]; //n为顶点数，MAXV为最大顶点数 
int d[MAXV];    //顶点与集合S的最短距离 
bool vis[MAXV] = {false};    //标记数组，vis[i] == true表示已访问。初值均为false 

int prim(){ //默认0号为初始点，函数返回最小生成树的边权之和 
    fill(d,d+MAXV,INF);  //fill函数将整个d数组赋为INF 
    d[0] = 0; //只有0号顶点到集合S的距离为0，其余全为INF 
    int ans = 0; //存放最小生成树的边权之和  
    for(int i = 0; i < n; i++){    //循环n次 
        int u = -1,MIN = INF; //u使d[u]最小，MIN存放该最小的d[u] 
        for(int j = 0; j < n;j++){    //找到未访问的顶点中d[]最小的 
            if(vis[j] == false && d[j] < MIN){
                u = j;
                MIN = d[j];
            }
        }
        //找不到小于INF的d[u],则剩下的顶点和集合S不连通 
        if(u == -1)
            return -1;
        vis[u] = true; //标记u为已访问 
        ans += d[u]; //将与集合S距离最小的边加入最小生成树 
        for(int v = 0; v< n;v++){
            //v访问 && u能到达v && 以u为中介点可以使v离集合S更近 
            if(vis[v] == false && G[u][v] != INF && G[u][v] < d[v]){
                d[v] = G[u][v]; //将G[u][v]赋值给d[v] 
            }
        }
    } 
    return ans; //返回最小生成树的边权之和 
}

邻接表版

const int MAXV = 1000;
const int INF = 1000000000;
struct Node{
    int v,dis; //v为边的目标顶点，dis为边权 
};
vector<Node> Adj[MAXV]; //图G，Adj[u]存放从顶点u出发可以到达的所有顶点 
int n; //n为顶点数 
int d[MAXV];    //顶点与集合S的最短距离 
bool vis[MAXV] = {false};    //标记数组，vis[i] == true表示已访问。初值均为false 

int prim(){ //默认0号为初始点，函数返回最小生成树的边权之和 
    fill(d,d+MAXV,INF);  //fill函数将整个d数组赋为INF 
    d[0] = 0; //只有0号顶点到集合S的距离为0，其余全为INF 
    int ans = 0; //存放最小生成树的边权之和  
    for(int i = 0; i < n; i++){    //循环n次 
        int u = -1,MIN = INF; //u使d[u]最小，MIN存放该最小的d[u] 
        for(int j = 0; j < n;j++){    //找到未访问的顶点中d[]最小的 
            if(vis[j] == false && d[j] < MIN){
                u = j;
                MIN = d[j];
            }
        }
        //找不到小于INF的d[u],则剩下的顶点和集合S不连通 
        if(u == -1)
            return -1;
        vis[u] = true; //标记u为已访问 
        ans += d[u]; //将与集合S距离最小的边加入最小生成树 
        for(int v = 0; v< n;v++){
            int v = Adj[u][j].v; //通过邻接表直接获得u能到达的顶点v 
            if(vis[v] == false && Adj[u][v].dis < d[v]){
                d[v] = Adj[u][v].dis; 
            }
        }
    } 
    return ans; //返回最小生成树的边权之和 
}

10.5.3 kruskal算法

kruskal算法的思想简单说来就是：每次选择图中最小边权的边，如果边两端的顶点在不同的连痛块中，就把这条边加入最小生成树中。

10.6 拓扑排序

10.6.1 有向无环图

如果一个有向图的任意顶点都无法通过一些有向边回到自身，那么称这个有向图为有向无环图。

10.6.2 拓扑排序

拓扑排序是将有向无环图G的所有顶点排成一个线性序列，使得对图G中的任意两个顶点u、v，如果存在边u->v,那么在序列中u一定在v前面，这个序列又被称为拓扑序列。

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXV = 110;
const int MAXE = 10010;
struct edge{
    int u,v;  //边的两个端点编号
    int cost; //边权 
}E[MAXE]; //最多有MAXE条边
bool cmp(edge a,edge b){
    return a.cost < b.cost; 
} 
int father[MAXV];
int findFather(int x){
    int a = x;
    while(x != father[x]){
        x = father[x];
    }
    while(a != father[a]){
        int z = a;
        a = father[a];
        father[z] = x;
    }
    return x;
}
int kruskal(int n,int m){
    int ans = 0,Num_Edge = 0;
    for(int i = 0;i < n; i++){
        father[i] = i;
    }
    sort(E,E+m,cmp);
    for(int i = 0; i < m;i++){
        int faU = findFather(E[i].u);
        int faV = findFather(E[i].v);
        if(faU != faV){
            father[faU] = faV;
            ans += E[i].cost;
            Num_Edge++;
            if(Num_Edge == n-1)
                break;
        }
    }
    if(Num_Edge != n-1)
        return -1;
    else
        return ans;
}
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i = 0; i < m; i++){
        scanf("%d%d%%d",&E[i].u,&E[i].v,&E[i].cost); 
    }
    int ans = kruskal(n,m);
    printf("%d\n",ans);
    return 0;
}

10.7 关键路径

10.7.1 AOV网和AOE网

posted @ 2020-02-09 14:50 程序员小应阅读(262) 评论(0) 编辑收藏举报

刷新页面返回顶部

程序员小应

算法笔记 第10章 提高篇(4) --图算法专题 学习笔记

Input Specification:

Output Specification:

Sample Input:

Sample Output:

Input Specification:

Output Specification:

Sample Input:

Sample Output:

Input Specification:

Output Specification:

Sample Input:

Sample Output:

公告

算法笔记第10章提高篇(4) --图算法专题学习笔记