算法笔记第9章提高篇(3) --数据结构专题(2) 学习笔记

9.1 树与二叉树

9.1.1 树的定义与性质

数据结构中把树枝分叉处、树叶、树根抽象为结点，其中树根抽象为根结点，且对一棵树来说最多存在一个根节点；把树叶概括为叶子结点，且叶子结点不再延伸出新的结点；把茎干和树枝统一抽象为边，且一条边只用来连接两个结点。

下面给出几个比较实用的概念和性质：

① 空树：没有结点的树

② 树的层次：从根结点开始算起，即根结点为第一层，根结点子树的根结点为第二次，以此类推

③ 结点的度：结点的子树棵树，树的度：树中结点最大的度

④ 满足连通、边数等于顶点数减1的结构一定是一棵树

⑤ 叶子结点：度为0的结点

⑥ 结点的深度：从根结点开始自顶向下逐层累加至该结点时的深度值；结点的高度是指从最底层叶子结点开始自底向上逐层累加至该结点时的高度值。对树而言，深度和高度是相等的。

⑦ 多棵树组合在一起称为森林，即森林是若干棵树的集合。

9.1.2 二叉树的递归定义

① 要么二叉树没有根结点，是一棵空树。

② 要么二叉树由根结点、左子树、右子树组成，且左子树和右子树都是二叉树。

二叉树与度为2的树的区别：二叉树虽然也满足每个结点的子结点个数不超过2，但它的左右子树是严格区分的，不能随意交换左子树和右子树的位置。

两种特殊的二叉树：

①满二叉树：每一层的结点个数都达到了当层能达到的最大结点数。

②完全二叉树：除了最下面一层之外，其余层的结点个数都达到了当层能达到的最大结点数，且最下面一层只从左至右连续存在若干结点，而这些连续结点右边的结点全部不存在。

9.1.3 二叉树的存储结构与基本操作

1.二叉树的存储结构

struct node{
    typename data; // 数据域
    node* lchild;  //指向左子树根结点的指针 
    node* rchild;  //指向右子树根结点的指针 
};

2.新建结点函数：

//生成一个新结点，v为结点权值 
node* newNode(int v){
    node* Node = new node;     //申请一个node型变量的地址空间 
    Node->data = v;        //结点权值为v 
    Node->lchild = Node->rchild = NULL;     //初始状态下没有左右孩子 
    return Node;     //返回新建结点的地址 
}

3.二叉树结点的查找

void search(node* root,int x,int newdata){
    if(root == NULL){
        return; //空树，死胡同(递归边界) 
    }
    if(root->data == x){
        root->data = newdata;
    }
    search(root->lchild,x,newdata);
    search(root->rchild,x,newdata);
}

4.二叉树结点的插入

//insert函数将在二叉树中插入一个数据域为x的新结点
//注意根结点指针root要使用引用，否则插入不会成功
void insert(node* &root,int x){
    if(root == NULL){
        root = newNode(x);
        return;
    }
    if(由二叉树的性质,x应该插在左子树){
        insert(root->lchild,x); //往左子树搜索(递归式) 
    }else{
        insert(root->rchild,x); //往右子树搜索(递归式) 
    }
}

5.二叉树的创建

//二叉树的建立
node* Create(int data[],int n){
    node* root = NULL; //新建空根结点root 
    for(int i = 0; i < n ;i++){
        insert(root,data[i]); //将data[0]~data[n-1]插入二叉树中 
    }
    return root; //返回根结点 
}

9.2 二叉树的遍历

二叉树的遍历是指通过一定顺序访问二叉树的所有结点。遍历方法一般有四种：先序遍历、中序遍历、后序遍历以及层次遍历，其中，前三种一般使用深度优先搜索实现，而层次遍历一般用广度优先搜索实现。

9.2.1 先序遍历

1.先序遍历的实现

先序遍历的遍历顺序是根结点->左子树->右子树

void preorder(node* root){
    if(root == NULL){
        return; //到达空树，递归边界 
    }
    //访问根结点root，例如将其数据域输出
    printf("%d\n",root->data);
    //访问左子树
    preorder(root->lchild);
    //访问右子树 
    preorder(root->rchild);
}

2.先序遍历序列的性质

序列的第一个一定是根结点。

9.2.2 中序遍历

1.中序遍历的实现

中序遍历的遍历顺序是:左子树-->根结点-->右子树

void inorder(node* root){
    if(root == NULL){
        return; //到达空树，递归边界 
    }
    //访问左子树
    inorder(root->lchild);
    //访问根结点root,例如将其输出
    printf("%d\n",root->data);
    //访问右子树
    inorder(root->rchild); 
}

2.中序遍历序列的性质

由于中序遍历总是把根结点放在左子树和右子树中间，因此只要知道根结点，就可以通过根结点在中序遍历序列中的位置区分出左子树和右子树。

9.2.3 后序遍历

1.后序遍历的实现

后序遍历的遍历顺序是左子树-->右子树-->根结点

void postorder(node* root){
    if(root == NULL){
        return; //到达空树，递归边界 
    }
    //访问左子树
    postorder(root->lchild);
    //访问右子树 
    postorder(root->rchild); 
    //访问根结点root，例如将其数据域输出
    printf("%d\n",root->data); 
}

2.后序遍历序列的性质

后序遍历的最后一个一定是根结点。

无论是先序遍历序列还是后序遍历序列，都必须知道中序遍历序列才能唯一地确定一棵树。

9.2.4 层序遍历

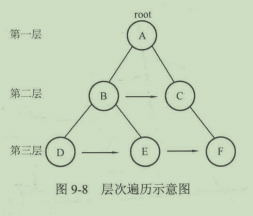
层序遍历的过程和BFS很像。

层序遍历的基本思路如下：

① 将根结点root加入队列q

② 取出队首结点，访问它。

③ 如果该结点有左孩子将左孩子入队。

④ 如果该结点有右孩子将右孩子入队。

⑤ 返回②，直到队列为空。

//层序遍历
void LayerOrder(node* root){
    queue<node*> q;
    q.push(root);
    while(!q.empty()){
        node* now = q.front();
        q.pop();
        printf("%d",now->data);
        if(now->lchild != NULL)
            q.push(now->lchild);
        if(now->rchild != NULL)
            q.push(now->rchild);
    }
}

PAT A1020 Tree Traversals (25分)

Suppose that all the keys in a binary tree are distinct positive integers. Given the postorder and inorder traversal sequences, you are supposed to output the level order traversal sequence of the corresponding binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer

Output Specification:

For each test case, print in one line the level order traversal sequence of the corresponding binary tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

Sample Output:

4 1 6 3 5 7 2

#include<cstdio>
#include<queue>
using namespace std;
int n;
const int maxn = 50;
int post[maxn],in[maxn];
struct node{
    int data;
    node* lchild;
    node* rchild;
};
node* create(int postL,int postR,int inL,int inR){
    if(postL > postR){
        return NULL;
    }
    node* root = new node;
    root->data = post[postR];
    int numleft,k;
    for(k=inL;k<=inR;k++){
        if(in[k] == post[postR]){
            break;
        }
    }
    numleft = k - inL;
    root->lchild = create(postL,postL+numleft-1,inL,k - 1);
    root->rchild = create(postL+numleft,postR-1,k + 1,inR);
    return root;
}
void BFS(node* root){
    queue<node*> q;
    q.push(root);
    int num = 0;
    while(!q.empty()){
        node* now = q.front();
        q.pop();
        printf("%d",now->data);
        num++;
        if(num < n){
            printf(" ");
        }
        if(now->lchild != NULL)
            q.push(now->lchild);
        if(now->rchild != NULL)
            q.push(now->rchild);
    }
}
int main(){
    scanf("%d",&n);
    for(int i = 0; i < n; i++){
        scanf("%d",&post[i]);
    }
    for(int i = 0; i < n; i++){
        scanf("%d",&in[i]);
    }
    node* root = create(0,n-1,0,n-1);
    BFS(root);
    return 0;
}

9.2.5 二叉树的静态实现

struct node{
    typename data;    //数据域 
    int lchild;        //指向左子树的指针域 
    int rchild;        //指向右子树的指针域 
}Node[maxn];     //结点数组，maxn为结点上限个数

结点的动态生成

int index = 0;
int newNode(int v){ //分配一个Node数组中的结点给新的结点，index为其下标 
    Node[index].data = v;     //数据域为v 
    Node[index].lchild = -1;    //以-1或maxn表示空，因为数组范围是0-maxn-1 
    Node[index].rchild = -1;
    return index++;
}

静态二叉树的查找、插入、建立

//查找，root为根结点在数组中的下标
void search(int root,int x,int newdata){
    if(root == -1){ //用-1来代替NULL 
        return; //空树，死胡同(递归边界) 
    }
    if(Node[root].data == x){ //找到数据域为x的结点，把它修改成newdata 
        Node[root].data = newdata;
    }
    search(Node[root].lchild, x, newdata); //往左子树搜索x(递归式)
    search(Node[root].rchild, x, newdata); //往右子树搜索x(递归式) 
} 

//插入，root为根结点在数组中的下标
void insert(int &root,int x){
    if(root == -1){
        root = newNode(x);
        return;
    }
    if(由二叉树的性质x应该插在左子树){
        insert(Node[root].lchild,x);
    }else{
        insert(Node[root].lchild,x);
    }
} 

//二叉树的建立，函数返回根结点root的下标
int Create(int data[],int n){
    int root = -1;
    for(int i=0;i<n;i++){
        insert(root,data[i]);
    }
    return root;
}

9.3 树的遍历

9.3.1 树的静态写法

本节讨论的”树“是指一般意义上的树，即子结点个数不限且子结点没有先后次序的树。

struct node{
    typename data;        //数据域 
    int child[maxn];    //指针域，存放所有子结点的下标 
}Node[maxn];    //结点数组，maxn为结点上限个数

在上面的定义中，由于无法预知子结点个数，因此child数组的长度只能开到最大，而这对一些结点个数较多的题目来说显然是不可接受的，因此需要使用STL中的vector,即长度根据实际需要而自动变化的”数组“。

struct node{
    typename data; //数据域
    vector child;    //指针域，存放所有子结点的下标 
}Node[maxn];    //结点数组，maxn为结点上限个数

9.3.2 树的先根遍历

先访问根结点，再去访问所有子树。

void PreOrder(int root){
    printf("%d ",Node[root],data);    //访问当前结点 
    for(int i = 0; i < Node[root].child.size(); i++){
        PreOrder(Node[root].child[i]);    //递归访问结点root的所有子结点 
    }
}

9.3.3 树的层序遍历

void LayerOrder(int root){
    queue<int> Q;
    Q.push(root);
    while(!Q.empty()){
        int front = Q.front();    //取出队首元素 
        printf("%d ",Node[front].data);    //访问当前结点的数据域 
        Q.pop();
        for(int i = 0 ; i<Node[front].child.size(); i++){
            Q.push(Node[front].child[i]);    //将当前结点的所有子结点入队 
        }
    }
}

9.3.4 从树的遍历看DFS与BFS

1.深度优先搜索(DFS)与先根遍历

对所有合法的DFS求解过程，都可以把它画成树的形式。于是可以得到启发，碰到一些可以用DFS做的题目，不妨把一些状态作为树的结点，然后问题就会转换为直观的对树进行先根遍历的问题。

2.广度优先搜索(BFS)与层序遍历

对所有合法的BFS求解过程，都可以像DFS中那样画出一棵树，并且将广度优先搜索问题转换为树的层序遍历的问题。

9.4 二叉查找树(BST)

9.4.1 二叉查找树的定义

二叉查找树是一种特殊的二叉树，又称为排序二叉树、二叉搜索树、二叉排序树。二叉查找树的递归定义如下：

（1）要么二叉查找树是一棵空树。

（2）要么二叉查找树由根结点、左子树、右子树组成，其中左子树和右子树都是二叉查找树，且左子树上所有结点的数据域均小于或等于根结点的数据域，右子树上所有结点的数据域均大于根结点的数据域。

9.4.2 二叉查找树的基本操作

1.查找操作

二叉查找树的性质决定了可以只选择其中一棵子树进行遍历。

//search函数查找二叉查找树中数据域为x的结点 
void search(node* root,int x){
    if(root == NULL){    //空树，查找失败 
        printf("search failed\n");
        return;
    }
    if(x == root->data){    //查找成功，访问之 
        printf("%d\n",root->data);
    }else if(x < root->data){    //如果x比根结点的数据域小，说明x在左子树 
        search(root->lchild,x);
    }else{    //如果x比根结点的数据域大，说明x在右子树 
        search(root->rchild,x);
    }
}

2. 插入操作

//insert函数将在二叉树中插入一个数据域为x的新结点(注意参数root要加引用&)
void insert(node* &root,int x){
    if(root == NULL){ //空树，说明查找失败，也即插入位置 
        root = newNode(x); //新建结点，权值为x
        return; 
    }
    if(x == root->data){ //查找成功，说明结点已存在，直接返回 
        return;
    }else if(x < root->data){    //如果x比根结点的数据域小，说明x需要插在左子树 
        insert(root->lchild,x);
    }else{ //如果x比根结点的数据域大，说明x需要插在右子树 
        insert(root->rchild,x);
    }
}

3.二叉树的建立

//二叉查找树的建立
node* Create(int data[],int n){
    node* root = NULL; //新建根结点root
    for(int i=0;i<n;i++) {
        insert(root,data[i]); //将data[0] ~ data[n-1]插入二叉查找树中 
    }
    return root; //返回根结点 
}

4.二叉查找树的删除

//寻找以root为根结点的树中的最大权值结点
node* findMax(node* root){
    while(root->rchild != NULL){
        root = root->rchild;
    }
    return root;
} 
//寻找以root为根结点的树中的最小权值结点
node* findMin(node* root){
    while(root->lchild != NULL){
        root = root->lchild;
    }
    return root;
} 
//删除以root为根结点的树中权值为x的结点
void deleteNode(node* &root,int x){
    if(root == NULL)
        return;
    if(root->data == x){
        if(root->lchild==NULL && root->rchild == NULL){
            root = NULL;
        }else if(root->lchild != NULL){
            node* pre = findMax(root->lchild);
            root->data = pre->data;
            deleteNode(root->lchild,pre->data);
        }else{
            node* nextt = findMin(root->rchild);
            root->data = next->data;
            deleteNode(root->rchild,next->data);
        }
    }else if(root->data > x){
        deleteNode(root->lchild,x);
    }else{
        deleteNode(root->rchild,x);
    }
}

9.4.3 二叉查找树的性质

对二叉查找树进行中序遍历，遍历的结果是有序的。

PAT A1043 Is It a Binary Search Tree (25分)

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
Both the left and right subtrees must also be binary search trees.

If we swap the left and right subtrees of every node, then the resulting tree is called the Mirror Image of a BST.

Now given a sequence of integer keys, you are supposed to tell if it is the preorder traversal sequence of a BST or the mirror image of a BST.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer

Output Specification:

For each test case, first print in a line YES if the sequence is the preorder traversal sequence of a BST or the mirror image of a BST, or NO if not. Then if the answer is YES, print in the next line the postorder traversal sequence of that tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.

Sample Input 1:

7
8 6 5 7 10 8 11

Sample Output 1:

YES
5 7 6 8 11 10 8

Sample Input 2:

7
8 10 11 8 6 7 5

Sample Output 2:

YES
11 8 10 7 5 6 8

Sample Input 3:

7
8 6 8 5 10 9 11

Sample Output 3:

NO

#include<cstdio>
#include<vector>
using namespace std;
struct node{
    int data;
    node *left,*right;
};
vector<int> origin,pre,preM,post,postM;
void insert(node* &root,int data){
    if(root == NULL){
        root = new node;
        root->data = data;
        root->left = root->right =NULL;
        return; 
    }
    if(data < root->data)
        insert(root->left,data);
    else
        insert(root->right,data);
}
void preOrder(node* root,vector<int> &vi){
    if(root == NULL)
        return;
    vi.push_back(root->data);
    preOrder(root->left,vi);
    preOrder(root->right,vi);
}
void preOrderMirror(node* root,vector<int> &vi){
    if(root == NULL)
        return;
    vi.push_back(root->data);
    preOrderMirror(root->right,vi);
    preOrderMirror(root->left,vi);
}
void postOrder(node* root,vector<int> &vi){
    if(root == NULL)
        return;
    postOrder(root->left,vi);
    postOrder(root->right,vi);
    vi.push_back(root->data);
}
void postOrderMirror(node* root,vector<int> &vi){
    if(root == NULL)
        return;
    postOrderMirror(root->right,vi);
    postOrderMirror(root->left,vi);
    vi.push_back(root->data);
}
int main(){
    int n,data;
    node* root =NULL;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&data);
        origin.push_back(data);
        insert(root,data);
    }
    preOrder(root,pre);
    preOrderMirror(root,preM);
    postOrder(root,post);
    postOrderMirror(root,postM);
    if(origin == pre){
        printf("YES\n");
        for(int i = 0;i<post.size();i++){
            printf("%d",post[i]);
            if(i < post.size() - 1)
                printf(" ");
        }
    }else if(origin == preM){
        printf("YES\n");
        for(int i = 0;i<postM.size();i++){
            printf("%d",postM[i]);
            if(i < postM.size() - 1)
                printf(" ");
        }
    }else{
        printf("NO\n");
    } 
    return 0;
}

9.5 平衡二叉树(AVL树)
9.5.1 平衡二叉树的定义
平衡二叉树仍然是一棵二叉查找树，只是在其基础上增加了“平衡”的要求。所谓平衡是指，对AVL树的任意结点来说，其左子树与右子树的高度之差的绝对值不超过1，其中左子树与右子树的高度之差称为该结点的平衡因子。
由于需要对每个结点都得到平衡因子，因此需要在树的结构中加入一个变量height,用来记录以当前结点为根结点的子树的高度：

struct node{
    int v,height;    //v为结点权值，height为当前子树高度 
    node *lchild,*rchild; //左右孩子结点地址 
};

新建一个结点

//生成一个新结点，v为结点权值
node* newNode(int v){
    node* Node = new node;    //申请一个node型变量的地址空间 
    Node->v = v;    //结点权值为v 
    Node->height = 1;    //结点高度初始为1 
    Node->lchild = Node->rchild = NULL;    //初始状态下没有左右孩子 
    return Node;    //返回新建结点的地址 
}

获取结点root所在子树的当前高度：

//获取以root为根结点的子树的当前height
int getHeight(node* root){
    if(root == NULL)
        return 0;
    return root->height;
}

计算平衡因子：

//计算结点root的平衡因子
int getBalanceFactor(node* root){
    //左子树高度减右子树高度
    return getHeight(root->lchild) - getHeight(root->rchild); 
}

9.5.2 平衡二叉树的基本操作

1.查找操作

//search函数查找AVL树中数据域为x的结点 
void search(node* root,int x){
    if(root == NULL){    //空树，查找失败 
        printf("search failed\n");
        return;
    }
    if(x == root->data){    //查找成功，访问之 
        printf("%d\n",root->data);
    }else if(x < root->data){    //如果x比根结点的数据域小，说明x在左子树 
        search(root->lchild,x);
    }else{    //如果x比根结点的数据域大，说明x在右子树 
        search(root->rchild,x);
    }
}

更新结点root的height

//更新结点root的height
void updateHeight(node* root){
    //max(左孩子的height,右孩子的height) + 1
    root->height = max(getHeight(root->lchild),getHeight(root->rchild)) + 1;
}

2.插入操作

左旋步骤：

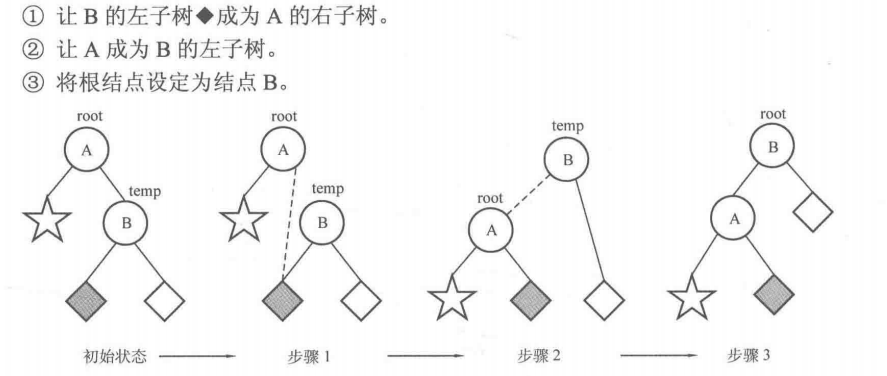
//左旋
void L(node* &root){
    node* temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    updateHeight(root);
    updateHeight(temp);
    root = temp;
}

右旋步骤：

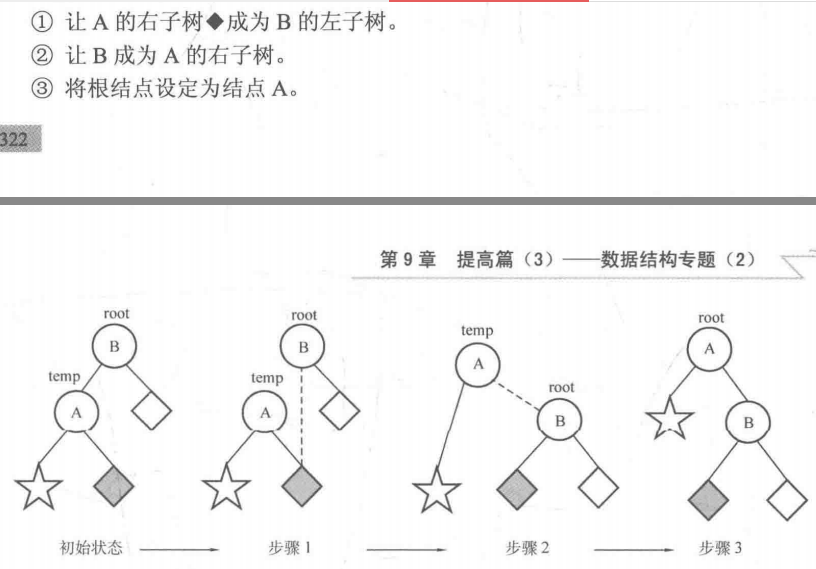
//右旋
void R(node* &root){
    node* temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    updateHeight(root);
    updateHeight(temp);
    root = temp;
}

//插入权值为v的结点 
void insert(node* &root,int v){
    if(root == NULL){ //到达空结点 
        root = newNode(v); 
        return; 
    }
       if(v < root->v){
           insert(root->lchild,v);
        updateHeight(root);
        if(getBalanceFactor(root) == 2){
            if(getBalanceFactor(root->lchild) == 1){
                R(root);
            }else if(getBalanceFactor(root->lchild) == -1){
                L(root->lchild);
                R(root);
            }
        }    
    }else{
        insert(root->rchild,v);
        updateHeight(root);
        if(getBalanceFactor(root) == -2){
            if(getBalanceFactor(root->rchild) == -1){
                L(root);
            }else if(getBalanceFactor(root->rchild) == 1){
                R(root->rchild);
                L(root);
            }
        }
    } 
}

3.AVL树的建立

//AVL树的建立
node* Create(int data[],int n){
    node* root = NULL;
    for(int i=0;i<n;i++){
        insert(root,data[i]);
    }
    return root;
}

9.6 并查集

9.6.1 并查集的定义

并查集支持下面两个操作：

①合并：合并两个集合。

②查找：判断两个元素是否在一个集合。

并查集用一个数组就可以实现： int father[N];

father[i]表示元素i的父亲结点，而父亲结点本身也是这个集合内的元素。例如father[1]=2就表示元素1的父亲结点是元素2。如果father[i] = i，则说明元素i是该集合的根结点。

对同一个集合来说只存在一个根结点，且将其作为所属集合的标识。

9.6.2 并查集的基本操作

1.初始化

一开始，每个元素都是独立的一个集合，因此需要令所有father[i]等于i:

for(int i = 1;i <= N;i++){
    father[i] = i;
}

2.查找

查找操作就是对给定的结点寻找其根结点的过程。实现的方式可以是递推或是递归。

递推的代码：

//findFather函数返回元素x所在集合的根结点 
int findFather(int x){
    while(x != father[x]){
        x = father[x];
    }
    return x;
}

递归：

int findFather(int x){
    if(x == father[x])
        return x;
    else
        return findFather(father[x]);
}

3.合并

合并是指把两个集合合并成一个集合，题目中一般给出两个元素，要求把这两个元素所在的集合合并。

void Union(int a,int b){
    int faA = findFather(a);
    int faB = findFather(b);
    if(faA != faB){
        father[faA] = faB;
    }
}

9.6.3 路径压缩

上面讲解的并查集查找函数是没有经过优化的，在极端情况下效率较低。如果只是为了查找根结点，那么完全可以想办法把操作等价地变成:

father[1] = 1;

father[2] = 1;

father[3] = 1;

对应的变化过程如下图所示:

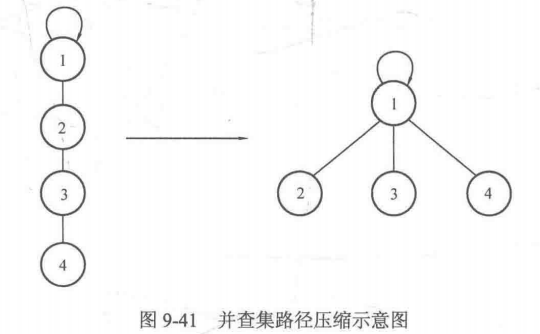
int findFather(int x){
    int a = x;
    while(x != father[x]){
        x = father[x];
    }
    //到这里，x存放的是根结点。下面把路径上的所有结点的father都改成根结点
    while(a != father[a]){
        int z = a;
        a = father[a];
        father[z] = x;
    } 
    return x;
}

#include<cstdio>
const int N = 110;
int father[N];
bool isRoot[N];
int findFather(int x){
    int a = x;
    while(x != father[x]){
        x = father[x];
    }
    while(a != father[a]){
        int z = a;
        a = father[a];
        father[z] = x;
    }
    return x;
}
void Union(int a,int b){
    int faA = findFather(a);
    int faB = findFather(b);
    if(faA != faB){
        father[faA] = faB;
    }
}
void init(int n){
    for(int i = 1;i<=n;i++){
        father[i] = i;
        isRoot[i] = false;
    }
}
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    init(n);
    for(int i=0;i<m;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        Union(a,b);
    }
    int ans = 0;
    for(int i = 1;i<=n;i++){
        isRoot[findFather(i)] = true;
    }
    for(int i=1;i<=n;i++){
        ans += isRoot[i];
    }
    printf("%d\n",ans);
    return 0;
}

9.7 堆

9.7.1 堆的定义与基本操作

堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子结点的值。

//对heap数组在[low,high]范围进行向下调整
//其中low为欲调整结点的数组下标，high一般为堆的最后一个元素的数组下标
void downAdjust(int low,int high){
    int i = low,j = i*2;
    while(j <= high){ //存在孩子结点 
        if(j+1 <= high && heap[j+1] > heap[j]){
            j = j+1; //让j存储右孩子下标 
        }
        //如果孩子中最大的权值比欲调整结点i大 
        if(heap[j] > heap[i]){
            swap(heap[j],heap[i]); //交换最大权值的孩子与欲调整结点i 
            i = j; //保持i为欲调整结点、j为i的左孩子 
            j = i * 2;
        }else{
            break; //孩子的权值均比欲调整结点i小，调整结束 
        }
    }
}

9.8 哈夫曼树

9.8.1 哈夫曼树

带权路径长度：把叶子结点的权值乘以其路径长度。

树的带权路径长度：所有叶子结点的带权路径长度之和。

带权路径长度最小的树被称为哈夫曼树。

合并果子

(fruit.pas/c/cpp)

　　在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过n-1次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

　　因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。
　　例如有3种果子，数目依次为1，2，9。可以先将1、2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为12。
所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。

输入

　　输入包括两行，第一行是一个整数n(1<＝n<=10000)，表示果子的种类数。
　　第二行包含n个整数，用空格分隔，第i个整数ai(1<＝ai<=20000)是第i种果子的数目。

输出

　　输出包括一行，这一行只包含一个整数，也就是最小的体力耗费值。输入数据保证这个值小于2^31。

样例输入

3
1 2 9

样例输出

#include<cstdio>
#include<queue>
using namespace std;
priority_queue<long long,vector<long long>,greater<long long> > q;
int main(){
    int n;
    long long temp,x,y,ans = 0;
    scanf("%d",&n);
    for(int i = 0; i < n;i++){
        scanf("%lld",&temp);
        q.push(temp);
    }
    while(q.size() > 1){
        x = q.top();
        q.pop();
        y = q.top();
        q.pop();
        q.push(x + y);
        ans += x + y;
    }
    printf("%lld\n",ans);
    return 0;
}

posted @ 2020-02-06 18:20 程序员小应阅读(205) 评论(0) 编辑收藏举报

刷新页面返回顶部

程序员小应

算法笔记 第9章 提高篇(3) --数据结构专题(2) 学习笔记

Input Specification:

Output Specification:

Sample Input:

Sample Output:

Input Specification:

Output Specification:

Sample Input 1:

Sample Output 1:

Sample Input 2:

Sample Output 2:

Sample Input 3:

Sample Output 3:

输入

输出

样例输入

样例输出

公告

算法笔记第9章提高篇(3) --数据结构专题(2) 学习笔记