算法笔记 上机训练实战指南 第7章 提高篇(1)--数据结构专题(1) 学习笔记

PAT A1051 Pop Sequence (25分)

Given a stack which can keep M numbers at most. Push N numbers in the order of 1, 2, 3, ..., N and pop randomly. You are supposed to tell if a given sequence of numbers is a possible pop sequence of the stack. For example, if M is 5 and N is 7, we can obtain 1, 2, 3, 4, 5, 6, 7 from the stack, but not 3, 2, 1, 7, 5, 6, 4.

Input Specification:

Each input file contains one test case. For each case, the first line contains 3 numbers (all no more than 1000): M (the maximum capacity of the stack), N (the length of push sequence), and K (the number of pop sequences to be checked). Then K lines follow, each contains a pop sequence of N numbers. All the numbers in a line are separated by a space.

Output Specification:

For each pop sequence, print in one line "YES" if it is indeed a possible pop sequence of the stack, or "NO" if not.

Sample Input:

5 7 5
1 2 3 4 5 6 7
3 2 1 7 5 6 4
7 6 5 4 3 2 1
5 6 4 3 7 2 1
1 7 6 5 4 3 2

Sample Output:

YES
NO
NO
YES
NO
#include<cstdio>
#include<stack>
using namespace std;
stack<int> st;
int main(){
    int m,n,k;
    int arr[1010];
    scanf("%d%d%d",&m,&n,&k);
    while(k--){
        while(!st.empty()){
            st.pop();
        }
        for(int i=1;i<=n;i++){
            scanf("%d",&arr[i]);
        }
        int current = 1;
        bool flag = true;
        for(int i=1;i<=n;i++){
            st.push(i);
            if(st.size() > m){
                flag = false;
                break;
            }
            while(!st.empty() && st.top() == arr[current]){
                st.pop();
                current++;
            }
        }
        if(st.empty() && flag == true){
            printf("YES\n");
        }else{
            printf("NO\n");
        }
    }
    return 0;
}

 PAT A1056 Mice and Rice (25分)

Mice and Rice is the name of a programming contest in which each programmer must write a piece of code to control the movements of a mouse in a given map. The goal of each mouse is to eat as much rice as possible in order to become a FatMouse.

First the playing order is randomly decided for N​P​​ programmers. Then every N​G​​ programmers are grouped in a match. The fattest mouse in a group wins and enters the next turn. All the losers in this turn are ranked the same. Every N​G​​ winners are then grouped in the next match until a final winner is determined.

For the sake of simplicity, assume that the weight of each mouse is fixed once the programmer submits his/her code. Given the weights of all the mice and the initial playing order, you are supposed to output the ranks for the programmers.

Input Specification:

Each input file contains one test case. For each case, the first line contains 2 positive integers: N​P​​ and N​G​​ (≤), the number of programmers and the maximum number of mice in a group, respectively. If there are less than N​G​​ mice at the end of the player's list, then all the mice left will be put into the last group. The second line contains N​P​​ distinct non-negative numbers W​i​​ (,) where each W​i​​ is the weight of the i-th mouse respectively. The third line gives the initial playing order which is a permutation of 0 (assume that the programmers are numbered from 0 to N​P​​−1). All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the final ranks in a line. The i-th number is the rank of the i-th programmer, and all the numbers must be separated by a space, with no extra space at the end of the line.

Sample Input:

11 3
25 18 0 46 37 3 19 22 57 56 10
6 0 8 7 10 5 9 1 4 2 3

Sample Output:

5 5 5 2 5 5 5 3 1 3 5
 
#include<cstdio>
#include<queue>
using namespace std;
const int maxn = 1010;
struct mouse{
    int R;
    int weight;
}mouse[maxn];
int main(){
    int np,ng,order,group;
    scanf("%d%d",&np,&ng);
    for(int i=0;i<np;i++){
        scanf("%d",&mouse[i].weight);
    }
    queue<int> q;
    for(int i=0;i<np;i++){
        scanf("%d",&order);
        q.push(order);
    }
    int temp = np;
    while(q.size()!=1){
        if(temp % ng == 0)
            group = temp/ng;
        else
            group = temp/ng + 1;
        for(int i=0;i<group;i++){
            int k = q.front();
            for(int j=0;j<ng;j++){
                if(i * ng + j >= temp)
                    break;
                int front = q.front();
                if(mouse[front].weight > mouse[k].weight){
                    k = front;
                }
                mouse[front].R = group+1;
                q.pop();
            }
            q.push(k);
        }
        temp = group;
    }
    mouse[q.front()].R = 1;
    for(int i=0;i<np;i++){
        printf("%d",mouse[i].R);
        if(i < np-1)
            printf(" ");
    }
    return 0;
}
1032 Sharing (25分)
 

To store English words, one method is to use linked lists and store a word letter by letter. To save some space, we may let the words share the same sublist if they share the same suffix. For example, loading and being are stored as showed in Figure 1.

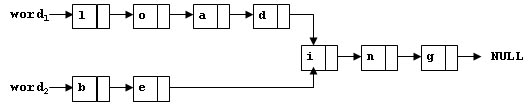
fig.jpg

Figure 1

You are supposed to find the starting position of the common suffix (e.g. the position of i in Figure 1).

Input Specification:

Each input file contains one test case. For each case, the first line contains two addresses of nodes and a positive N (≤), where the two addresses are the addresses of the first nodes of the two words, and N is the total number of nodes. The address of a node is a 5-digit positive integer, and NULL is represented by −.

Then N lines follow, each describes a node in the format:

Address Data Next
 

whereAddress is the position of the node, Data is the letter contained by this node which is an English letter chosen from { a-z, A-Z }, and Next is the position of the next node.

Output Specification:

For each case, simply output the 5-digit starting position of the common suffix. If the two words have no common suffix, output -1 instead.

Sample Input 1:

11111 22222 9
67890 i 00002
00010 a 12345
00003 g -1
12345 D 67890
00002 n 00003
22222 B 23456
11111 L 00001
23456 e 67890
00001 o 00010
 

Sample Output 1:

67890
 

Sample Input 2:

00001 00002 4
00001 a 10001
10001 s -1
00002 a 10002
10002 t -1
 

Sample Output 2:

-1
  
#include<cstdio>
const int maxn = 100010;
struct NODE{
    char data;
    int next;
    int flag;
}node[maxn];
int main(){
    for(int i=0;i<maxn;i++){
        node[i].flag = false;
    }
    int ad1,ad2,n;
    scanf("%d %d %d",&ad1,&ad2,&n);
    int add,data,p;
    for(int i=0;i<n;i++){
        scanf("%d %c %d",&add,&data,&p);
        node[add].data = data;
        node[add].next = p;
    }
    for(p=ad1;p != -1;p=node[p].next){
        node[p].flag = true;
    }
    for(p = ad2; p != -1;p=node[p].next){
        if(node[p].flag == true){
            break;
        }
    }
    if(p!=-1){
        printf("%05d\n",p);
    }else{
        printf("-1\n");
    }
    return 0;
}
PAT A1052 Linked List Sorting (25分)

A linked list consists of a series of structures, which are not necessarily adjacent in memory. We assume that each structure contains an integer key and a Next pointer to the next structure. Now given a linked list, you are supposed to sort the structures according to their key values in increasing order.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive N (<) and an address of the head node, where N is the total number of nodes in memory and the address of a node is a 5-digit positive integer. NULL is represented by −.

Then N lines follow, each describes a node in the format:

Address Key Next
 

where Address is the address of the node in memory, Key is an integer in [−], and Next is the address of the next node. It is guaranteed that all the keys are distinct and there is no cycle in the linked list starting from the head node.

Output Specification:

For each test case, the output format is the same as that of the input, where N is the total number of nodes in the list and all the nodes must be sorted order.

Sample Input:

5 00001
11111 100 -1
00001 0 22222
33333 100000 11111
12345 -1 33333
22222 1000 12345
 

Sample Output:

5 12345
12345 -1 00001
00001 0 11111
11111 100 22222
22222 1000 33333
33333 100000 -1

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 100010;
struct Node{
    int address,data,next;
    bool flag;
}node[maxn];
bool cmp(Node a,Node b){
    if(a.flag==false || b.flag==false){
        return a.flag > b.flag;
    }else{
        return a.data < b.data;
    }
}
int main(){
    for(int i=0;i<maxn;i++){
        node[i].flag = false;
    }
    int n,begin;
    scanf("%d %d",&n,&begin);
    int address;
    for(int i=0;i<n;i++){
        scanf("%d",&address);
        scanf("%d %d",&node[address].data,&node[address].next);
        node[address].address = address;
    }
    int count=0,p = begin;
    while(p != -1){
        node[p].flag = true;
        count++;
        p = node[p].next;
    }
    if(count==0){
        printf("0 -1");
    }else{
        sort(node,node+maxn,cmp);
        printf("%d %05d\n",count,node[0].address);
        for(int i=0;i<count;i++){
            if(i < count-1){
                printf("%05d %d %05d\n",node[i].address,node[i].data,node[i+1].address);
            }else{
                printf("%05d %d -1\n",node[i].address,node[i].data);
            }
        }
    }
    return 0;
}

 

PAT A1097 Deduplication on a Linked List (25分)

Given a singly linked list L with integer keys, you are supposed to remove the nodes with duplicated absolute values of the keys. That is, for each value K, only the first node of which the value or absolute value of its key equals K will be kept. At the mean time, all the removed nodes must be kept in a separate list. For example, given L being 21→-15→-15→-7→15, you must output 21→-15→-7, and the removed list -15→15.

Input Specification:

Each input file contains one test case. For each case, the first line contains the address of the first node, and a positive N (≤) which is the total number of nodes. The address of a node is a 5-digit nonnegative integer, and NULL is represented by −.

Then N lines follow, each describes a node in the format:

Address Key Next

where Address is the position of the node, Key is an integer of which absolute value is no more than 1, and Next is the position of the next node.

Output Specification:

For each case, output the resulting linked list first, then the removed list. Each node occupies a line, and is printed in the same format as in the input.

Sample Input:

00100 5
99999 -7 87654
23854 -15 00000
87654 15 -1
00000 -15 99999
00100 21 23854

Sample Output:

00100 21 23854
23854 -15 99999
99999 -7 -1
00000 -15 87654
87654 15 -1
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 100010;
const int TABLE = 1000010; 
struct Node{
    int address,data,next;
    int order;
}node[maxn];
bool isExist[TABLE] = {false};
bool cmp(Node a,Node b){
    return a.order < b.order;
}
int main(){
    memset(isExist,false,sizeof(isExist));
    for(int i=0;i<maxn;i++){
        node[i].order = 2 * maxn;
    }
    int begin,n;
    scanf("%d%d",&begin,&n);
    int address;
    for(int i=0;i<n;i++){
        scanf("%d",&address);
        scanf("%d %d",&node[address].data,&node[address].next);
        node[address].address = address;
    }    
    int p = begin,countValid=0,countRemoved=0;
    while(p != -1){
        if(!isExist[abs(node[p].data)]){
            isExist[abs(node[p].data)] = true;
            node[p].order = countValid++;
        }else{
            node[p].order =  maxn +countRemoved++;
        }
        p = node[p].next;
    }
    int count = countRemoved + countValid;
    sort(node,node+maxn,cmp);
    for(int i=0;i<count;i++){
        if(i != countValid-1 && i != count -1){
            printf("%05d %d %05d\n",node[i].address,node[i].data,node[i+1].address);
        }else{
            printf("%05d %d -1\n",node[i].address,node[i].data);
        }
    }
    return 0;
}

 



posted @ 2020-02-04 23:00  程序员小应  阅读(166)  评论(0)  编辑  收藏  举报