算法笔记上机训练实战指南第3章入门篇(1)--入门模拟学习笔记 3.1简单模拟

1001 害死人不偿命的(3n+1)猜想 (15分)

卡拉兹(Callatz)猜想：

对任何一个正整数

我们今天的题目不是证明卡拉兹猜想，而是对给定的任一不超过 1000 的正整数

输入格式：

每个测试输入包含 1 个测试用例，即给出正整数

输出格式：

输出从

输入样例：

输出样例：

#include<cstdio>
int main(){
    int n,count=0;
    scanf("%d",&n);
    while(n!=1){
        if(n%2==0){
            n = n/2;
            count++;
        }else{
            n = (3*n+1)/2;
            count++;
        }
    }
    printf("%d",count);
    return 0;
}

1011 A+B 和 C (15分)

给定区间 [ $-] 内的 3 个整数$

输入格式：

输入第 1 行给出正整数

输出格式：

对每组测试用例，在一行中输出 Case #X: true 如果

输入样例：

4
1 2 3
2 3 4
2147483647 0 2147483646
0 -2147483648 -2147483647

输出样例：

Case #1: false
Case #2: true
Case #3: true
Case #4: false

#include<cstdio>
int main(){
    int T,tcase=1;
    scanf("%d",&T);
    while(T--){
        long long a,b,c;
        scanf("%lld%lld%lld",&a,&b,&c);
        if(a+b>c){
            printf("Case #%d: true\n",tcase);
        }else{
            printf("Case #%d: false\n",tcase);
        }
        tcase++;
    }
    return 0;
}

1016 部分A+B (15分)

正整数

现给定

输入格式：

输入在一行中依次给出

输出格式：

在一行中输出

输入样例 1：

3862767 6 13530293 3

输出样例 1：

输入样例 2：

3862767 1 13530293 8

输出样例 2：

#include<cstdio>
#include<cmath>
int main(){
    long long A,B;
    int DA,DB;
    scanf("%lld%d%lld%d",&A,&DA,&B,&DB);
    int PA=0,PB=0; 
    int i=0;
    while(A!=0){
        if(A%10 == DA){
            PA = PA + DA*pow(10,i);
            i++;
        }
        A = A/10;
    }
    i = 0;
    while(B!=0){
        if(B%10 == DB){
            PB = PB + DB*pow(10,i);
            i++;
        }
        B = B/10;
    }
    printf("%d\n",PA+PB);
    return 0;
}

1026 程序运行时间 (15分)

要获得一个 C 语言程序的运行时间，常用的方法是调用头文件 time.h，其中提供了 clock() 函数，可以捕捉从程序开始运行到 clock() 被调用时所耗费的时间。这个时间单位是 clock tick，即“时钟打点”。同时还有一个常数 CLK_TCK，给出了机器时钟每秒所走的时钟打点数。于是为了获得一个函数

这里不妨简单假设常数 CLK_TCK 为 100。现给定被测函数前后两次获得的时钟打点数，请你给出被测函数运行的时间。

输入格式：

输入在一行中顺序给出 2 个整数 C1 和 C2。注意两次获得的时钟打点数肯定不相同，即 C1 $< C2，并且取值在 [。$

输出格式：

在一行中输出被测函数运行的时间。运行时间必须按照 hh:mm:ss（即2位的 时:分:秒）格式输出；不足 1 秒的时间四舍五入到秒。

输入样例：

123 4577973

输出样例：

12:42:59

#include<cstdio>
int main(){
    int c1,c2;
    scanf("%d%d",&c1,&c2);
    int ans = c2-c1;
    if(ans%100>=50){
        ans = ans/100+1;
    }else{
        ans = ans/100;
    }
    printf("%02d:%02d:%02d\n",ans/3600,ans%3600/60,ans%60);
    return 0;
}

1046 划拳 (15分)

划拳是古老中国酒文化的一个有趣的组成部分。酒桌上两人划拳的方法为：每人口中喊出一个数字，同时用手比划出一个数字。如果谁比划出的数字正好等于两人喊出的数字之和，谁就赢了，输家罚一杯酒。两人同赢或两人同输则继续下一轮，直到唯一的赢家出现。

下面给出甲、乙两人的划拳记录，请你统计他们最后分别喝了多少杯酒。

输入格式：

输入第一行先给出一个正整数

甲喊 甲划 乙喊 乙划

其中喊是喊出的数字，划是划出的数字，均为不超过 100 的正整数（两只手一起划）。

输出格式：

在一行中先后输出甲、乙两人喝酒的杯数，其间以一个空格分隔。

输入样例：

输出样例：

1 2

#include<cstdio>
int main(){
    int n;
    scanf("%d",&n);
    int a1,a2,b1,b2;
    int faia=0,faib=0;
    for(int i=0;i<n;i++){
        scanf("%d%d%d%d",&a1,&a2,&b1,&b2);
        if(a1+b1 == a2 && a1+b1 != b2){
            faib++;
        }else if(a1+b1 == b2 && a1+b1 != a2){
            faia++;
        }
    }
    printf("%d %d",faia,faib);
    
    return 0;
}

1008 数组元素循环右移问题 (20分)

一个数组

输入格式:

每个输入包含一个测试用例，第1行输入

输出格式:

在一行中输出循环右移

输入样例:

6 2
1 2 3 4 5 6

输出样例:

5 6 1 2 3 4

#include<cstdio>
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    int a[110];
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
    }
    m = m%n;
    int count=0;
    for(int i=n-m;i<n;i++){
        printf("%d",a[i]);
        count++;
        if(count < n)
            printf(" ");
    }
    for(int i=0;i<n-m;i++){
        printf("%d",a[i]);
        count++;
        if(count < n)
            printf(" ");
    }
    return 0;
}

1012 数字分类 (20分)

给定一系列正整数，请按要求对数字进行分类，并输出以下 5 个数字：

输入格式：

每个输入包含 1 个测试用例。每个测试用例先给出一个不超过 1000 的正整数

输出格式：

对给定的

若其中某一类数字不存在，则在相应位置输出 N。

输入样例 1：

13 1 2 3 4 5 6 7 8 9 10 20 16 18

输出样例 1：

30 11 2 9.7 9

输入样例 2：

8 1 2 4 5 6 7 9 16

输出样例 2：

N 11 2 N 9

#include<cstdio>
int main(){
    int n;
    scanf("%d",&n);
    int count[5] = {0};
    int ans[5] = {0};
    int flag = 1;
    while(n--){
        int temp;
        scanf("%d",&temp);
        if(temp%5 == 0 && temp%2==0){
            ans[0] = ans[0] + temp;
            count[0]++;
        }else if(temp%5 == 1){
            ans[1] = ans[1] + flag*temp;
            flag = -flag;
            count[1]++;
        }else if(temp%5 == 2){
            ans[2]++;
            count[2]++;
        }else if(temp%5 == 3){
            count[3]++;
            ans[3] = ans[3]+temp;
        }else if(temp%5 == 4){
            if(temp > ans[4]){
                ans[4] = temp;
                count[4]++;
            }
        }
    }
    for(int i=0;i<5;i++){
        if(count[i]==0 && i==4){
            printf("N");
            continue;
        }
        if(count[i]==0 && i<4){
            printf("N ");
            continue;
        }
        if(i==3){
            printf("%.1f ",(double)ans[3]/count[3]);
        }else if(i==4){
            printf("%d",ans[i]);
        }else{
            printf("%d ",ans[i]);
        }
    }
    return 0;
}

1018 锤子剪刀布 (20分)

大家应该都会玩“锤子剪刀布”的游戏：两人同时给出手势，胜负规则如图所示：

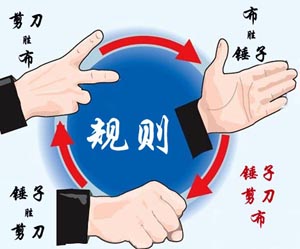
现给出两人的交锋记录，请统计双方的胜、平、负次数，并且给出双方分别出什么手势的胜算最大。

输入格式：

输入第 1 行给出正整数

输出格式：

输出第 1、2 行分别给出甲、乙的胜、平、负次数，数字间以 1 个空格分隔。第 3 行给出两个字母，分别代表甲、乙获胜次数最多的手势，中间有 1 个空格。如果解不唯一，则输出按字母序最小的解。

输入样例：

10
C J
J B
C B
B B
B C
C C
C B
J B
B C
J J

输出样例：

5 3 2
2 3 5
B B

#include<cstdio>
int change(char c){
    if(c=='B'){
        return 0;
    }else if(c == 'C'){
        return 1;
    }else if(c == 'J'){
        return 2;
    }
} 
int main(){
    int n;
    char mp[3]={'B','C','J'};
    scanf("%d",&n);
    char jia,yi;
    int jiacondition[3]={0},yicondition[3]={0};//记录甲乙的胜平负次数
    int handjia[3]={0},handyi[3]={0};//记录甲乙获胜的手势 
    while(n--){
        getchar();
        scanf("%c %c",&jia,&yi);
        int hjia,hyi;
        hjia = change(jia);
        hyi = change(yi);
        if(hjia == hyi){
            jiacondition[1]++;
            yicondition[1]++;
        }else if((hjia+1)%3 == hyi){
            jiacondition[0]++;
            yicondition[2]++;
            handjia[hjia]++;
        }else if((hyi+1)%3 == hjia){
            yicondition[0]++;
            jiacondition[2]++;
            handyi[hyi]++;
        }
    }
    printf("%d %d %d\n",jiacondition[0],jiacondition[1],jiacondition[2]);
    printf("%d %d %d\n",yicondition[0],yicondition[1],yicondition[2]);
    int id1=0,id2=0;
    for(int i=0;i<3;i++){
        if(handjia[i] > handjia[id1]) id1 = i;
        if(handyi[i] > handyi[id2]) id2 = i;
    }
    printf("%c %c",mp[id1],mp[id2]);
    return 0;
}

1046 Shortest Distance (20分)

The task is really simple: given

Input Specification:

Each input file contains one test case. For each case, the first line contains an integer

Output Specification:

For each test case, print your results in

Sample Input:

5 1 2 4 14 9
3
1 3
2 5
4 1

Sample Output:

3
10
7

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 100010;
int dis[MAXN],A[MAXN];
int main(){
    int n;
    int sum=0,query;
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&A[i]);
        sum = sum + A[i];
        dis[i] = sum;
    }
    int left,right;
    scanf("%d",&query);
    for(int i=0;i<query;i++){
        scanf("%d%d",&left,&right);
        if(left >right)
            swap(left,right);
        int temp = dis[right-1]-dis[left-1];
        printf("%d\n",min(temp,sum-temp));
    }
    return 0;
}

1065 A+B and C (64bit) (20分)

Given three integers

Input Specification:

The first line of the input gives the positive number of test cases,

Output Specification:

For each test case, output in one line Case #X: true if

Sample Input:

3
1 2 3
2 3 4
9223372036854775807 -9223372036854775808 0

Sample Output:

Case #1: false
Case #2: true
Case #3: false

#include<cstdio>
int main(){
    int T;
    scanf("%d",&T);
    int i=1;
    while(T--){
        long long A,B,C;
        scanf("%lld%lld%lld",&A,&B,&C);    
        long long res = A+B;
        bool flag;
        if(A > 0 && B>0 && res <0)
            flag = true;
        else if(A < 0 && B < 0 && res>=0)
            flag = false;
        else if(res > C)
            flag = true;
        else 
            flag = false;
        if(flag == true){
            printf("Case #%d: true\n",i++);
        }else{
            printf("Case #%d: false\n",i++);
        }
    }
    return 0;
}

1010 一元多项式求导 (25分)

设计函数求一元多项式的导数。（注：

输入格式:

以指数递降方式输入多项式非零项系数和指数（绝对值均为不超过 1000 的整数）。数字间以空格分隔。

输出格式:

以与输入相同的格式输出导数多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。注意“零多项式”的指数和系数都是 0，但是表示为 0 0。

输入样例:

3 4 -5 2 6 1 -2 0

输出样例:

12 3 -10 1 6 0

#include<cstdio>
int main(){
    int a[1010]={0};
    int e,k,count=0;
    while(scanf("%d%d",&e,&k)!=EOF){
        a[k]=e;
    }
    a[0] = 0;
    for(int i=1;i<=1000;i++){
        a[i-1] = a[i]*i;
        a[i]= 0;
        if(a[i-1]!=0)
            count++;
    }
    if(count==0){
        printf("0 0");
    }else{
        for(int i=1000;i>=0;i--){
            if(a[i]!=0){
                printf("%d %d",a[i],i);
                count--;
                if(count!=0)
                    printf(" ");
            }
        }
    }
    return 0;
}

1002 A+B for Polynomials (25分)

This time, you are supposed to find

Input Specification:

Each input file contains one test case. Each case occupies 2 lines, and each line contains the information of a polynomial:

where

Output Specification:

For each test case you should output the sum of

Sample Input:

2 1 2.4 0 3.2
2 2 1.5 1 0.5

Sample Output:

3 2 1.5 1 2.9 0 3.2

#include<cstdio>
int main(){
    int k;
    scanf("%d",&k);
    double p[1010]={};
    int n;
    double a;
    for(int i=0;i<k;i++){
        scanf("%d %lf",&n,&a);
        p[n] += a;
    }
    scanf("%d",&k);
    for(int i=0;i<k;i++){
        scanf("%d %lf",&n,&a);
        p[n] += a;
    }
    int count=0;
    for(int i=1000;i>=0;i--){
        if(p[i]!=0)
            count++;
    }
    printf("%d",count);
    for(int i=1000;i>=0;i--){
        if(p[i]!=0)
            printf(" %d %.1f",i,p[i]);
    }
    return 0;
}

1009 Product of Polynomials (25分)

This time, you are supposed to find

Input Specification:

Each input file contains one test case. Each case occupies 2 lines, and each line contains the information of a polynomial:

where

Output Specification:

For each test case you should output the product of

Sample Input:

2 1 2.4 0 3.2
2 2 1.5 1 0.5

Sample Output:

3 3 3.6 2 6.0 1 1.6

#include<cstdio>
struct{
    int exp;
    double cof;
}poly[1001];
int main(){
    double ans[2001]={0.0};
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d %lf",&poly[i].exp,&poly[i].cof);
    }
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        int exp;
        double cof;
        scanf("%d %lf",&exp,&cof);
        for(int j=0;j<n;j++){
            ans[exp+poly[j].exp] += (cof*poly[j].cof);    
        }
    }
    int count=0;
    for(int i=0;i<2001;i++){
        if(ans[i]!=0.0)
            count++;
    }
    printf("%d",count);
    for(int i=2000;i>=0;i--){
        if(ans[i]!=0.0)
            printf(" %d %.1f",i,ans[i]);
    }
    return 0;
}

posted @ 2020-01-17 22:42 程序员小应阅读(299) 评论(0) 编辑收藏举报

刷新页面返回顶部

程序员小应

算法笔记 上机训练实战指南 第3章 入门篇(1)--入门模拟 学习笔记 3.1简单模拟

输入格式：

输出格式：

输入样例：

输出样例：

输入格式：

输出格式：

输入样例：

输出样例：

输入格式：

输出格式：

输入样例 1：

输出样例 1：

输入样例 2：

输出样例 2：

输入格式：

输出格式：

输入样例：

输出样例：

输入格式：

输出格式：

输入样例：

输出样例：

输入格式:

输出格式:

输入样例:

输出样例:

输入格式：

输出格式：

输入样例 1：

输出样例 1：

输入样例 2：

输出样例 2：

输入格式：

输出格式：

输入样例：

输出样例：

Input Specification:

Output Specification:

Sample Input:

Sample Output:

Input Specification:

Output Specification:

Sample Input:

Sample Output:

输入格式:

输出格式:

输入样例:

输出样例:

Input Specification:

Output Specification:

Sample Input:

Sample Output:

Input Specification:

Output Specification:

Sample Input:

Sample Output:

公告

算法笔记上机训练实战指南第3章入门篇(1)--入门模拟学习笔记 3.1简单模拟