自然语言处理入门 何晗 读书笔记 第2章 词典分词
中文分词指的是将一段文本拆分为一系列单词的过程,这些单词顺序拼接后等于原文本。中文分词算法大致分为基于词典规则与基于机器学习这两大派别。本章先从简单的规则入手,为读者介绍一些高效的词典匹配算法。
词典分词 是最简单、最常见的分词算法,仅需一部词典和一套查词典的规则即可,适合初学者入门。给定一部词典,词典分词就是一个确定的查词与输出的规则系统。词典分词的重点不在于分词本身,而在于支撑词典的数据结构。
本章先介绍词的定义与性质,然后给出一部词典。
2.1 什么是词
2.1.1 词的定义
在基于词典的中文分词中,词的定义要现实得多:词典中的字符串就是词。根据此定义,词典之外的字符串就不是词了。这个推论或许不符合读者的期望,但这就是词典分词故有的弱点。事实上,语言中的词汇数量是无穷的,无法用任何词典完整收录,
2.1.2 词的性质----齐夫定律
齐夫定律:一个单词的词频与它的词频排名成反比。就是说,虽然存在很多生词,但生词的词频较小,趋近于0,平时很难碰到。至少在常见的单词的切分上,可以放心地试一试词典分词。
实现词典分词的第一个步骤,当然是准备一份词典了。
2.2 词典
互联网上有许多公开的中文词库,
比如搜狗实验室发布的互联网词库(SogouW,其中有15万个词条) https://www.sogou.com/labs/resource/w.php,
清华大学开放中文词库(THUOCL),http://thunlp.org
何晗发布的千万级巨型汉语词库(千万级词条):http://www.hankcs.com/nlp/corpus/tens-of-millions-of-giant-chinese-word-library-share.html
2.2.1 HanLP词典
CoreNatureDictionary.mini.txt文件

第一列是单词本身,之后每两列分别表示词性与相应的词频。希望这个词以动词出现了386次,以名词的身份出现了96次。
2.2.2 词典的加载
利用HanLP,读取CoreNatureDictionary.mini.txt文件,只需一行代码
TreeMap<String, CoreDictionary.Attribute> dictionary =
IOUtil.loadDictionary("data/dictionary/CoreNatureDictionary.mini.txt");
得了一个TreeMap,它的键宿舍单词本身,而值是CoreDictionary.Attribute
查看这份词典的大小,以及按照字典序排列的第一个单词:
System.out.printf("词典大小:%d个词条\n", dictionary.size());
System.out.println(dictionary.keySet().iterator().next());

2.3 切分算法
2.3.1 完全切分
完全切分指的是,找出一段文本中的所有单词。朴素的完全切分算法其实非常简单,只要遍历文本中的连续序列,查询该序列是否在词典中即可。定义词典为dic,文本为text,当前的处理位置为i,完全切分的python算法如下:
def fully_segment(text, dic): word_list = [] for i in range(len(text)): # i 从 0 到text的最后一个字的下标遍历 for j in range(i + 1, len(text) + 1): # j 遍历[i + 1, len(text)]区间 word = text[i:j] # 取出连续区间[i, j]对应的字符串 if word in dic: # 如果在词典中,则认为是一个词 word_list.append(word) return word_list
代码详见tests/book/ch02/fully_segment.py
主函数
if __name__ == '__main__': dic = load_dictionary() print(fully_segment('商品和服务', dic))
运行结果:

Java代码
/** * 完全切分式的中文分词算法 * * @param text 待分词的文本 * @param dictionary 词典 * @return 单词列表 */ public static List<String> segmentFully(String text, Map<String, CoreDictionary.Attribute> dictionary) { List<String> wordList = new LinkedList<String>(); for (int i = 0; i < text.length(); ++i) { for (int j = i + 1; j <= text.length(); ++j) { String word = text.substring(i, j); if (dictionary.containsKey(word)) { wordList.add(word); } } } return wordList; }
// 完全切分
System.out.println(segmentFully("就读北京大学", dictionary));
结果:

2.3.2 正向最长匹配
完全切分的结果比较没有意义,我们更需要那种有意义的词语序列,而不是所有出现在词典中的单词所构成的链表。 所以需要完善一下处理规则,考虑到越长的单词表达的意义越丰富,于是我们定义单词越长优先级越高。具体说来,就是在以某个下标为起点递增查词的过程中,优先输出更长的单词,这种规则被称为最长匹配算法。扫描顺序从前往后,则称为正向最长匹配,反之则为逆向最长匹配。
Python代码
def forward_segment(text, dic): word_list = [] i = 0 while i < len(text): longest_word = text[i] # 当前扫描位置的单字 for j in range(i + 1, len(text) + 1): # 所有可能的结尾 word = text[i:j] # 从当前位置到结尾的连续字符串 if word in dic: # 在词典中 if len(word) > len(longest_word): # 并且更长 longest_word = word # 则更优先输出 word_list.append(longest_word) # 输出最长词 i += len(longest_word) # 正向扫描 return word_list
调用
if __name__ == '__main__': dic = load_dictionary() print(forward_segment('就读北京大学', dic)) print(forward_segment('研究生命起源', dic))

Java代码
/** * 正向最长匹配的中文分词算法 * * @param text 待分词的文本 * @param dictionary 词典 * @return 单词列表 */ public static List<String> segmentForwardLongest(String text, Map<String, CoreDictionary.Attribute> dictionary) { List<String> wordList = new LinkedList<String>(); for (int i = 0; i < text.length(); ) { String longestWord = text.substring(i, i + 1); for (int j = i + 1; j <= text.length(); ++j) { String word = text.substring(i, j); if (dictionary.containsKey(word)) { if (word.length() > longestWord.length()) { longestWord = word; } } } wordList.add(longestWord); i += longestWord.length(); } return wordList; }

2.3.3 逆向最长匹配
Python代码
def backward_segment(text, dic): word_list = [] i = len(text) - 1 while i >= 0: # 扫描位置作为终点 longest_word = text[i] # 扫描位置的单字 for j in range(0, i): # 遍历[0, i]区间作为待查询词语的起点 word = text[j: i + 1] # 取出[j, i]区间作为待查询单词 if word in dic: if len(word) > len(longest_word): # 越长优先级越高 longest_word = word word_list.insert(0, longest_word) # 逆向扫描,所以越先查出的单词在位置上越靠后 i -= len(longest_word) return word_list
Java代码
/** * 逆向最长匹配的中文分词算法 * * @param text 待分词的文本 * @param dictionary 词典 * @return 单词列表 */ public static List<String> segmentBackwardLongest(String text, Map<String, CoreDictionary.Attribute> dictionary) { List<String> wordList = new LinkedList<String>(); for (int i = text.length() - 1; i >= 0; ) { String longestWord = text.substring(i, i + 1); for (int j = 0; j <= i; ++j) { String word = text.substring(j, i + 1); if (dictionary.containsKey(word)) { if (word.length() > longestWord.length()) { longestWord = word; } } } wordList.add(0, longestWord); i -= longestWord.length(); } return wordList; }

结果还是出现问题,因此有人提出综合两种规则,期待它们取长补短,称为双向最长匹配。
2.3.4 双向最长匹配
统计显示,正向匹配错误而逆向匹配正确的句子占9.24%。
双向最长匹配规则集,流程如下:
(1)同时执行正向和逆向最长匹配,若两者的词数不同,则返回词数更少的那一个。
(2)否则,返回两者中单字更少的那一个。当单字数也相同时,优先返回逆向最长匹配的结果。
Python代码
from backward_segment import backward_segment
from forward_segment import forward_segment
from utility import load_dictionary
def count_single_char(word_list: list): # 统计单字成词的个数
return sum(1 for word in word_list if len(word) == 1)
def bidirectional_segment(text, dic):
f = forward_segment(text, dic)
b = backward_segment(text, dic)
if len(f) < len(b): # 词数更少优先级更高
return f
elif len(f) > len(b):
return b
else:
if count_single_char(f) < count_single_char(b): # 单字更少优先级更高
return f
else:
return b # 都相等时逆向匹配优先级更高
if __name__ == '__main__':
dic = load_dictionary()
print(bidirectional_segment('研究生命起源', dic))
Java版本
/** * 双向最长匹配的中文分词算法 * * @param text 待分词的文本 * @param dictionary 词典 * @return 单词列表 */ public static List<String> segmentBidirectional(String text, Map<String, CoreDictionary.Attribute> dictionary) { List<String> forwardLongest = segmentForwardLongest(text, dictionary); List<String> backwardLongest = segmentBackwardLongest(text, dictionary); if (forwardLongest.size() < backwardLongest.size()) return forwardLongest; else if (forwardLongest.size() > backwardLongest.size()) return backwardLongest; else { if (countSingleChar(forwardLongest) < countSingleChar(backwardLongest)) return forwardLongest; else return backwardLongest; } }
主函数调用部分代码
// 双向最长匹配 String[] text = new String[]{ "项目的研究", "商品和服务", "研究生命起源", "当下雨天地面积水", "结婚的和尚未结婚的", "欢迎新老师生前来就餐", }; for (int i = 0; i < text.length; i++) { System.out.printf("| %d | %s | %s | %s | %s |\n", i + 1, text[i], segmentForwardLongest(text[i], dictionary), segmentBackwardLongest(text[i], dictionary), segmentBidirectional(text[i], dictionary) ); }

比较之后发现,双向最长匹配在2、3、5这3种情况下选择出了最好的结果,但在4号句子上选择了错误的结果,使得最终正确率3/6反而小于逆向最长匹配的4/6。由此,规则系统的脆弱可见一斑。规则集的维护有时是拆东墙补西墙,有时是帮倒忙。
2.3.5 速度评测
词典分词的规则没有技术含量,消除歧义的效果不好。词典分词的核心价值不在于精度,而在于速度。
Python
def evaluate_speed(segment, text, dic): start_time = time.time() for i in range(pressure): segment(text, dic) elapsed_time = time.time() - start_time print('%.2f 万字/秒' % (len(text) * pressure / 10000 / elapsed_time)) if __name__ == '__main__': text = "江西鄱阳湖干枯,中国最大淡水湖变成大草原" pressure = 10000 dic = load_dictionary() print('由于JPype调用开销巨大,以下速度显著慢于原生Java') evaluate_speed(forward_segment, text, dic) evaluate_speed(backward_segment, text, dic) evaluate_speed(bidirectional_segment, text, dic)

Java
public static void evaluateSpeed(Map<String, CoreDictionary.Attribute> dictionary) { String text = "江西鄱阳湖干枯,中国最大淡水湖变成大草原"; long start; double costTime; final int pressure = 10000; System.out.println("正向最长"); start = System.currentTimeMillis(); for (int i = 0; i < pressure; ++i) { segmentForwardLongest(text, dictionary); } costTime = (System.currentTimeMillis() - start) / (double) 1000; System.out.printf("%.2f万字/秒\n", text.length() * pressure / 10000 / costTime); System.out.println("逆向最长"); start = System.currentTimeMillis(); for (int i = 0; i < pressure; ++i) { segmentBackwardLongest(text, dictionary); } costTime = (System.currentTimeMillis() - start) / (double) 1000; System.out.printf("%.2f万字/秒\n", text.length() * pressure / 10000 / costTime); System.out.println("双向最长"); start = System.currentTimeMillis(); for (int i = 0; i < pressure; ++i) { segmentBidirectional(text, dictionary); } costTime = (System.currentTimeMillis() - start) / (double) 1000; System.out.printf("%.2f万字/秒\n", text.length() * pressure / 10000 / costTime); }

总结:
1、Python的运行速度比Java慢,效率只有Java的一半不到
2、正向匹配与逆向匹配的速度差不多,是双向的两倍。因为双向做了两倍的工作
3、Java实现的正向匹配比逆向匹配快。
2.4 字典树
2.4.1 什么是字典树
字符串集合常用字典树存储,这是一种字符串上的树形数据结构。字典树中每条边都对应一个字,从根节点往下的路径构成一个个字符串。字典树并不直接在节点上存储字符串,而是将词语视作根节点到某节点之间的一条路径,并在终点节点上做个标记"该节点对应词语的结尾".字符串就是一条路径,要查询一个单词,只需顺着这条路径从根节点往下走。如果能走到特殊标记的节点,则说明该字符串在集合中,否则说明不存在。
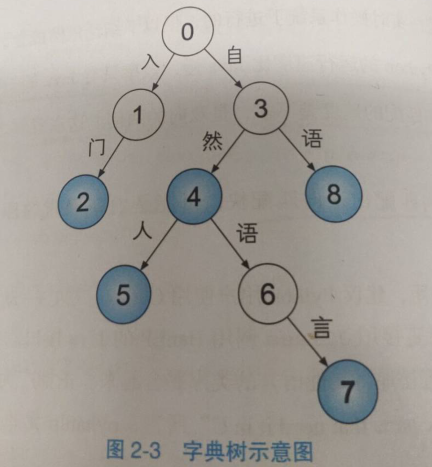
蓝色标记着该节点是一个词的结尾,数字是人为的编号。这棵树中存储的词典如下所示:
入门: 0--1--2
自然: 0--3--4
自然人: 0--3--4--5
2.4.2 字典树的节点实现
约定用值为None表示节点不对应词语,虽然这样就不能插入值为None的键了,但实现起来更简单。
节点的Python描述如下:
class Node(object): def __init__(self, value) -> None: self._children = {} self._value = value def _add_child(self, char, value, overwrite=False): child = self._children.get(char) if child is None: child = Node(value) self._children[char] = child elif overwrite: child._value = value return child
2.4.3 字典树的增删改查实现
"删改查"其实是一回事,都是查询。删除操作就是将终点的值设为None而已,修改操作无非是将它的值设为另一个值而已。
从确定有限状态自动机的角度来讲,每个节点都是一个状态,状态表示当前已查询到的前缀。
状态 前缀
0 “(空白)
1 入
2 入门
。。。。
从父节点到子节点的移动过程可以看作一次状态转移。
”增加键值对“其实还是查询,只不过在状态转移失败的时候,则创建相应的子节点,保证转移成功。
字典树的完整实现如下:
class Trie(Node): def __init__(self) -> None: super().__init__(None) def __contains__(self, key): return self[key] is not None def __getitem__(self, key): state = self for char in key: state = state._children.get(char) if state is None: return None return state._value def __setitem__(self, key, value): state = self for i, char in enumerate(key): if i < len(key) - 1: state = state._add_child(char, None, False) else: state = state._add_child(char, value, True)
写一些测试:
if __name__ == '__main__': trie = Trie() # 增 trie['自然'] = 'nature' trie['自然人'] = 'human' trie['自然语言'] = 'language' trie['自语'] = 'talk to oneself' trie['入门'] = 'introduction' assert '自然' in trie # 删 trie['自然'] = None assert '自然' not in trie # 改 trie['自然语言'] = 'human language' assert trie['自然语言'] == 'human language' # 查 assert trie['入门'] == 'introduction'
2.4.4 首字散列其余二分的字典树
读者也许听说过散列函数,它用来将对象转换为整数。散列函数必须满足的基本要求是:对象相同,散列值必须相同。散列函数设计不当,则散列表的内存效率和查找效率都不高。Python没有char类型,字符被视作长度为1的字符串,所以实际调用的就是str的散列函数。在64位系统上,str的散列函数返回64位的整数。但Unicode字符总共也才136690个,远远小于2^64。这导致两个字符在字符集中明明相邻,然而散列值却相差万里。
Java中的字符散列函数则要友好一些,Java中字符的编码为UTF-16。每个字符都可以映射为16位不重复的连续整数,恰好是完美散列。这个完美的散列函数输出的是区间[0,65535]内的正整数,用来索引子节点非常合适。具体做法是创建一个长为65536的数组,将子节点按对应的字符整型值作为下标放入该数组中即可。这样每次状态转移时,只需访问对应下标就行了,这在任何编程语言中都是极快的。然而这种待遇无法让每个节点都享受,如果词典中的词语最长为l,则最坏情况下字典树第l层的数组容量之和为O(65536^l)。内存指数膨胀,不现实。一个变通的方法是仅在根节点实施散列策略。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号