PAT 1049 Counting Ones (30分) 编程之美--1的个数

题目

The task is simple: given any positive integer N, you are supposed to count the total number of 1's in the decimal form of the integers from 1 to N. For example, given N being 12, there are five 1's in 1, 10, 11, and 12.

Input Specification:
Each input file contains one test case which gives the positive N (≤2^​30​​ ).

Output Specification:
For each test case, print the number of 1's in one line.

Sample Input:

12

Sample Output:

5

解析

题意：

给定一个正整数N，求从1-N的所有正整数中，1总共出现了几次。

思路：

这道题是《编程之美》上面的一道题（第2.4节），需要通过分析来总结规律，然后总结出公式，如果暴力去“数”1的个数，显然会超时。但如果通过公式来算的话，时间复杂度就直接降到O(1)。具体分析过程比较复杂，详情参见《编程之美》2.4节“1的数目”，这里只给出结论——从右往左拆解当前数字，逐位分析每个位置出现1的次数，然后统计其规律与当前位置左右部分数字的关系，最后累加，即为结果。

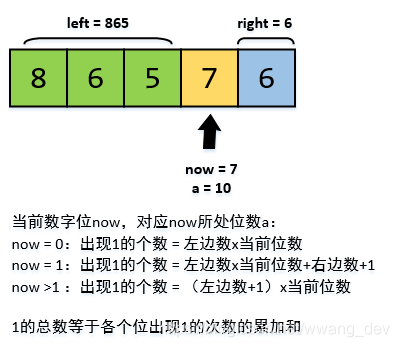
以数字N=345、N=305、N=315为例，寻找十位上是1的数字个数。将数字分成3部分：百位、十位、个位。

• 当N=345时，从1-345这345个数中，百位数字可以出现0、1、2、3四种，每种百位数字都可以跟一个数字为1的十位，而每种十位数字可以跟0-9这十种数字，所以从1~345这345个数中，十位数字为1的数共有(3+1)×10=40个，故十位上的1共出现40次。
• 当N=305时，百位上数字依然可以出现0、1、2、3四种，但要注意，百位数字为3时，后面不能再跟数字为1的十位，因为这样的数字已经大于305了，所以从1~305这305个数中，十位数字为1的数共有3×10=30个，故十位上的1共出现30次。
• 当N=315时，百位上数字依然可以出现0、1、2、3四种，此时要注意，百位数字为3时，后面可以再跟数字为1的十位，但这样的数字个位上只能出现0-5这6个数，即310、311、312、313、314、315，其他数字都会大于315，所以从1~315这315个数中，十位数字为1的数共有3×10+(5+1)=36个，故十位上的1共出现36次。

综上，对于任意一个数字N，当要判断从右向左数第i位上1出现的次数num时，可以将这个数字分成三部分，分别用left、current、right表示，即left=数字N在i位左侧的数字、current=数字N在第i位的数字、right=数字N在i位右侧的数字。例如数字N=123456，判断从右向左第3位也就是百位上，即数字4所在位置1出现的次数时，left=123、current=4、right=56。此时分三种情况进行计算：

• current=0：num = left × 10ⁱ

• current=1：num = left × 10ⁱ+ (right + 1)

• current>1：num = (left + 1) × 10ⁱ

• 其中10^i^就表示的是当前处理的是个位、十位、还是百位、千位.......

所以如果使用result存储最后的答案，用a表示当前是个、十、百、千位……使用left表示左边部分表示的数字，right表示右边部分表示的数字。

则从右往左（从个位往高位）开始遍历，判断当前位置的字符：

• 若是0：则在当前位置可以出现1的次数为left * a次。

• 若是1：则在当前位置可以出现1的次数为left * a + right + 1次

• 其他（2-9）：则在当前位置出现1 的次数为(left+1)*a

代码

#include <iostream>
using namespace std;

int main() {
    int n, ans = 0, radix = 1, left, right, curr;
    cin >> n;
    while (n / radix) {
        left = n / (radix * 10); curr = n / radix % 10; right = n % radix;
        if (curr == 0) ans += left * radix;
        else if (curr == 1) ans += left * radix + right + 1;
        else ans += (left + 1) * radix;
        radix *= 10;
    } 
    cout << ans;
    return 0;
}