图像卷积
在上一篇文章中，我们了解了卷积的原理，下面让我们来看看卷积在图像识别中的具体操作
互相关运算
严格来说，卷积层是一个错误的叫法，因为它表达的运算其实是数学上的互相关（cross-correlation）运算，而不是卷积运算
我们先来看一下二维图像的互相关运算：
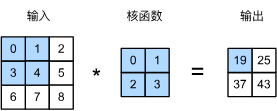
在二维互相关运算中，卷积窗口从输入张量的左上角开始，从左到右、从上到下滑动。 当卷积窗口滑动到新一个位置时，包含在该窗口中的部分张量与卷积核张量进行按元素相乘，得到的张量再求和得到一个单一的标量值，由此我们得出了这一位置的输出张量值。 在如上例子中，输出张量的四个元素由二维互相关运算得到，这个输出高度为2、宽度为2，如下所示：
注意，输出大小略小于输入大小。这是因为卷积核的宽度和高度大于1， 而卷积核只与图像中每个大小完全适合的位置进行互相关运算。 所以，输出大小等于输入大小\(n_h \times n_w\)减去卷积核大小\(k_h \times k_w\)，即：
这是因为我们需要足够的空间在图像上“移动”卷积核。稍后，我们将看到如何通过在图像边界周围填充零来保证有足够的空间移动卷积核，从而保持输出大小不变。 接下来，我们在corr2d函数中实现如上过程，该函数接受输入张量X和卷积核张量K，并返回输出张量Y。
import torch
from torch import nn
from d2l import torch as d2l
def corr2d(X, K): #@save
"""计算二维互相关运算"""
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
return Y
卷积层
卷积层对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出。 所以，卷积层中的两个被训练的参数是卷积核权重和标量偏置。 就像我们之前随机初始化全连接层一样，在训练基于卷积层的模型时，我们也随机初始化卷积核权重。
基于上面定义的corr2d函数实现二维卷积层。在__init__构造函数中，将weight和bias声明为两个模型参数。前向传播函数调用corr2d函数并添加偏置。
class Conv2D(nn.Module):
def __init__(self, kernel_size):
super().__init__()
self.weight = nn.Parameter(torch.rand(kernel_size))
self.bias = nn.Parameter(torch.zeros(1))
def forward(self, x):
return corr2d(x, self.weight) + self.bias
学习卷积核
我们知道不同的卷积核能够识别图像的不同特征，然而，我们不可能手动的去设计卷积核。那么我们是否可以学习由X生成Y的卷积核呢？
现在让我们看看是否可以通过仅查看“输入-输出”对来学习由X生成Y的卷积核。 我们先构造一个卷积层，并将其卷积核初始化为随机张量。接下来，在每次迭代中，我们比较Y与卷积层输出的平方误差，然后计算梯度来更新卷积核。为了简单起见，我们在此使用内置的二维卷积层，并忽略偏置。
# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)
# 这个二维卷积层使用四维输入和输出格式（批量大小、通道、高度、宽度），
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2 # 学习率
for i in range(10):
Y_hat = conv2d(X)
# 这里使用L2范数计算损失
l = (Y_hat - Y) ** 2
# 首先梯度清零
conv2d.zero_grad()
# 计算损失并反向传播计算梯度
l.sum().backward()
# 迭代卷积核
conv2d.weight.data[:] -= lr * conv2d.weight.grad
if (i + 1) % 2 == 0:
print(f'epoch {i+1}, loss {l.sum():.3f}')
结果：
epoch 2, loss 6.422
epoch 4, loss 1.225
epoch 6, loss 0.266
epoch 8, loss 0.070
epoch 10, loss 0.022
在10次迭代之后，误差已经降到足够低。现在我们来看看我们所学的卷积核的权重张量。
conv2d.weight.data.reshape((1, 2))
tensor([[ 1.0010, -0.9739]])
特征映射和感受野
输出的卷积层有时被称为特征映射（feature map），因为它可以被视为一个输入映射到下一层的空间维度的转换器。 在卷积神经网络中，对于某一层的任意元素x，其感受野（receptive field）是指在前向传播期间可能影响计算的所有元素（来自所有先前层）。
请注意，感受野可能大于输入的实际大小。让我们用 图6.2.1为例来解释感受野： 给定\(2 \times 2\)卷积核，阴影输出元素值19的感受野是输入阴影部分的四个元素。 假设之前输出为\(Y\)，其大小为\(2\times2\)，现在我们在其后附加一个卷积层，该卷积层以\(Y\)为输入，输出单个元素\(z\)。 在这种情况下，\(Y\)上的\(z\)的感受野包括\(Y\)的所有四个元素，而输入的感受野包括最初所有九个输入元素。 因此，当一个特征图中的任意元素需要检测更广区域的输入特征时，我们可以构建一个更深的网络。
总结
所谓的卷积其本质上就是利用数学上的互相关运算对图像的某个特征进行提取，而一个卷积神经网络可以由多个卷积核提取图像的不同的特征，而这些卷积核并不是人为设计的，而是利用了神经网络的梯度下降和反向传播不断的进行学习的。
