一、实现思想
图的邻接矩阵表示法，也叫数组表示法。用一个一维数组存储图中的顶点，用一个二维数组存储图中的边，即各个顶点直接的边的关系，这个二维数组就叫「邻接矩阵」。
不用代码的话，我们都比较熟悉，图的深度遍历和广度遍历。但是用代码怎么实现，这就要考虑存储一个图了，这个正是本博客的重点。
设图G=(V,E),有n个顶点，则邻接矩阵是一个 n X n的二维数组。V代表一个点集，E代表一个边集。
- 对于非网图(没有权值的有向、无向图)
= = 1 若(vi,vj) 属于 E
edge[i][j]
= = 0 否则
这条公式很精辟，因为概括地很好，既包括了有向图，也包括了无向图。其实本质上，我们在置1的时候，考虑的是连通性，如果某个点可以到另一个点，那么二维数组的某个位置就可以置1了。
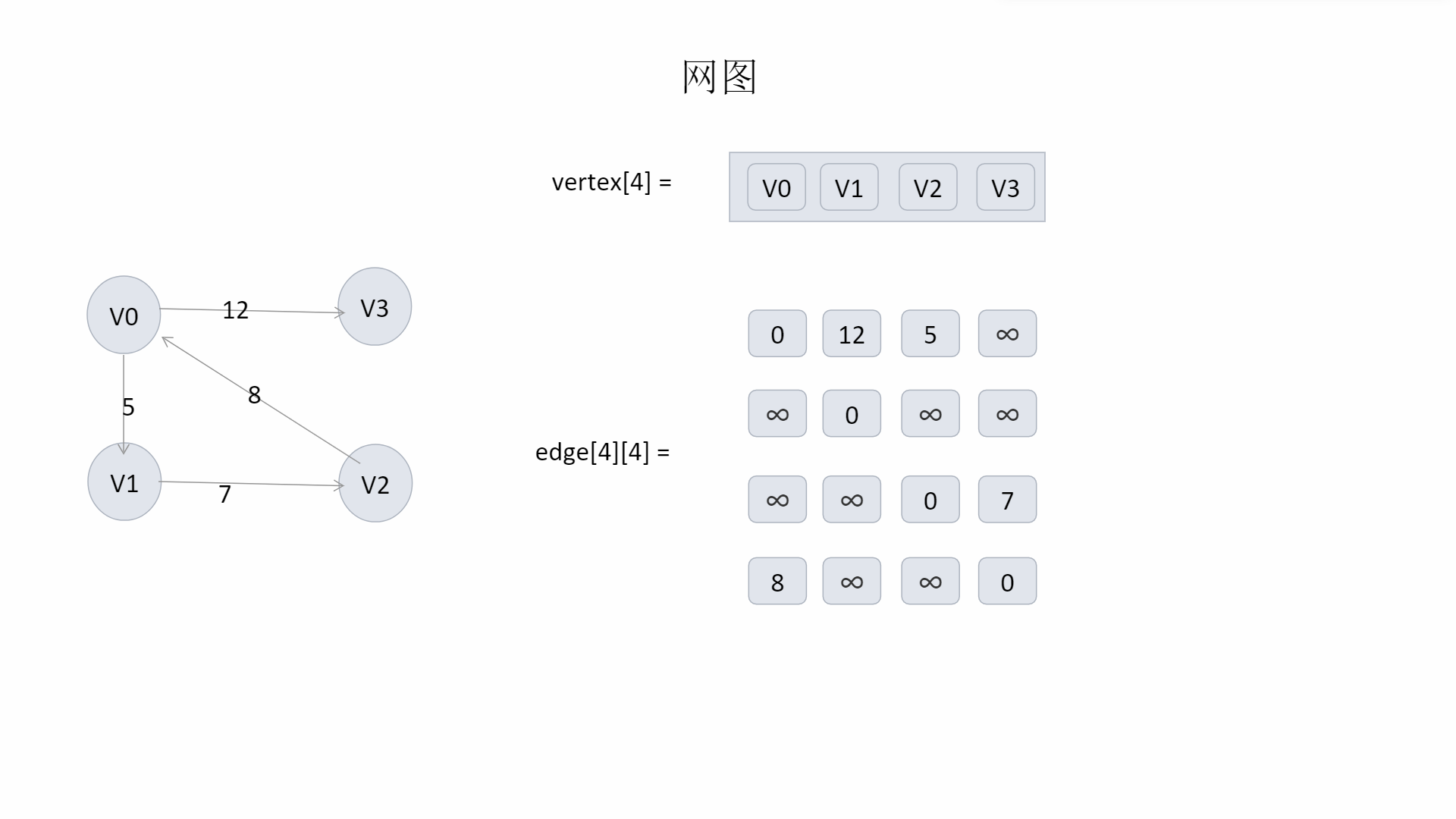
- 对于网图(有权值的有向、无向图)
= w(ij) 若(vi,vj)属于 E。w(ij)代表某条边的权值
edge[i][j] = 0 若 i = j
= ∞ 否则
二、实现图
这里以无向图，不带权值为例子
- 无向图的深度遍历
- 从二维数组的角度来看，我觉得深度遍历的妙处在于，会跳下去。找到一个点之后，顺着这个点往下跳。
- 里面用到了递归，跳不下去了，就开始返回。
- 无向图的广度遍历
- 里面用到了「队列」
- 从二维数组的角度来看，找到某一行之后，我就扫描完这一行再走。根据队列再找下一行。
代码实现
这个代码是无向非网图的例子。
- 类的结构
const int MaxSize = 10;//简单起见，矩阵不要太大
int visited[MaxSize];//记录点是否被访问过
template <typename DataType>
class MGraphy
{
public:
MGraphy(DataType a[], int n, int e); //构造函数
~MGraphy();
void DFTraverse(int v); //深度搜索
void BFTraverse(int v); //广度搜索
private:
DataType vertex[MaxSize]; //存放点的数组
int edge[MaxSize][MaxSize]; //存放图的二维数组
int vertexNum, edgeNum; //图的顶点数和边数
};
- 构造函数
template <typename DataType>
MGraphy<DataType>::MGraphy(DataType a[], int n, int e)
{
vertexNum = n;
edgeNum = e;
for (int i = 0; i < vertexNum; i++) //存储顶点
vertex[i] = a[i];
for (int i = 0; i < vertexNum; i++) //初始化邻接矩阵，即二维数组
for (int j = 0; j < vertexNum; j++)
edge[i][j] = 0;
for (int i = 0; i < MaxSize; i++) //初始化访问标志数组
visited[i] = 0;
for (int i = 0; i < edgeNum; i++) //依次输入每一条边
{
int m, n;
cin >> m >> n; //输入边依附的两个顶点的编号
edge[m][n] = 1; //置边标志
edge[n][m] = 1;
}
}
- 深搜
template <typename DataType>
void MGraphy<DataType>::DFTraverse(int v)
{
cout << vertex[v];
visited[v] = 1;
for (int i = 0; i < vertexNum; i++)
if (edge[v][i] == 1 && visited[i] == 0)
DFTraverse(i); //找到一个点就跳下去
}
- 广搜
template <typename DataType>
void MGraphy<DataType>::BFTraverse(int v)
{
int Q[MaxSize];
int front = -1, rear = -1;
cout << vertex[v];
visited[v] = 1;
Q[++rear] = v;
while (front != rear)
{
int w = Q[++front]; //将队头元素出队，并送到w中
for (int i = 0; i < vertexNum; i++) //对二维数组而言，就是扫描完一行再走
{
if (edge[w][i] == 1 && visited[i] == 0)
{
cout << vertex[i];
visited[i] = 1;
Q[++rear] = i;
}
}
}
}
- Main函数做测试
int main(void)
{
string Name[4] = {"a", "b", "c", "d"};
MGraphy<string> *gra = new MGraphy<string>(Name, 4, 4);
gra->DFTraverse(0);
for (int i = 0; i < MaxSize; i++) //初始化访问标志数组
visited[i] = 0;
printf("\n");
gra->BFTraverse(0);
return 0;
}
/*
输入:
0 3
0 1
1 3
1 2
输出
abcd
abdc
*/
四、总结
- 这个是我看 王红梅数据结构做的笔记
- 这是第一次用代码，基于邻接表，实现图的存储与遍历。不算很难，但是奇妙的也很好
