查找：二叉查找树 c++ 2020年8月

一、实现思想

　　1、二叉查找树，实际上是根据『左小右大』的规则去生成一颗二叉树。

　　2、这就有点类似折半查找，可以瞬间排除一大部分数据，专注于树的一边。

　　3、最有趣的是，『左小右大』生成的树，中序遍历后得到的数据居然是有序的(这个和查找没有什么关系，但是真的很妙)

补充：

　　1、我觉得构建一棵树并不难，最难的是对这棵树进行删除操作，因为需要调整树的结构，所以第二部分图列会专注于删除。

　　2、为了便于实现删除操作，我为节点增加了指向父节点的指针。

1 typedef struct NODE
2 {
3     int data;
4     NODE *left;
5     NODE *right;
6     NODE *parent;
7 } Node, *pNode;

二、实现图例

1、构建一棵树

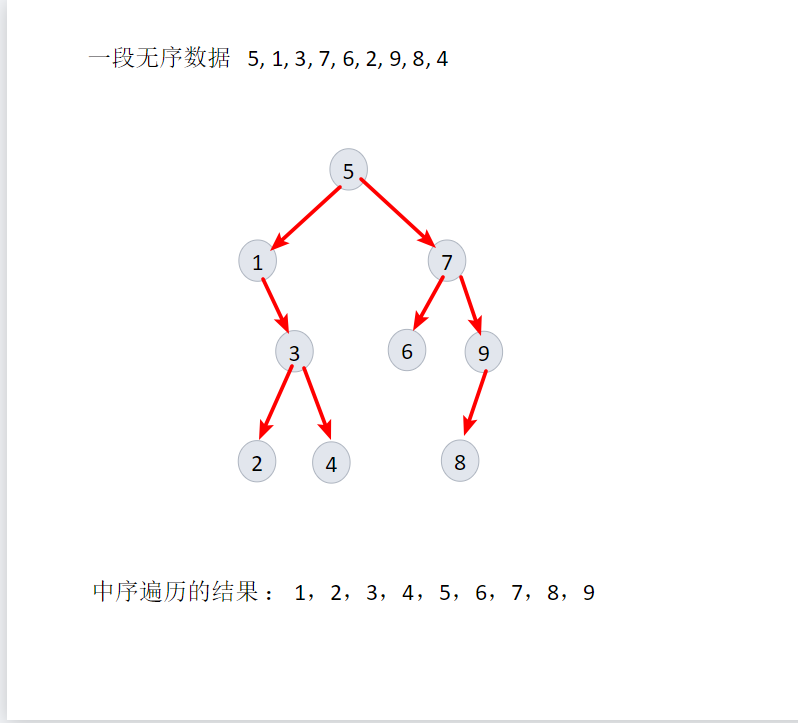
2、删除一个节点

　　删除的节点可以分为两种情况

　　1、可以直接删除的节点　　　　(左右子树不同时存在，或者左右子树为空)

　　2、需要替换删除的节点　　　　(左右子树同时存在)

补充：替换删除的时候，如何知道被删除节点需要被哪一个节点替换？

　　其实只要挑一个节点，让树的结构保持满足『左小右大』就行，可以是删除节点左子树里面的最大值，也可以是删除节点右子树里面的最大值(这里的代码实现使用了后者)

三、实现代码

　　1、类的构成

 1 class BiSortTree
 2 {
 3 public:
 4     BiSortTree();
 5     BiSortTree(int a[], int len);
 6     ~BiSortTree();
 7 
 8     pNode InsertBST(pNode root, int data);
 9     //这个安排也是秒得很，既可以实现无参打印整棵树，也有有参的可以选择
10     void middle_print() { middle_print(root); }
11     pNode SerchBST(int des) { return SerchBST(root, des); }
12     int DeleteBST(int des);
13 
14 private:
15     //可以指定根节点进行中序遍历
16     void middle_print(pNode root); //这个重载的设为private，不想被别人用
17     pNode SerchBST(pNode root, int des);
18     pNode DeleteBST(pNode p, pNode &root);
19     pNode successor(pNode root);
20     pNode root;
21 };

　　2、插入

 1 BiSortTree::BiSortTree(int a[], int len)
 2 {
 3     root = NULL;
 4     for (int i = 0; i < len; i++)
 5         root = InsertBST(root, a[i]);
 6     root->parent = NULL;
 7 }
 8 BiSortTree::~BiSortTree() {}
 9 
10 //插入算法，并且返回新增节点的指针
11 pNode BiSortTree::InsertBST(pNode root, int data)
12 {
13 
14     if (root == NULL)
15     {
16         pNode tmp = new Node;
17         tmp->data = data;
18         tmp->left = NULL;
19         tmp->right = NULL;
20         tmp->parent = NULL;
21         root = tmp;
22         return root;
23     }
24 
25     else if (data <= root->data)
26     {
27         root->left = InsertBST(root->left, data); //返回一个节点指针，实际上完成了叶节点的拓展
28         root->left->parent = root;
29     }
30     else
31     {
32         root->right = InsertBST(root->right, data);
33         root->right->parent = root;
34     }
35     return root; //做一个好的收尾
36 }

　　3、中序遍历

 1 //中序遍历算法，要求输入一个根节点 pNode root
 2 void BiSortTree::middle_print(pNode root)
 3 {
 4     if (root == NULL)
 5         return;
 6     else
 7     {
 8         middle_print(root->left);   //前序递归遍历root左子树
 9         printf("%d  ", root->data); //访问root的data
10         if (root->parent != NULL)
11             printf("    parent : %d\n", root->parent->data);
12         else
13             printf("    根节点\n");
14         middle_print(root->right); //
15     }
16 }

　　3、查找

 1 //查找算法，妙处就在于『递归』，太强大了
 2 pNode BiSortTree::SerchBST(pNode root, int des)
 3 {
 4     // if (root == NULL)
 5     //     return NULL;
 6     // else if (root->data == des)
 7     //     return root;
 8 
 9     if (root == NULL || root->data == des)
10         return root; //原来上面两句代码还可以1简洁到合在一起。厉害厉害。
11     else if (des <= root->data)
12         return SerchBST(root->left, des);
13     else
14         return SerchBST(root->right, des);
15 }

　　4、删除

 1 //查找右子树的最小节点，返回最小节点的指针
 2 pNode BiSortTree::successor(pNode root)
 3 {
 4     pNode p = root, s = root->right;
 5     if (s->left == NULL)
 6         return s;
 7     while (s->left != NULL)
 8     {
 9         p = s;
10         s = s->left;
11     }
12     return s;
13 }
14 
15 int BiSortTree::DeleteBST(int des)
16 {
17     pNode p = NULL;   //记录查找到的要被删除的节点
18     pNode del = NULL; //记录真正要被删除的节点      (注意这两个不一定一样的哦)
19     int result;
20     if ((p = SerchBST(des)) != NULL)
21     {
22         result = p->data;
23         if ((del = DeleteBST(p, root)) != NULL)
24             delete del;
25     }
26 
27     return result;
28 }
29 
30 pNode BiSortTree::DeleteBST(pNode p, pNode &root)
31 {
32     //补充一下，这里传一个引用很重要，因为有可能根节点的指向需要改变
33 
34     pNode y = NULL; //y用来指向代替p的节点
35     pNode x = NULL; //x用来指向y，以后的节点
36 
37     if ((p->left == NULL) || (p->right == NULL))
38     {
39         y = p;
40         printf("可以直接删除 %d\n", y->data);
41     }
42     else
43     {
44         y = successor(p);
45         printf("代替 %d 的将会是：%d\n", p->data, y->data);
46     }
47 
48     //确认x
49     if (y->left != NULL)
50         x = y->left;
51     else
52         x = y->right;
53 
54     if (x != NULL)
55         x->parent = y->parent; //将x回归大部队，因为下一步要把y分离出去了
56 
57     //把y分离出去
58     if (y->parent == NULL) //这样一个特殊情况(直接删除根节点)也考虑了，真的是太周到了
59         root = x;
60     else if (y == y->parent->left)
61         y->parent->left = x;
62     else
63         y->parent->right = x;
64 
65     //删除p,实际上只是删除了p的data，拿y作p的替代
66     if (y != p)
67         p->data = y->data;
68 
69     return y;
70 }

　　5、main测试

 1 int main(void)
 2 {
 3     int a[] = {5, 1, 3, 7, 6, 2, 9, 8, 4};
 4     int len = 9;
 5     int val = 7;
 6     BiSortTree bt(a, len);
 7     bt.middle_print();
 8 
 9     for (int i = 1; i <= 9; i++)
10     {
11         if (bt.SerchBST(i))
12             printf("查找成功 %d\n", bt.SerchBST(i)->data);
13 
14         else
15             printf("查找失败 %d\n", i);
16     }
17 
18     for (int i = 1; i <= 9; i++)
19     {
20         printf("删除了  %d\n", bt.DeleteBST(i));
21     }
22 
23     bt.middle_print();
24     return 0;
25 }

　　6、输出

 1 /* 
 2 ——————————————————————————————————
 3 1      parent : 5
 4 2      parent : 3
 5 3      parent : 1
 6 4      parent : 3
 7 5      根节点    
 8 6      parent : 7
 9 7      parent : 5
10 8      parent : 9
11 9      parent : 7
12 查找成功 1
13 查找成功 2
14 查找成功 3
15 查找成功 4
16 查找成功 5
17 查找成功 6
18 查找成功 7
19 查找成功 8
20 查找成功 9
21 可以直接删除 1
22 删除了  1
23 可以直接删除 2
24 删除了  2
25 可以直接删除 3
26 删除了  3
27 可以直接删除 4
28 删除了  4
29 可以直接删除 5
30 删除了  5
31 可以直接删除 6
32 删除了  6
33 可以直接删除 7
34 删除了  7
35 可以直接删除 8
36 删除了  8
37 可以直接删除 9
38 删除了  9
39 ——————————————————————————————————
40  */

　　7、全部代码

  1 /*
  2  created by coderon
  3     26 August 2020
  4 */
  5 #include <stdio.h>
  6 
  7 typedef struct NODE
  8 {
  9     int data;
 10     NODE *left;
 11     NODE *right;
 12     NODE *parent;
 13 } Node, *pNode;
 14 
 15 class BiSortTree
 16 {
 17 public:
 18     BiSortTree();
 19     BiSortTree(int a[], int len);
 20     ~BiSortTree();
 21 
 22     pNode InsertBST(pNode root, int data);
 23     //这个安排也是秒得很，既可以实现无参打印整棵树，也有有参的可以选择
 24     void middle_print() { middle_print(root); }
 25     pNode SerchBST(int des) { return SerchBST(root, des); }
 26     int DeleteBST(int des);
 27 
 28 private:
 29     //可以指定根节点进行中序遍历
 30     void middle_print(pNode root); //这个重载的设为private，不想被别人用
 31     pNode SerchBST(pNode root, int des);
 32     pNode DeleteBST(pNode p, pNode &root);
 33     pNode successor(pNode root);
 34     pNode root;
 35 };
 36 
 37 BiSortTree::BiSortTree(int a[], int len)
 38 {
 39     root = NULL;
 40     for (int i = 0; i < len; i++)
 41         root = InsertBST(root, a[i]);
 42     root->parent = NULL;
 43 }
 44 BiSortTree::~BiSortTree() {}
 45 
 46 //插入算法，并且返回新增节点的指针
 47 pNode BiSortTree::InsertBST(pNode root, int data)
 48 {
 49 
 50     if (root == NULL)
 51     {
 52         pNode tmp = new Node;
 53         tmp->data = data;
 54         tmp->left = NULL;
 55         tmp->right = NULL;
 56         tmp->parent = NULL;
 57         root = tmp;
 58         return root;
 59     }
 60 
 61     else if (data <= root->data)
 62     {
 63         root->left = InsertBST(root->left, data); //返回一个节点指针，实际上完成了叶节点的拓展
 64         root->left->parent = root;
 65     }
 66     else
 67     {
 68         root->right = InsertBST(root->right, data);
 69         root->right->parent = root;
 70     }
 71     return root; //做一个好的收尾
 72 }
 73 
 74 //中序遍历算法，要求输入一个根节点 pNode root
 75 void BiSortTree::middle_print(pNode root)
 76 {
 77     if (root == NULL)
 78         return;
 79     else
 80     {
 81         middle_print(root->left);   //前序递归遍历root左子树
 82         printf("%d  ", root->data); //访问root的data
 83         if (root->parent != NULL)
 84             printf("    parent : %d\n", root->parent->data);
 85         else
 86             printf("    根节点\n");
 87         middle_print(root->right); //
 88     }
 89 }
 90 
 91 //查找算法，妙处就在于『递归』，太强大了
 92 pNode BiSortTree::SerchBST(pNode root, int des)
 93 {
 94     // if (root == NULL)
 95     //     return NULL;
 96     // else if (root->data == des)
 97     //     return root;
 98 
 99     if (root == NULL || root->data == des)
100         return root; //原来上面两句代码还可以1简洁到合在一起。厉害厉害。
101     else if (des <= root->data)
102         return SerchBST(root->left, des);
103     else
104         return SerchBST(root->right, des);
105 }
106 
107 //查找右子树的最小节点，返回最小节点的指针
108 pNode BiSortTree::successor(pNode root)
109 {
110     pNode p = root, s = root->right;
111     if (s->left == NULL)
112         return s;
113     while (s->left != NULL)
114     {
115         p = s;
116         s = s->left;
117     }
118     return s;
119 }
120 
121 int BiSortTree::DeleteBST(int des)
122 {
123     pNode p = NULL;   //记录查找到的要被删除的节点
124     pNode del = NULL; //记录真正要被删除的节点      (注意这两个不一定一样的哦)
125     int result;
126     if ((p = SerchBST(des)) != NULL)
127     {
128         result = p->data;
129         if ((del = DeleteBST(p, root)) != NULL)
130             delete del;
131     }
132 
133     return result;
134 }
135 
136 pNode BiSortTree::DeleteBST(pNode p, pNode &root)
137 {
138     //补充一下，这里传一个引用很重要，因为有可能根节点的指向需要改变
139 
140     pNode y = NULL; //y用来指向代替p的节点
141     pNode x = NULL; //x用来指向y，以后的节点
142 
143     if ((p->left == NULL) || (p->right == NULL))
144     {
145         y = p;
146         printf("可以直接删除 %d\n", y->data);
147     }
148     else
149     {
150         y = successor(p);
151         printf("代替 %d 的将会是：%d\n", p->data, y->data);
152     }
153 
154     //确认x
155     if (y->left != NULL)
156         x = y->left;
157     else
158         x = y->right;
159 
160     if (x != NULL)
161         x->parent = y->parent; //将x回归大部队，因为下一步要把y分离出去了
162 
163     //把y分离出去
164     if (y->parent == NULL) //这样一个特殊情况(直接删除根节点)也考虑了，真的是太周到了
165         root = x;
166     else if (y == y->parent->left)
167         y->parent->left = x;
168     else
169         y->parent->right = x;
170 
171     //删除p,实际上只是删除了p的data，拿y作p的替代
172     if (y != p)
173         p->data = y->data;
174 
175     return y;
176 }
177 
178 int main(void)
179 {
180     int a[] = {5, 1, 3, 7, 6, 2, 9, 8, 4};
181     int len = 9;
182     int val = 7;
183     BiSortTree bt(a, len);
184     bt.middle_print();
185 
186     for (int i = 1; i <= 9; i++)
187     {
188         if (bt.SerchBST(i))
189             printf("查找成功 %d\n", bt.SerchBST(i)->data);
190 
191         else
192             printf("查找失败 %d\n", i);
193     }
194 
195     for (int i = 1; i <= 9; i++)
196     {
197         printf("删除了  %d\n", bt.DeleteBST(i));
198     }
199 
200     bt.middle_print();
201     return 0;
202 }
203 /* 
204 ——————————————————————————————————
205 1      parent : 5
206 2      parent : 3
207 3      parent : 1
208 4      parent : 3
209 5      根节点    
210 6      parent : 7
211 7      parent : 5
212 8      parent : 9
213 9      parent : 7
214 查找成功 1
215 查找成功 2
216 查找成功 3
217 查找成功 4
218 查找成功 5
219 查找成功 6
220 查找成功 7
221 查找成功 8
222 查找成功 9
223 可以直接删除 1
224 删除了  1
225 可以直接删除 2
226 删除了  2
227 可以直接删除 3
228 删除了  3
229 可以直接删除 4
230 删除了  4
231 可以直接删除 5
232 删除了  5
233 可以直接删除 6
234 删除了  6
235 可以直接删除 7
236 删除了  7
237 可以直接删除 8
238 删除了  8
239 可以直接删除 9
240 删除了  9
241 ——————————————————————————————————
242  */

全部代码

总结：

　　程序不可能一下子就无懈可击，总是有想得不周到的地方，这时候需要的是冷静有逻辑的判断，有时候机械地一句一句地执行也会发现许多意想不到的收获。

posted on 2020-08-26 00:43 Coderon 阅读(210) 评论(0) 编辑收藏举报

刷新页面返回顶部

查找：二叉查找树 c++ 2020年8月

一、实现思想

二、实现图例

三、实现代码

1、类的构成

2、插入

3、中序遍历

3、查找

4、删除

5、main测试

6、输出

7、全部代码

总结：

公告

　　1、类的构成

　　2、插入

　　3、中序遍历

　　3、查找

　　4、删除

　　5、main测试

　　6、输出

　　7、全部代码