一、实现思想
这里以数组作为存储结构，用假设出来的堆作为实现基础
1、将最大值调整到堆顶
2、将堆顶摘除，移动到数组末尾
3、将剩下元素，重新构建堆，堆顶又是最大值，又移动到后面
4、重复以上步骤，直到数组剩下最后一个元素
注意：最核心的步骤就在于堆的构建与调整(也是比较难讲述清楚的部分)
二、图例实现
1
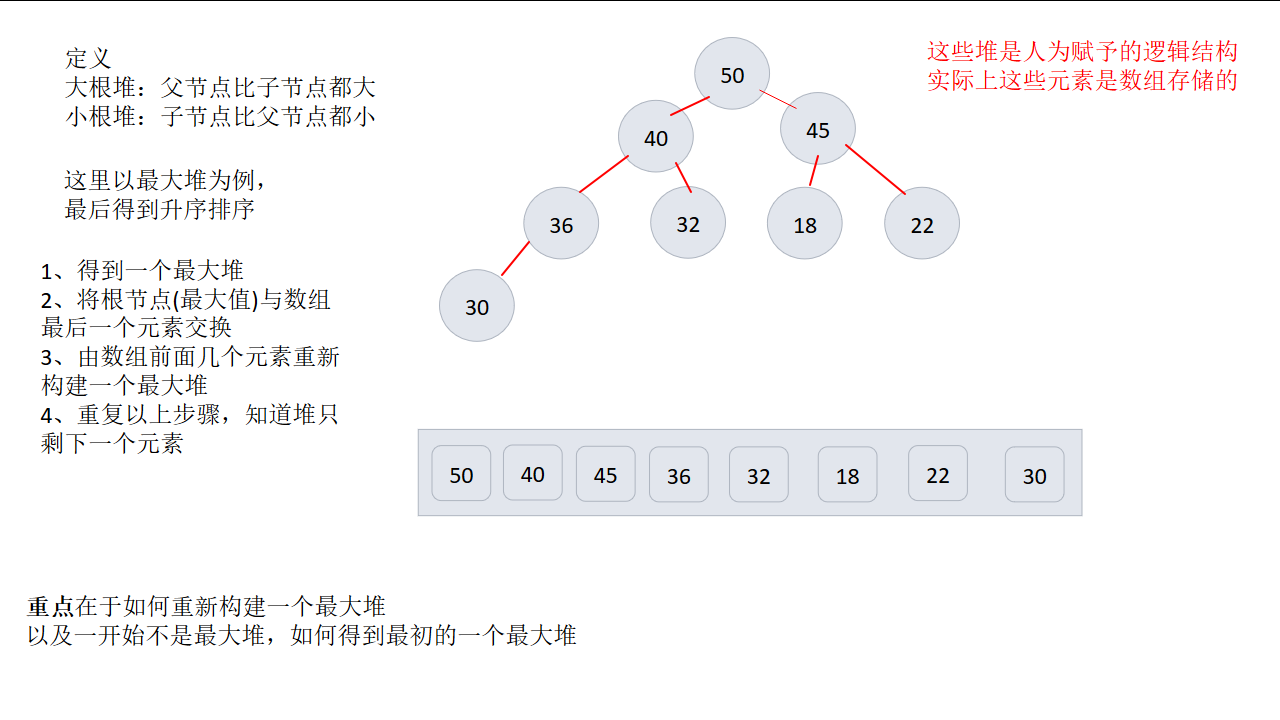
2、
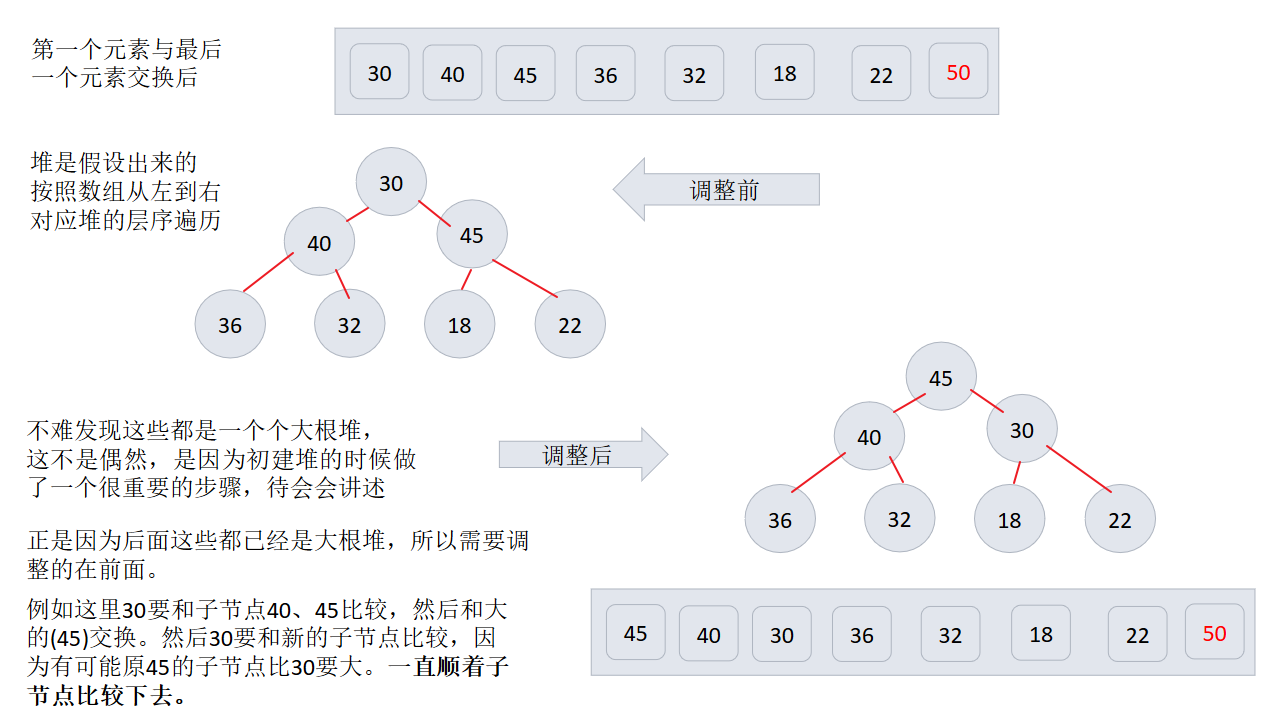
3、
4、
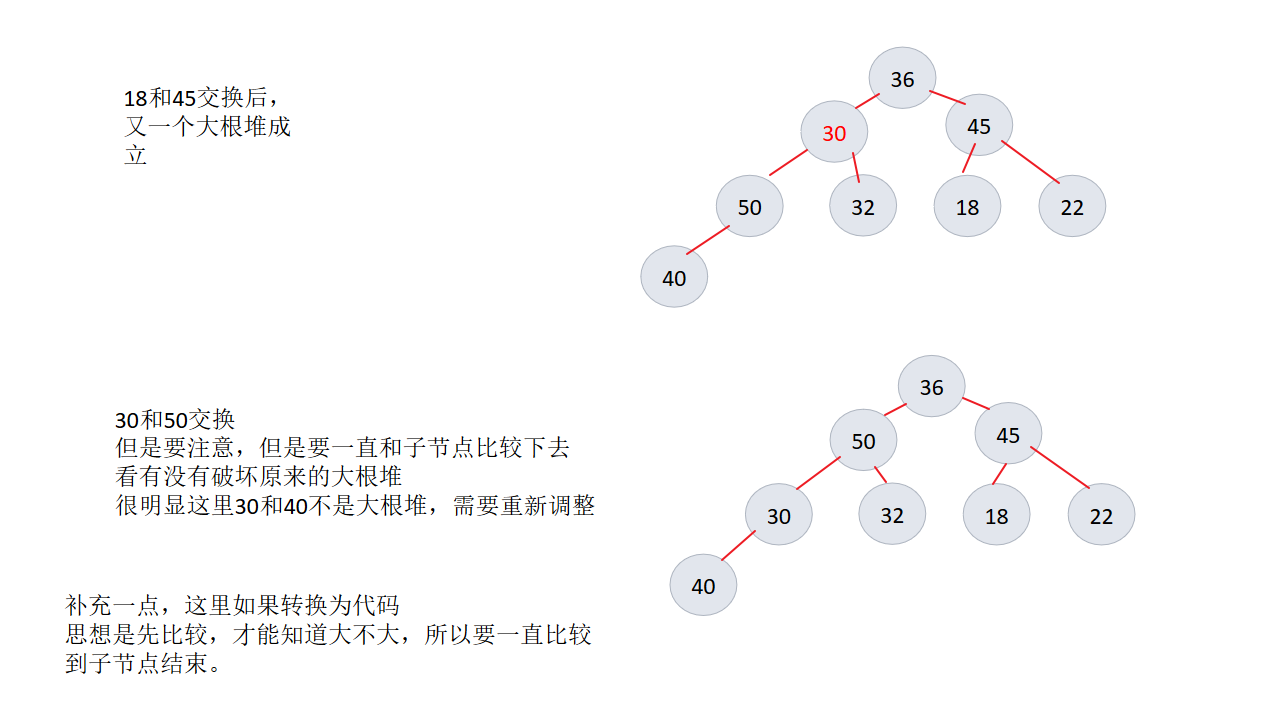
5、
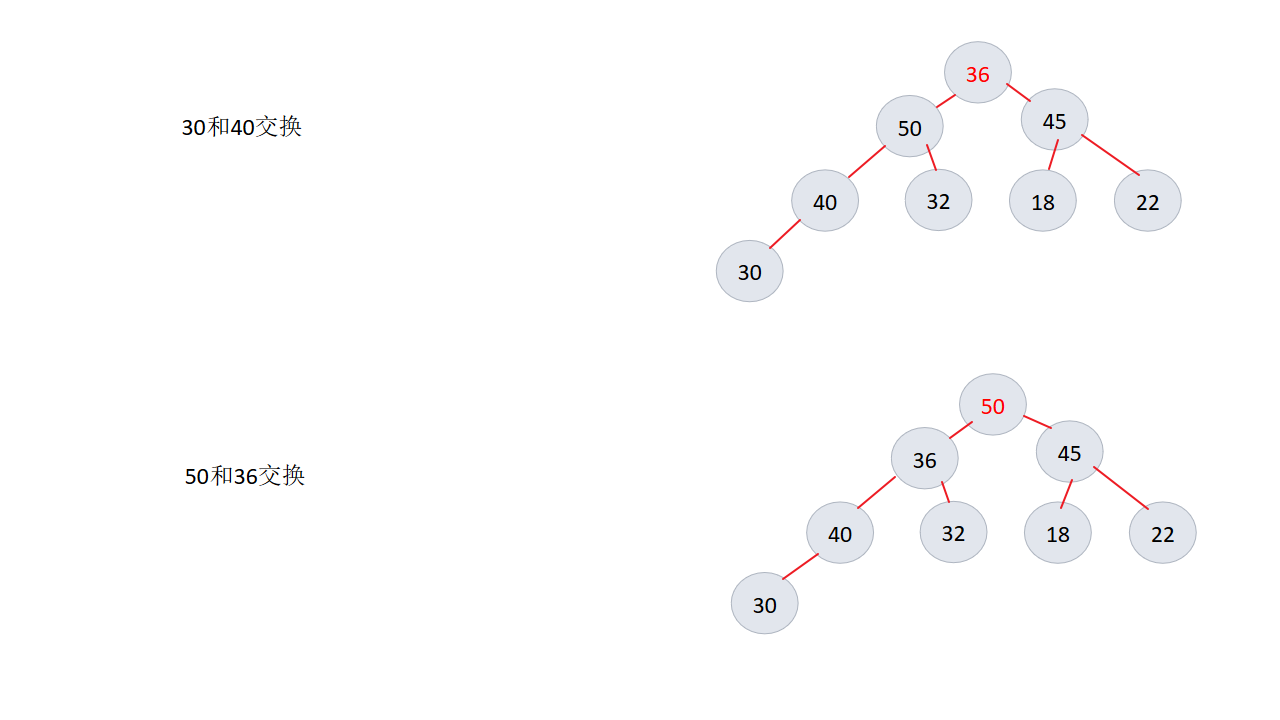
6、
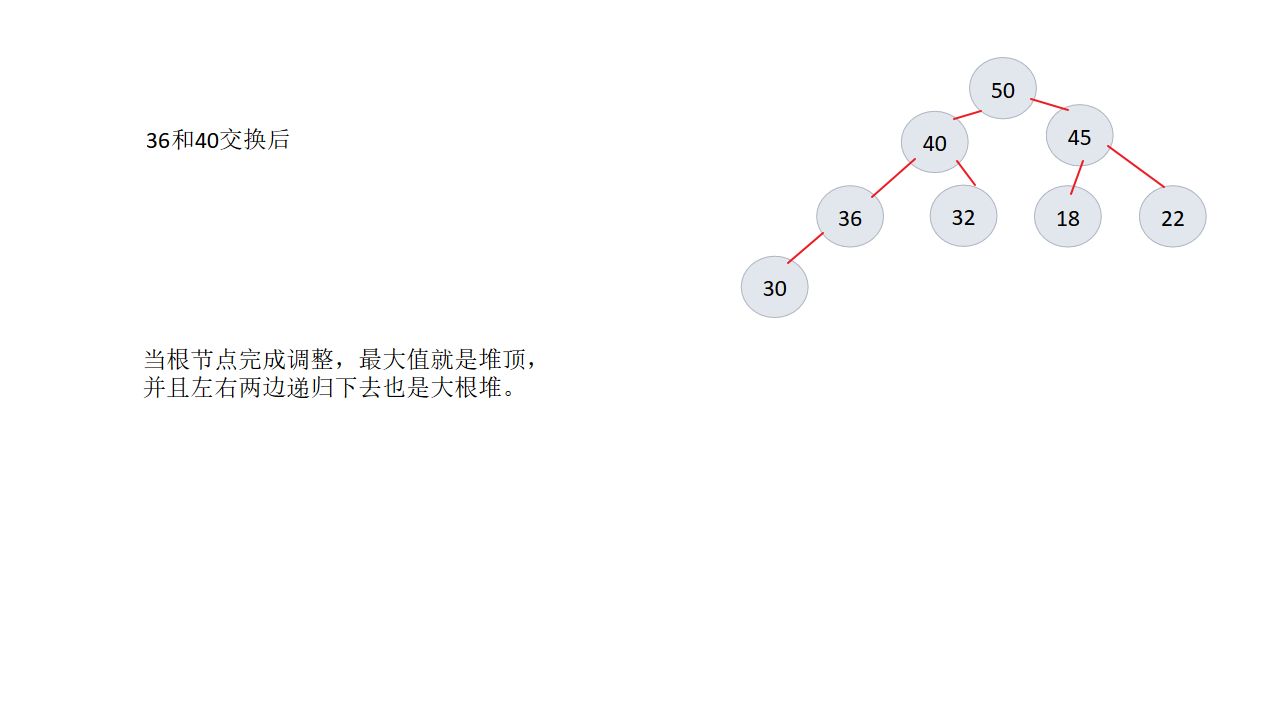
三、实现代码
有很多小细节要注意，很难一一说清楚，但是意会理解起来比较容易，可以按照下面框架去理解。
1、输入一个k为顶的位置，调整k为顶的堆为大根堆的一个函数，sifi函数
2、通过循环调用sifi函数，实现初建堆，
1 for (i = len / 2 - 1; i >= 0; i--) //当然这里的i可以改成len ,但是后面几个都是在做无用功，没必要，这也是一个妙处 2 //从最后一个分支节点调整至根节点，实现新建堆(最大堆或最小堆)，当然我这里只是实现了最大堆 3 sift(i, len - 1);
3、接下来是移动堆顶到后面，并且重新调整堆，使堆顶是下一个最大值
1 for (i = 1; i < len; i++) 2 { 3 temp = data[0]; 4 data[0] = data[len - i]; 5 data[len - i] = temp; 6 sift(0, len - i - 1); 7 }
完整实现代码
1 #include <stdio.h> 2 int data[] = {36, 30, 18, 40, 32, 45, 22, 50}; 3 //对以k为顶的堆，进行调整为大根堆或者小根堆 4 /* 将完全二叉树存储到data[0]~data[length-1],则data[i]的左孩子是data[2*i+1] */ 5 void sift(int k, int last) 6 { 7 int i, j, temp; 8 i = k; 9 10 j = 2 * i + 1; //i是被调整节点，j是i的左孩子 11 while (j <= last) 12 { 13 if (j < last && data[j] < data[j + 1]) 14 j++; //j指向左右孩子的较大者//当然啦，如果想要变成最小堆，换一下符号即可 15 if (data[i] > data[j]) 16 break; //已经是堆，不用交换 17 else 18 { 19 temp = data[j]; 20 data[j] = data[i]; 21 data[i] = temp; 22 i = j; 23 j = 2 * i + 1; //开始往下走 24 } 25 } 26 } 27 28 void HeadSort(int len) 29 { 30 int i, temp; 31 for (i = len / 2 - 1; i >= 0; i--) //当然这里的i可以改成len ,但是后面几个都是在做无用功，没必要，这也是一个妙处 32 //从最后一个分支节点调整至根节点，实现新建堆(最大堆或最小堆)，当然我这里只是实现了最大堆 33 sift(i, len - 1); 34 for (i = 1; i < len; i++) 35 { 36 temp = data[0]; 37 data[0] = data[len - i]; 38 data[len - i] = temp; 39 sift(0, len - i - 1); 40 } 41 } 42 43 int main(void) 44 { 45 int len = 8; 46 for (int i = 0; i < len; i++) 47 printf("%d ", data[i]); 48 printf("\n"); 49 HeadSort(len); 50 for (int i = 0; i < len; i++) 51 printf("%d ", data[i]); 52 return 0; 53 } 54 /* 55 输出 56 ———————————————————————————————————————————— 57 36 30 18 40 32 45 22 50 58 18 22 30 32 36 40 45 50 59 ———————————————————————————————————————————— 60 */
(ps:我这里显示了行号，复制也会一同复制过去。你应该会竖直选择然后删除吧)
