L1-7蛇皮走位，原题《CCF201412-2 Z字形扫描》

L1-7蛇皮走位，原题《CCF201412-2 Z字形扫描》

在图像编码的算法中，需要将一个给定的方形矩阵进行Z字形扫描(Zigzag Scan)。给定一个n×n的矩阵，Z字形扫描的过程如下图所示：

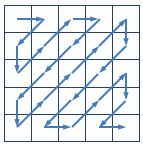
　　请实现一个Z字形扫描的程序，给定一个n×n的矩阵，输出对这个矩阵进行Z字形扫描的结果。

评测用例规模与约定

1≤n≤500，矩阵元素为不超过1000的正整数。

输入格式:

输入的第一行包含一个整数n，表示矩阵的大小。输入的第二行到第n+1行每行包含n个正整数，由空格分隔，表示给定的矩阵。

输出格式:

输出一行，包含n×n个整数，由空格分隔，表示输入的矩阵经过Z字形扫描后的结果。

输入样例:

在这里给出一组输入。例如：

4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

输出样例:

在这里给出相应的输出。例如：

1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3

想法

如果叫我们依次输出一个数组的每一行每个元素，我们肯定能闭着眼睛就能写一个双重循环！
但是问题中给的是Z字形遍历，这该怎么直来直去地遍历呢？

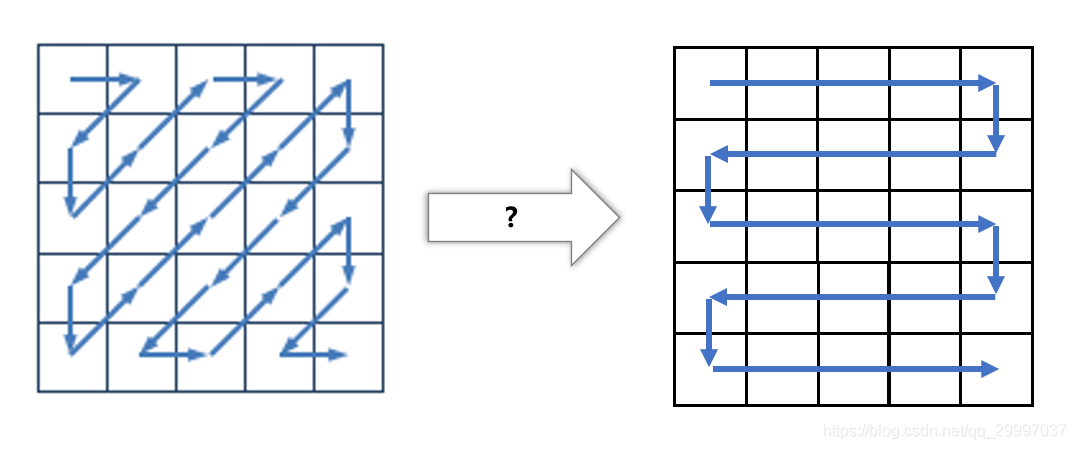
如果我们换个方向，将左图旋转45°，就可以直来直去地进行遍历了！我们将遍历层数变成了0层-8层共九层，每一层的个数不相同。也就是说，转换成 vector<vector<int>> vec(2*n + 1)，遍历的时候只是把每一层的个数取 vec[i].size() 即可。其中 2*n+1 是有规律可循的：

当n = 1时，level = 1
当n = 2时，level = 3
当n = 3时，level = 5
…
当n = k时，level = 2 * k + 1

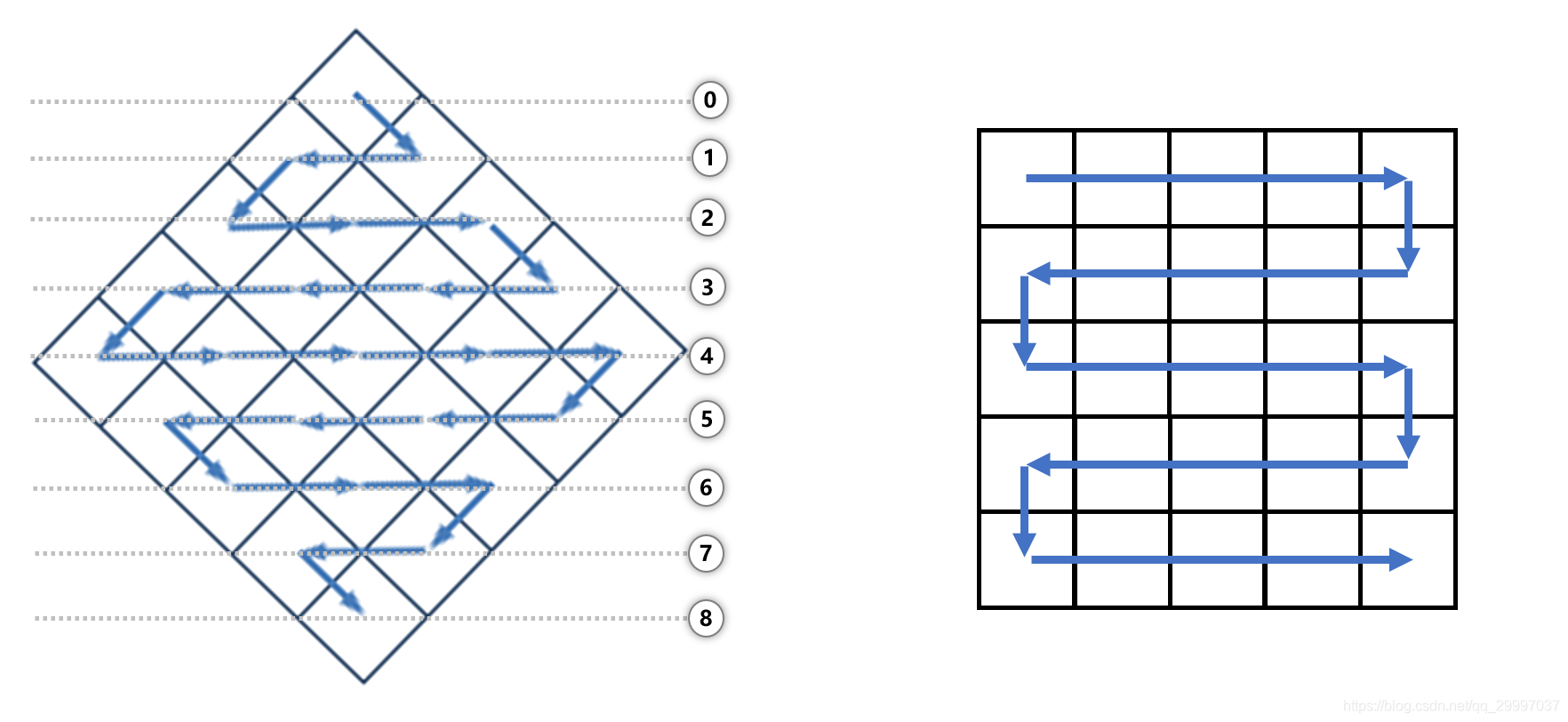
接下来如果换方向呢？
可以观察到，当小球遍历的时候，层数其实就是当前元素在数组中的坐标之和 level = i + j

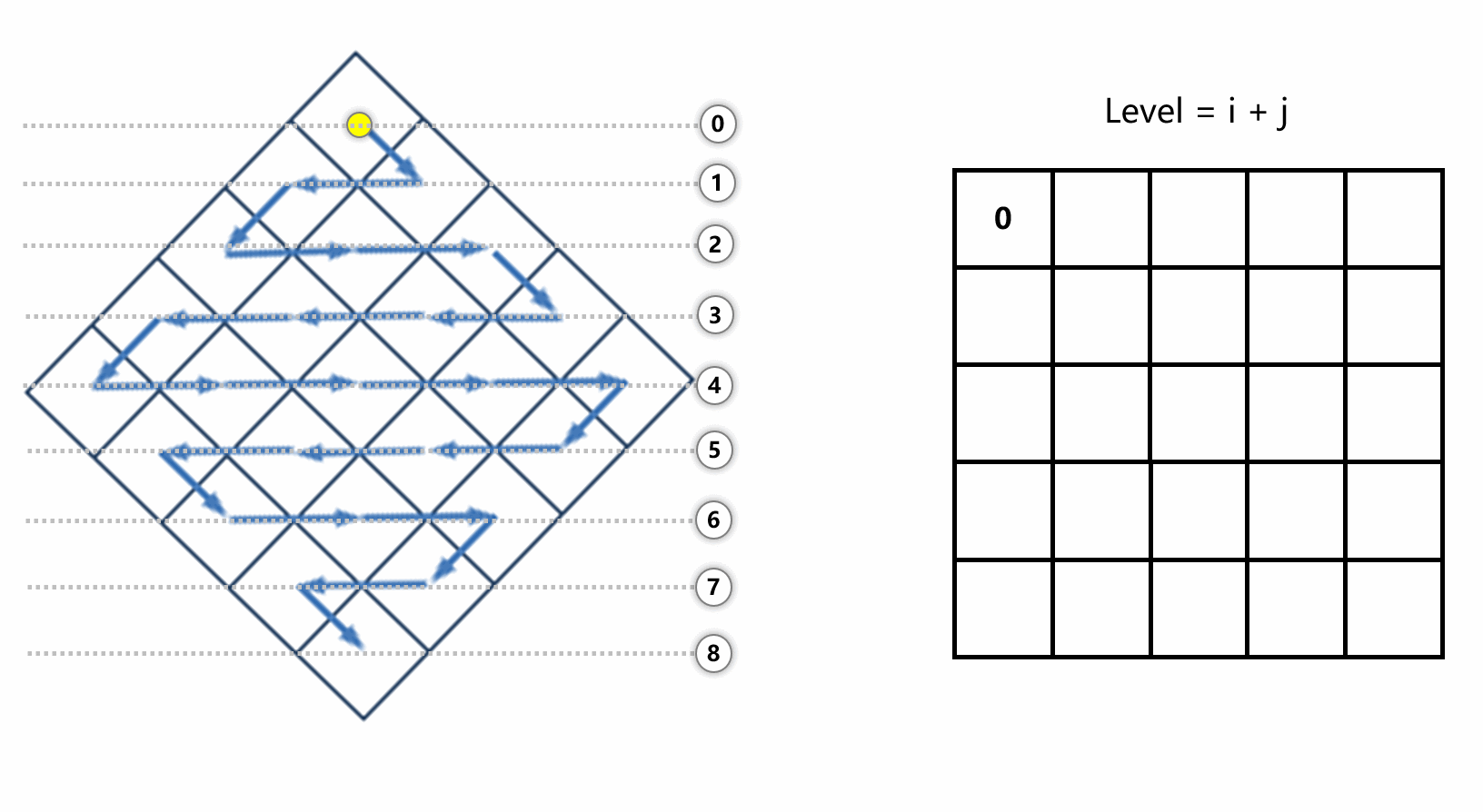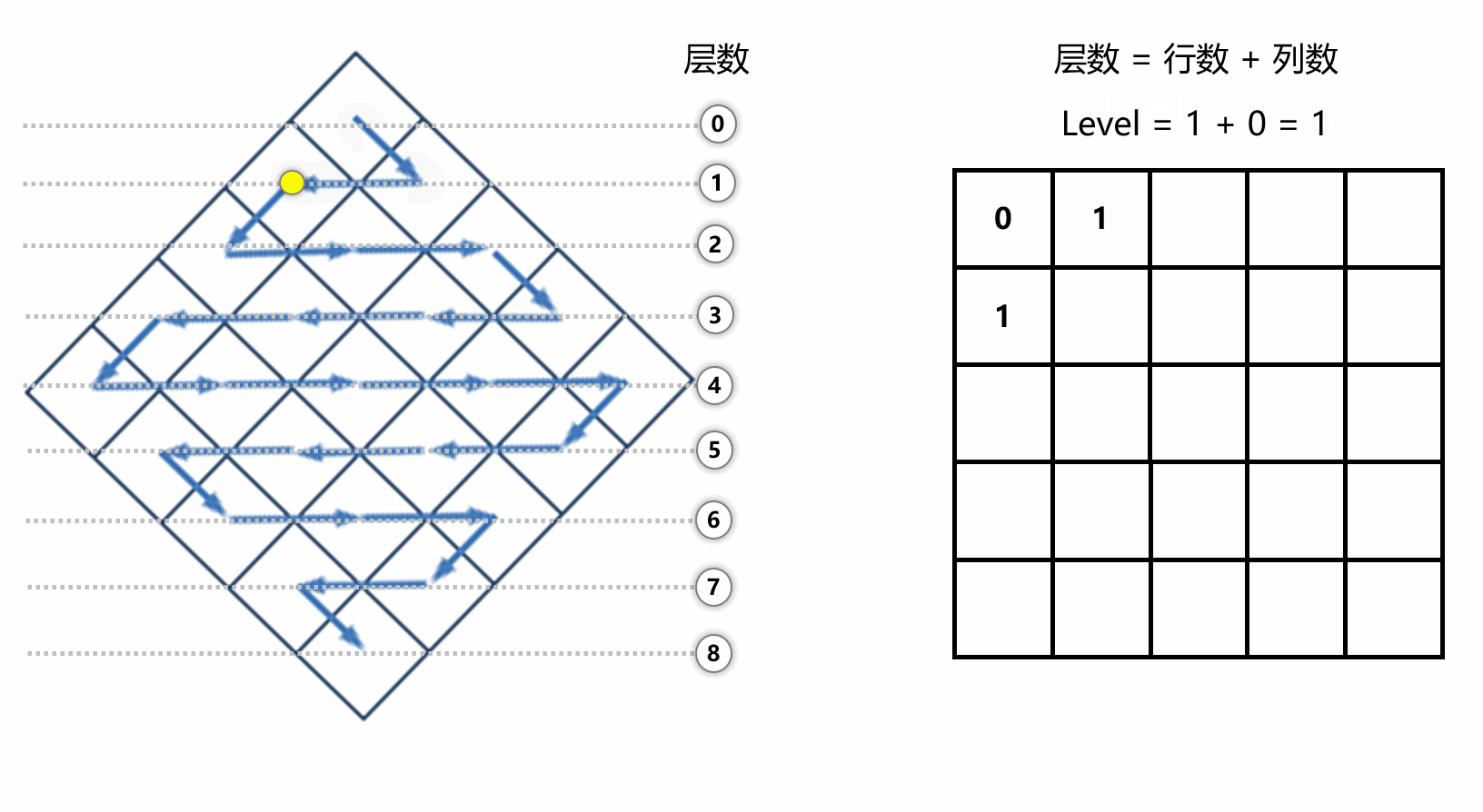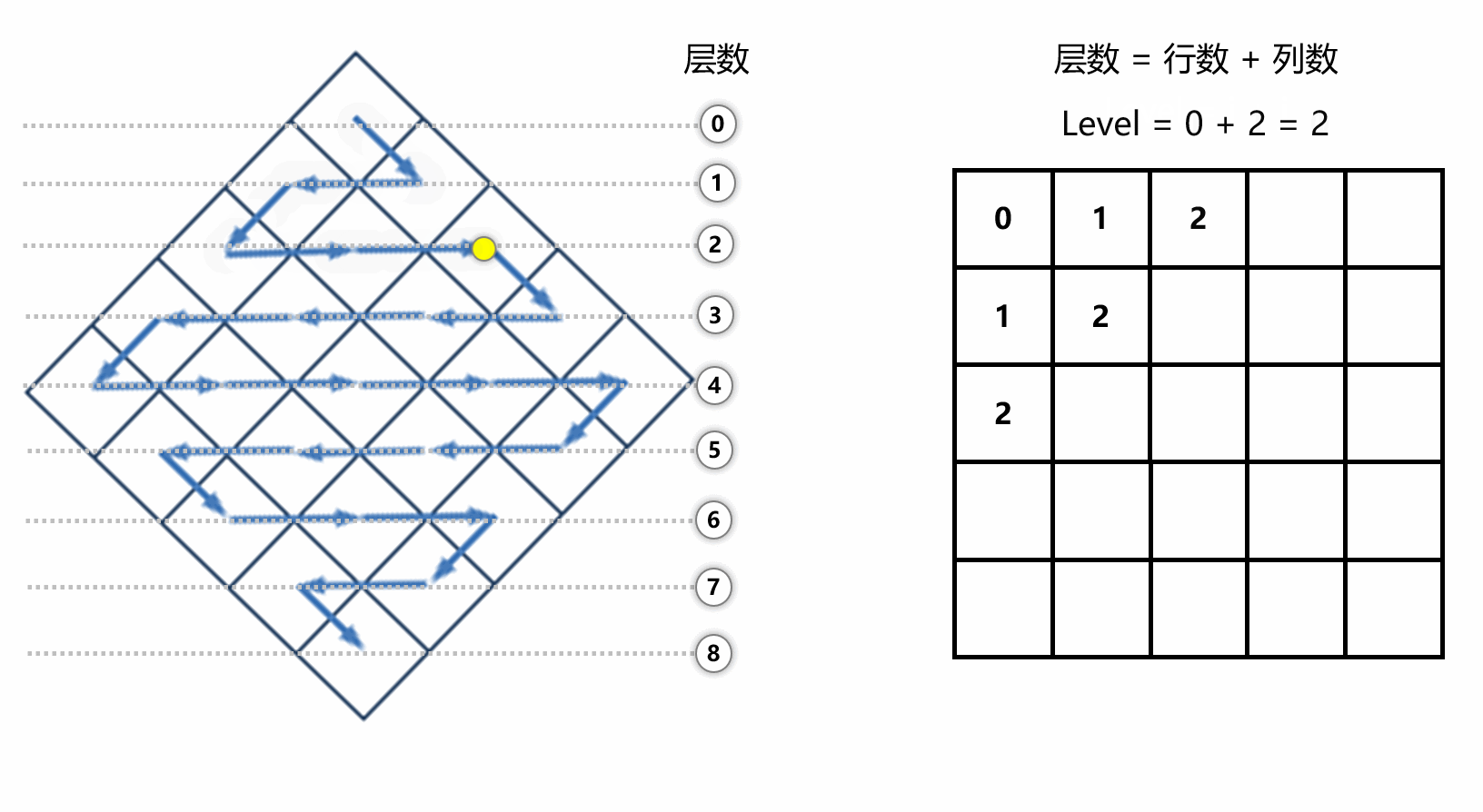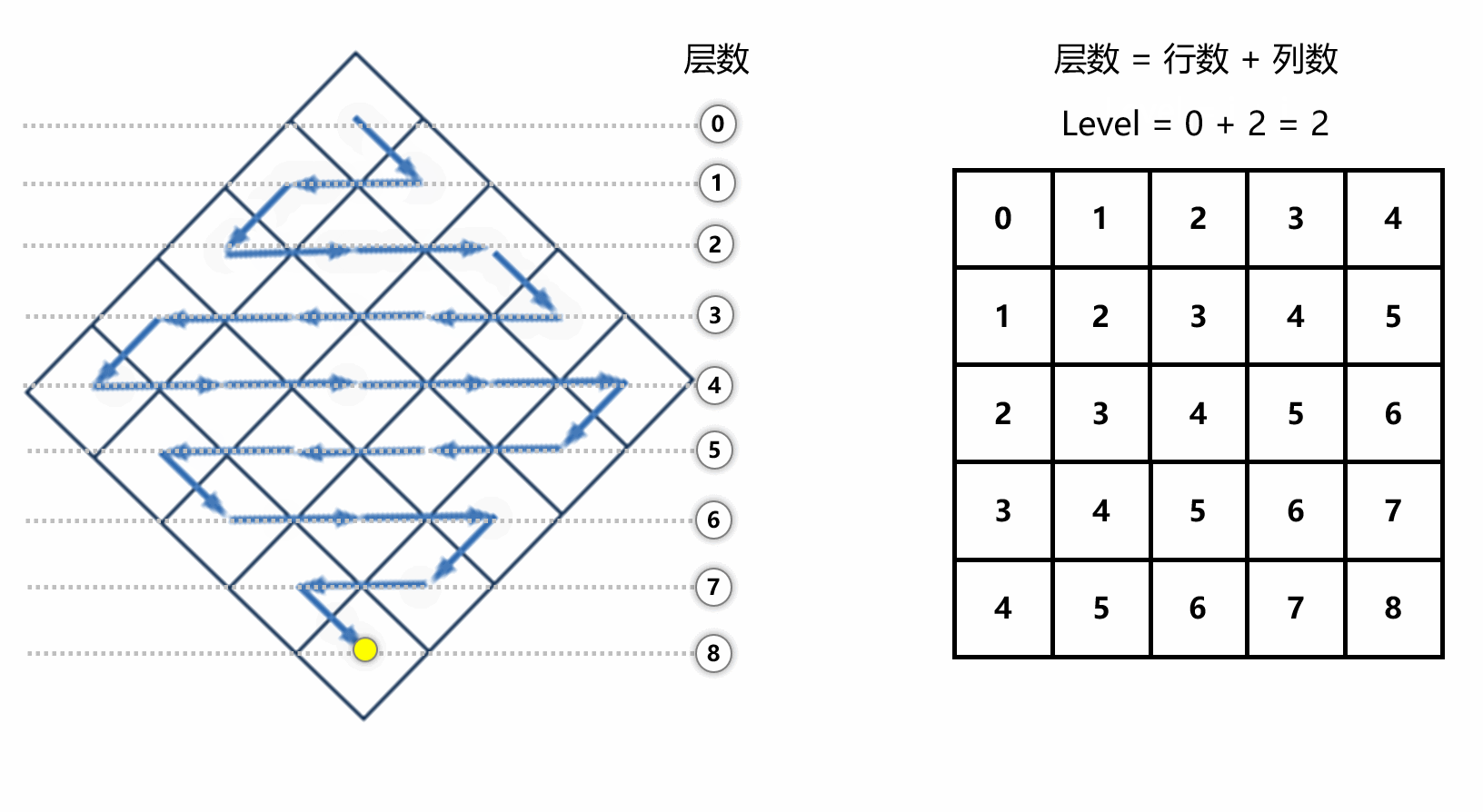
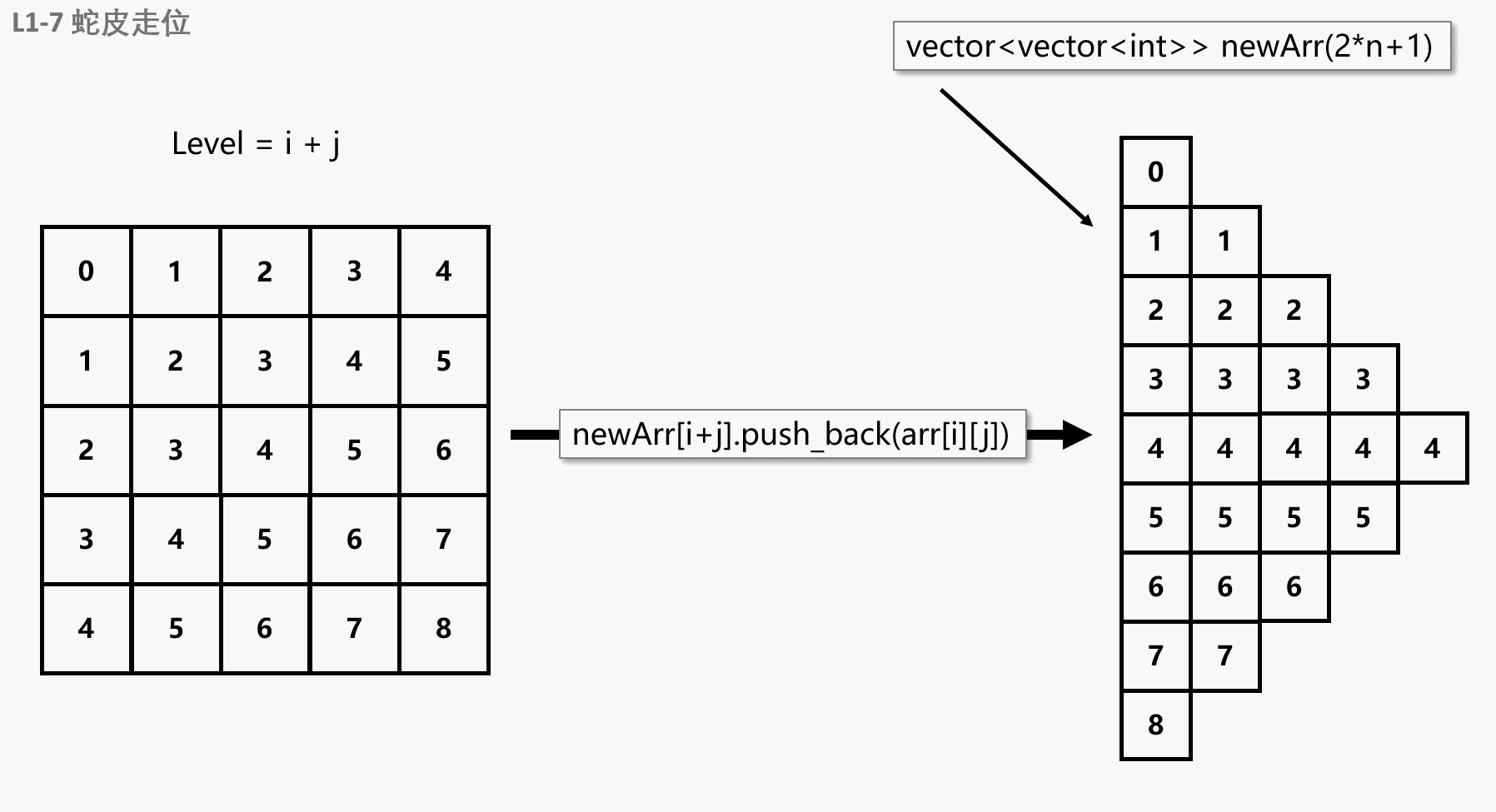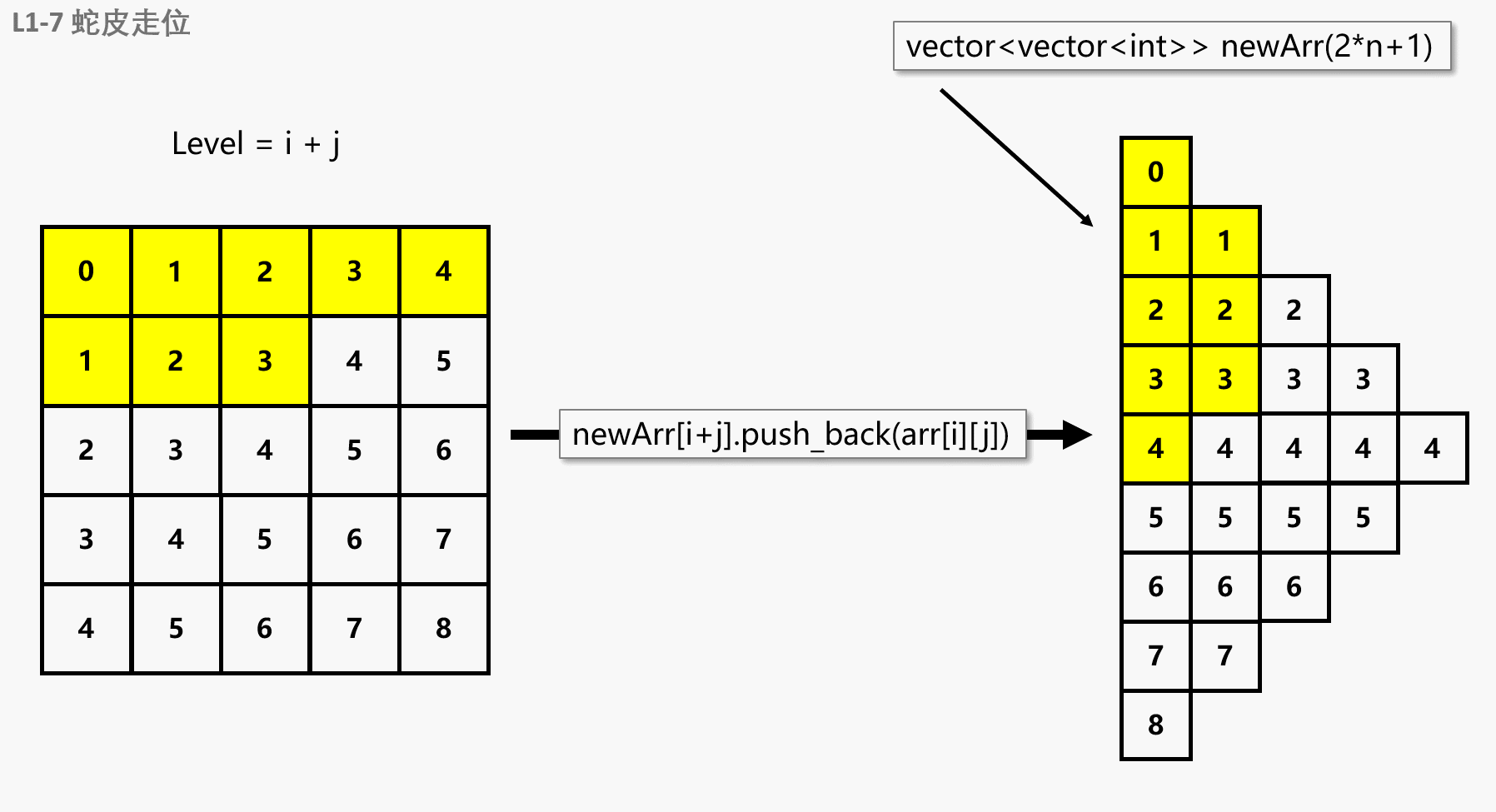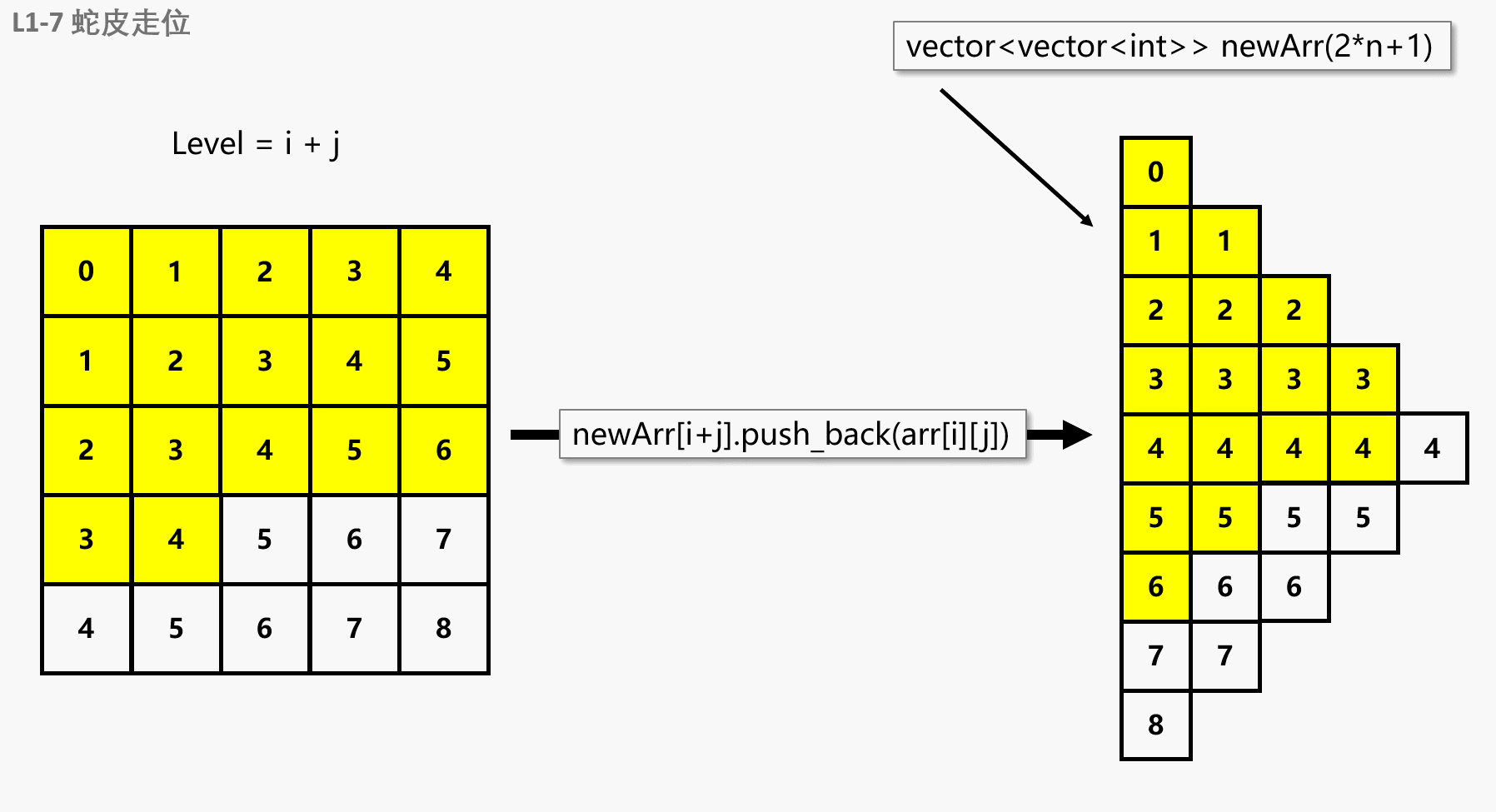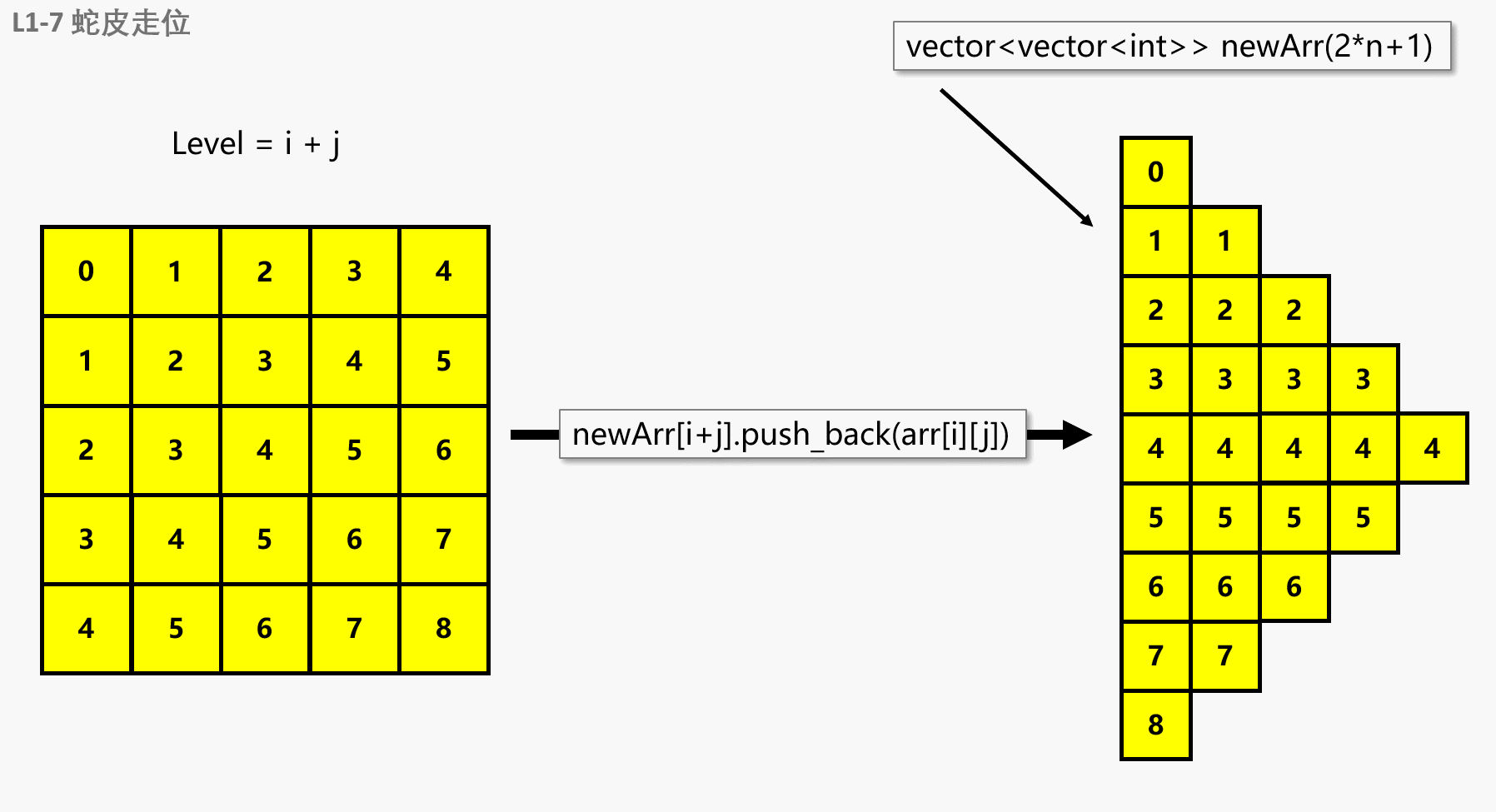
下面展示一下转换过程，其实就是每次遍历的时候，执行 newArr[i + j].push_back(arr[i][j]) 即可
因为访问新数组每一层的时候，都是前面的先被访问到，所以不用担心会出现乱序的情况。

参考代码

#include<iostream>
#include<vector>
using namespace std;

int main() {
    int n;  cin>>n;
    vector<vector<int>> vec(2*n-1);
    int num;
    for(int i=0;i<n;++i) {
        for(int j=0;j<n;++j) {
            cin>>num;
            vec[i + j].push_back(num);
        }
    }
    bool reOrder = true;   // 是否反序
    for(int i=0;i<vec.size();++i) {
        if(reOrder)
            reverse(vec[i].begin(), vec[i].end());
        for(int j=0;j<vec[i].size();++j)
            cout<<vec[i][j]<<(i==vec.size()-1 && j == vec[i].size() - 1?"":" ");
        reOrder = !reOrder;
    }
    return 0;
}