LeetCode 1339. Maximum Product of Splitted Binary Tree

Given a binary tree root. Split the binary tree into two subtrees by removing 1 edge such that the product of the sums of the subtrees are maximized.

Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

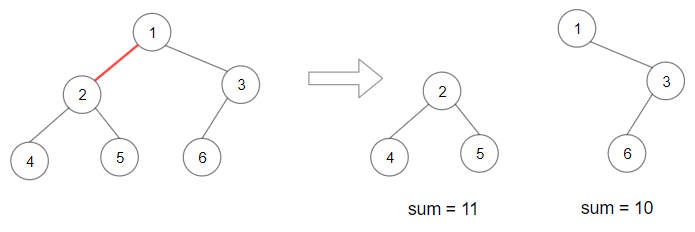
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

Example 2:

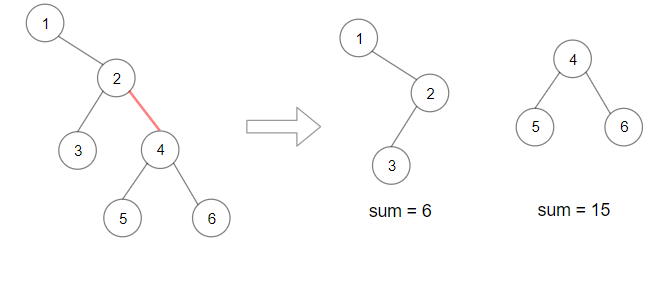
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation:  Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

Example 3:

Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025

Example 4:

Input: root = [1,1]
Output: 1

Constraints:

Each tree has at most 50000 nodes and at least 2 nodes.
Each node's value is between [1, 10000].

实现思路：

拆分二叉树，使得两棵树的结点权值和的乘积最大，回溯法。

AC代码：

class Solution {
		long long maxN=0;
		const long long N=1e9+7;
		unordered_map<TreeNode*,int> mp;
	public:
	//计算树的总的权值和
		void getALL(TreeNode *root,int &sum) {
			if(!root) return;
			sum+=(root->val);
			getALL(root->left,sum);
			getALL(root->right,sum);
		}
		//采用回溯法大大提升了效率
		int dfs(TreeNode *root,int all) {
			if(root==NULL) return 0;
			int l= dfs(root->left,all);
			int r=dfs(root->right,all);
			int key=l+r+root->val;
			if((long long)key*(all-key)>maxN) maxN=(long long)key*(all-key);
			return key;
		}

		int maxProduct(TreeNode* root) {
			int sum=0;
			getALL(root,sum);
			dfs(root,sum);
			return maxN%N;
		}
};

下面给出超时的写法

超时的写法
void dfs(TreeNode *root,int all) {
	if(root==NULL) return;
	dfs(root->left,all);
	dfs(root->right,all);
	int key=0;
	getALL(root,key);
	if((long long)key*(all-key)>maxN) maxN=(long long)key*(all-key);
}

采用上面这种方法的话，会每次递归都计算一次当前结点作为根结点的树的权值和，等于递归套递归大大增加了时间复杂度。