LeetCode 310. Minimum Height Trees

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

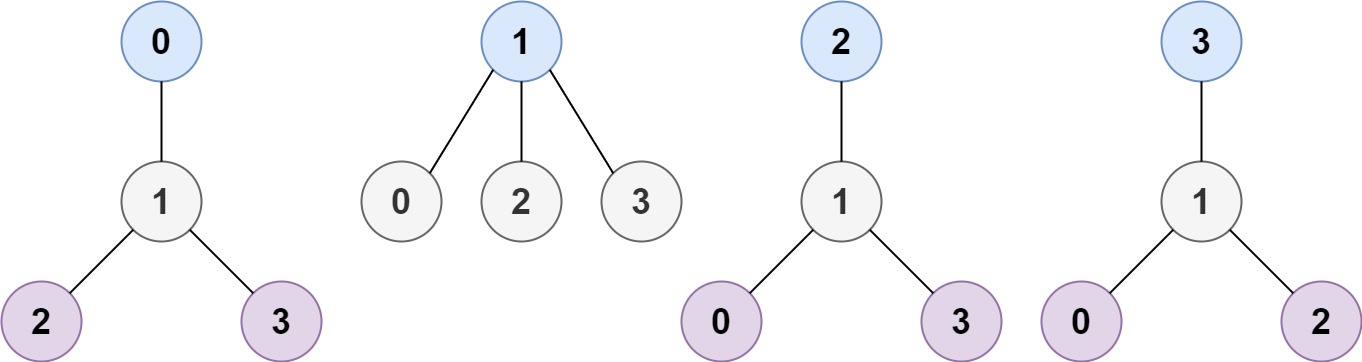
Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

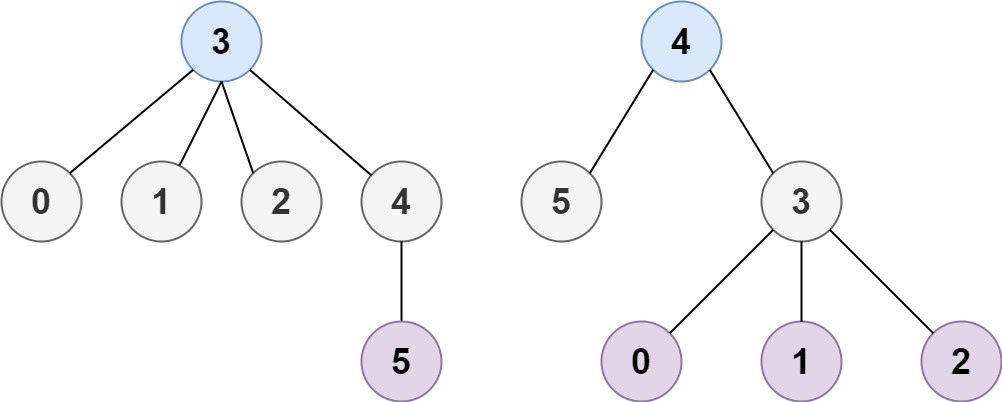
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Example 3:

Input: n = 1, edges = []
Output: [0]

Example 4:

Input: n = 2, edges = [[0,1]]
Output: [0,1]

Constraints:

1 <= n <= 2 * 104
edges.length == n - 1
0 <= ai, bi < n
ai != bi
All the pairs (ai, bi) are distinct.
The given input is guaranteed to be a tree and there will be no repeated edges.

实现思路：
有点类似拓扑，利用删去度为1的结点，这里把入度和出度算一者了，然后再一层层删去，队列加入度为1的结点，直到队列最后一层只有不多于2个结点的情况，就是能够组成最小高度的树的根节点。
这里的证明就是1 2 3 4 5连成一条线，若让树高度越小，结点只能越是中间的结点，当一条线是偶数结点则中间结点有2个。是奇数结点则中间结点为1个。

AC代码:

class Solution {
		vector<int> G[20010];
		int cnt[20010]; //记录度（无向图的度为出度入读和，只算一者）
	public:
		vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
			for(int i=0; i<edges.size(); i++) {
				int u=edges[i][0],v=edges[i][1];
				G[u].push_back(v);
				G[v].push_back(u);
				cnt[u]++;//记录度
				cnt[v]++;
			}
			queue<int> q;
			for(int i=0; i<n; i++)
				if(cnt[i]==1) q .push(i);//将度为1的结点加入队列
			while(n>2) {//当剔除后剩下的结点数小于等于2时候结束
				int size=q.size();
				n-=size;
				while(size--) {
					int now=q.front();
					q.pop();
					for(int i=0; i<G[now].size(); i++) {//将当前度为1的结点剔除 并且其所连接的结点的度-1
						cnt[G[now][i]]--;
						if(cnt[G[now][i]]==1) q.push(G[now][i]);//如果是叶子结点加入队列
					}
				}
			}
			vector<int> ans;
			while(!q.empty()) {//已经取得了最后一层的结果结点导入结果数组
				ans.push_back(q.front());
				q.pop();
			}
			if(ans.size()==0) ans.push_back(0);//单独处理一个结点的情况
			return ans;
		}
};