PAT A1066 Root of AVL Tree (25 分)

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

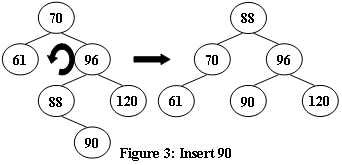
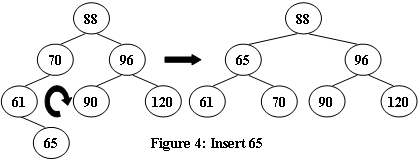
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

实现思路：

AVL平衡二叉树的模板题，记住然后建树返回根节点的值即可，主要是 插入后四种需要调整的情况不详细赘述。

AC代码：

#include <iostream>
#include <cmath>
using namespace std;
struct node {
	int data,height;
	node *l,*r;
};


int getHeight(node *root) {//获取当前结点的高度 
	return root==NULL?0:root->height;
}

void updateHeight(node *&root) {//更新当前结点的高度 
	root->height=max(getHeight(root->l),getHeight(root->r))+1;
}

int getBalanceFac(node *root) {//获取当前父节点的平衡因子 
	return getHeight(root->l)-getHeight(root->r);
}

void L(node *&root) { 
	node *temp=root->r;
	root->r=temp->l;
	temp->l=root;
	updateHeight(root);//调整后需要调整子树和父节点的高度 
	updateHeight(temp);
	root=temp;
}

void R(node *&root) {
	node *temp=root->l;
	root->l=temp->r;
	temp->r=root;
	updateHeight(root);
	updateHeight(temp);
	root=temp;
}

void insert(node *&root,int x) {
	if(root==NULL) {
		root=new node;
		root->data=x;
		root->height=1;//设置叶结点的高度 
		root->l=root->r=NULL;
		return;
	}
	if(x<root->data) {
		insert(root->l,x);
		updateHeight(root);//插入结点后需要进行子树高度调整 
		if(getBalanceFac(root)==2) {
			if(getBalanceFac(root->l)==1) {
				R(root); 
			} else if(getBalanceFac(root->l)==-1) {
				L(root->l);
				R(root);
			}
		}
	} else {
		insert(root->r,x);
		updateHeight(root);
		if(getBalanceFac(root)==-2) {
			if(getBalanceFac(root->r)==-1) {
				L(root);
			} else if(getBalanceFac(root->r)==1) {
				R(root->r);
				L(root);
			}
		}
	}
}


int main() {
	node *root=NULL;
	int n,val;
	cin>>n;
	while(n--) {
		scanf("%d",&val);
		insert(root,val);
	}
	cout<<root->data;
	return 0;
}