图神经网络——GCN聚合原理理解

本博客基于B站UP主望舒同学的图神经网络系列讲解及代码实现-GCN1。

GCN的核心思想：通过邻接矩阵A对结点特征进行聚合，用于更新某结点特征。不同的聚合方式\(\rightarrow\) GCN变体。

GCN基于的一个假设：结点的特征与其邻居结点有密切的关系，并且距离越近的邻居关系越大。

GCN聚合直接邻居结点

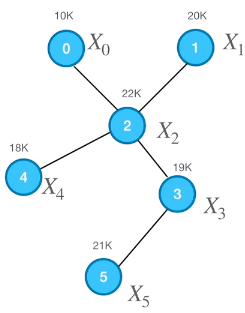
这是一个简单的图结构。笔者将以该图为示例，讲解GCN以最简单的方式（求平均）聚合直接邻居结点流程。由上图结构可知，其邻接矩阵为\(A = \begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ \end{pmatrix}\)，结点特征\(X = \begin{pmatrix} X_0 \\ X_1 \\ X_2 \\ X_3 \\ X_4 \\ X_5 \end{pmatrix} = \begin{pmatrix} 10 \\ 20 \\ 22 \\ 19 \\ 18 \\ 21 \end{pmatrix}\)，度矩阵\(D = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{pmatrix}\)。

Step 1——求和

以\(X_2\)为更新对象。注意：\(A_i\)表示邻接矩阵的第\(i\)行，\(A_{ij}\)表示邻接矩阵的第\(i\)行第\(j\)列。

\[\begin{align} aggregate(X_2) & = X_0 + X_1 + X_3 + X_4 \nonumber \\ & = 1 \cdot X_0 + 1 \cdot X_1 + 0 \cdot X_2 + 1 \cdot X_3 + 1 \cdot X_4 + 0 \cdot X_5 \nonumber \\ & = A_2 X \end{align} \]

虽然这样更新了\(X_2\)，但是没有包含其本身的特征。总不能全部依靠邻居的特征吧，显得不太合理。因此，加上自身的特征，相当于自环。\(\hat{A} = A + I = \begin{pmatrix} 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ \end{pmatrix}\)，\(I\)为单位矩阵。

则（1）式修改为

\[\begin{align} aggregate(X_2) & = X_0 + X_1 + X_2 + X_3 + X_4 \nonumber \\ & = 1 \cdot X_0 + 1 \cdot X_1 + 1 \cdot X_2 + 1 \cdot X_3 + 1 \cdot X_4 + 0 \cdot X_5 \nonumber \\ & = \hat{A_2} X \end{align} \]

Step 2——求平均

因为\(\hat{A}\)考虑到了自身特征，所以\(\hat{D} = D + I\)。

\[\begin{align} aggregate(X_2) & = \frac{X_0 + X_1 + X_2 + X_3 + X_4}{5} \nonumber \\ & = \frac{1 \cdot X_0 + 1 \cdot X_1 + 1 \cdot X_2 + 1 \cdot X_3 + 1 \cdot X_4 + 0 \cdot X_5 }{5} \nonumber \\ & = \frac{\hat{A_2} X}{5} \nonumber \\ & = \frac{\hat{A_2} X}{\hat{D}_{2,2}} \nonumber \\ & = \hat{D}_{2,2}^{-1}\hat{A_2} X \end{align} \]

整体计算如下：

\[\begin{equation} aggregate(X) = \hat{D}^{-1} \hat{A} X \end{equation} \]

注意：\(\hat{D}\)是对角阵，因此左乘和右乘结果相同，并且其逆等于对角线元素值的倒数。

（4）式其实相当于使用了一种归一化方法，即非对称归一化邻接矩阵，目的是消除结点度数对聚合信息的影响。详见图神经网络知识总结——归一化。也可以采用其他方式求平均方式或称为归一化方式，如对称归一化邻接矩阵、归一化拉普拉斯矩阵等。

Step 3——更新

将求平均后的值作为聚合后的特征值。

GCN聚合间接邻居结点

实际操作：在第一次卷积的基础上，以相同的方式，进行第二次卷积，第三次卷积 ……

理解：第一次卷积之后，结点特征已经聚合了其直接邻居结点的特征，所以再一次进行卷积的时候，虽然看上去还是在对直接邻居结点进行卷积，但是相当于在对其邻居的邻居结点（间接邻居结点）进行卷积。