Perceptron感知机
感知机：权衡输入的因素，做出决策。同时，能做出逻辑判断，并、或、异或。
单个感知机
- 输入\(x_i\)，依据各自的权重，计算出输出。
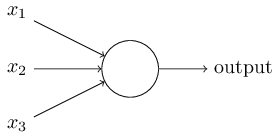
- 根据阈值，判断输出是1还是0。
\[output =
\begin{cases}
0, &{if }\sum_j w_jx_j \leq threshold \\
1, &{if }\sum_j w_jx_j \geq threshold
\end{cases}
\]
以上就是感知机的大致流程。
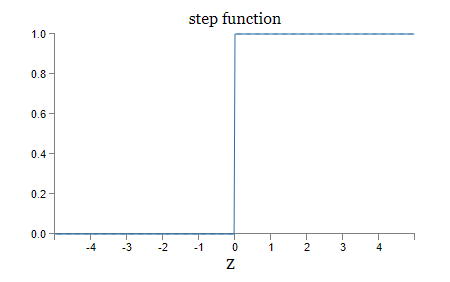
注意：最后感知机经过了threshold后输出0或者1，这里相当于使用了step function（跃阶函数）作为了激活函数。该函数不可导，不可微，所以不利于进行参数更新。这里仅是为了理解感知机更简单。
形象例子
假设，你听说这周末在你的城市将会举办奶酪节。你喜欢奶酪，然后在考虑是否要去奶酪节。你要权衡以下三个因素：
- 是否是个好天？
- 你的对象是否会陪你一起？
- 奶酪节附件有没有公共交通？（假设你没有车）
用二进制表示这些输入。\(x_i\)表示第i个因素，如果为1，表示是天气好或者对象会陪你或者有公共交通；如果为0，则相反。
假设，你自己十分想去奶酪节，无论对象想不想去，无论周围是否有公共交通，你都想去。那么可以将权重设置为\(w_1 = 6、w_2 = 2、w_3 = 2\)，然后阈值设置为5。也就意味着只要天气好，你就会去。可以通过改变权值和阈值，得到不同的决策模型。 阈值越低，表明你越想去参加奶酪节；某个因素的权重越高，表明该因素越重要。
多层感知机
一个感知机肯定不是一个彻底的人类决策模型。但是，越复杂的感知机网络可以做出更加精秒的决策。
简单理解：将输入向量赋予不同的权重向量，整合后加起来（多项式求和），并通过激活函数输出1或-1。
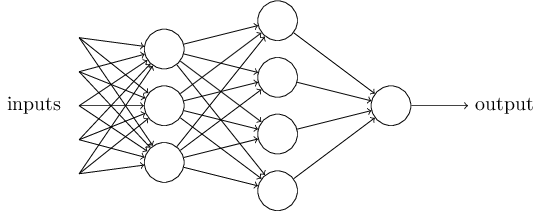
- 第一层感知机有三个感知机。通过对输入加权，这一层可以做出三个简单的决策。
- 第一层的输出是第二层感知机（4个感知机）的输入。这样，第二层的感知机可以做出更加复杂，更加抽象的决策。
- 这样，多层感知机后，就可以做出更加复杂的决策。
简化表示方式
对$\sum_j w_jx_J > threshold $ 做出两个变化：
- 将\(\sum_j w_j x_j\)表示为向量点乘\(w\cdot x\)。
解释：\(\sum_j w_j x_j = w_1x_1 +w_2x_2+w_3x_3+...+w_jx_j\)。转念一想这和矩阵乘法如出一辙。这就相当于
\[\sum_j w_jx_j = \left(
\begin{matrix}
w_1 & w_2 & w_3 & ... & w_j
\end{matrix}
\right)
\cdot
\left(
\begin{matrix}
x_1 \\
x_2 \\
x_3 \\
. \\
. \\
. \\
x_j
\end{matrix}
\right)
\]
- $\sum_j w_jx_J > threshold $ 将阈值从不等式的右边，移到左边，作为bias偏置，即\(b = -threshold\)
简化后:
\[output =
\begin{cases}
0, &{if }\quad w \cdot x + b \leq 0 \\
1, & {if}\quad w \cdot x + b \geq 0
\end{cases}
\]
偏置bias的含义是：感知机能多么轻易输出1。如果bias很大，那么很容易整体值就大于0，则输出1了。如果bias是负，则整体值要很大才能大于0，最终才能输出1。
模型训练过程就是通过学习算法，自动地调节神经网络的权重和偏置。
