17.树

1.知识框图

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Real_Fool_/article/details/113930623

2.树的基本概念

树状图是一种数据结构，它是由n（n>=1）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

每个节点有零个或多个子节点；没有父节点的节点称为根节点；每一个非根节点有且只有一个父节点；除了根节点外，每个子节点可以分为多个不相交的子树；

专业术语	中文	描述
Root	根节点	一棵树的顶点
Child	孩子节点	一个节点含有的子树的根节点称为该节点的子节点
Leaf	叶子节点	没有孩子的节点
Degree	度	一个节点包含的子树的数量
Edge	边	一个节点与另外一个节点的连接
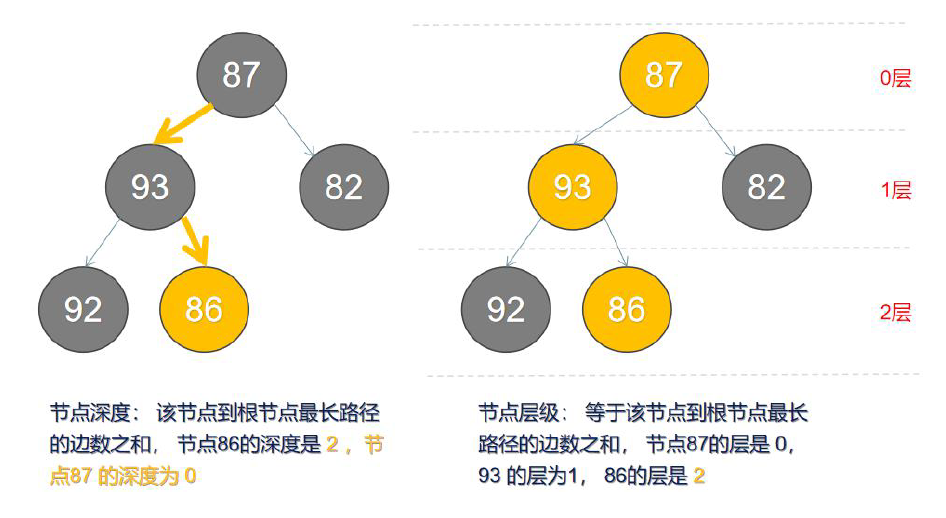
Depth	深度	根节点到这个节点经过的边的数量
Height	节点高度	从当前节点到叶子节点形成路径中边的数量
Level	层级	节点到根节点最长路径的边的总和
Path	路径	一个节点和另一个节点之间经过的边和Node 的序列

3.二叉树的原理精讲

我们以前介绍的线性表一样，一个没有限制的线性表应用范围可能有限，但是我们对线性表进行一些限制就可以衍生出非常有用的数据结构如栈、队列、优先队列等。

树也是一样，一个没有限制的树由于太灵活，控制起来比较复杂。如果对普通的树加上一些人为的限制，比如节点只允许有两个子节点，这就是我们接下来要介绍的二叉树。

二叉树是一个每个节点最多只能有两个分支的树，左边的分支称之为左子树，右边的分支称之为右子树。

(1) 在非空二叉树中，第i-1层的节点总数不超过，2^(i-1)，i>=1； 
(2) 深度为h-1 的二叉树最多有个节点(h>=1)，最少有2^h-1个节点； 
(3) 对于任意一棵二叉树，如果其叶节点数为N0，而度数为2 的节点总数为N2，则N0=N2+1；

3.1常见二叉树分类：

（1）完全二叉树---若设二叉树的高度为h，除第h层外，其它各层(1～h-1) 的结点数都达到最大个数，第h层有叶子节点，并且叶子结点都是从左到右依次排布，这就是完全二叉树（堆就是完全二叉树）。

（2）满二叉树---除了叶结点外每一个结点都有左右子节点且叶子结点都处在最底层的二叉树。

（3）平衡二叉树---又被称为AVL树，它是一棵空树或左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

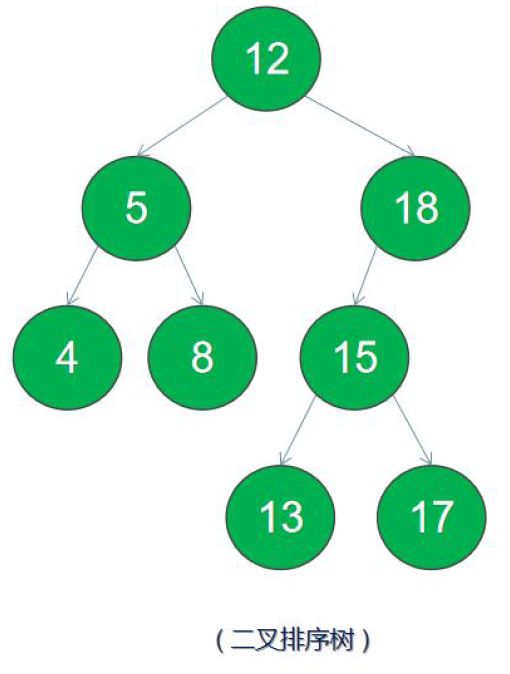
（4）二叉搜索树---又称二叉查找树、二叉排序树（Binary Sort Tree）。它是一颗空树或是满足下列性质的二叉树：
1）若左子树不空，则左子树上所有节点的值均小于或等于它的根节点的值；
2）若右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值；
3）左、右子树也分别为二叉排序树。

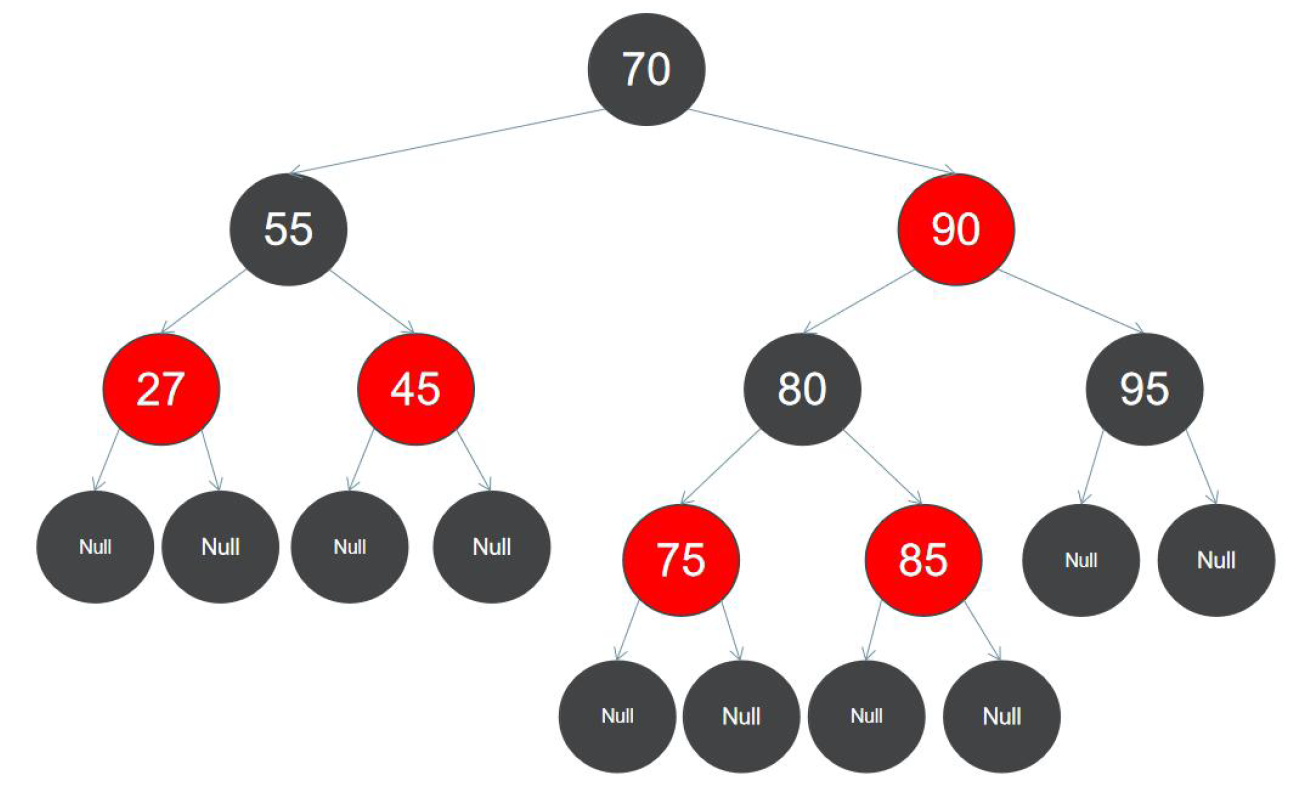
（5）红黑树---是每个节点都带有颜色属性（颜色为红色或黑色）的自平衡二叉查找树，满足下列性质：
1）节点是红色或黑色；
2）根节点是黑色；
3）所有叶子节点都是黑色；
4）每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
5）从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

4.二叉搜索树的算法实现

1.当我们要在一组数中要找到你女朋友（或未来女朋友）的年龄，比如26？你该怎么找？

答案： 从左至右或从右至左遍历一次，找到这个数字

2.当我们把数据进行排序（按照从小到大的顺序排列）后，再查找相应的这条记录？还是用上面的方法吗？

答案：最快的方式，是采用折半法（俗称二分查找）

思考：当我们有新的数据加进来，或者删除其中的一条记录，为了保障查找的效率，我们仍然要保障数组有序，但是，会碰到我们讲顺序表时的问题，涉及到大量数据的移动！在插入和删除操作上，就需要耗费大量的时间（需进行元素的移位），能否有一种既可以使得插入和删除效率不错，又可高效查找的数据结构和算法呢？
抛砖: 首先解决一个问题，插入时不移动元素，我们可以想到链表，但是要保证其有序的话，首先得遍历链表寻找合适的位置，那么又如何高效的查找合适的位置呢，能否可以像二分一样，通过一次比较排除一部分元素？
引玉： 那么我们可以用二叉树的形式，以数据集第一个元素为根节点，之后将比根节点小的元素放在左子树中，将比根节点大的元素放在右子树中，在左右子树中同样采取此规则。那么在查找x时，若x比根节点小可以排除右子树所有元素，去左子树中查找（类似二分查找），这样查找的效率非常好，而且插入的时间复杂度为O(h)，h为树的高度，较O(n)来说效率提高不少。故二叉搜索树用作一些查找和插入使用频率比较高的场景。

二叉树一般采用链式存储方式：每个结点包含两个指针域，指向两个孩子结点，还包含一个数据域，存储结点信息。

4.1节点结构体的定义

#define MAX_NODE 1024

#define isLess(a, b) (a<b)
#define isEqual(a, b) (a==b)

typedef int ElemType;//元素类型

typedef struct _Bnode
{
    ElemType data;//节点存储的数据
    struct Bnode *lchild, *rchild;//指向左右孩子节点
}Bnode, Btree;

4.2二叉搜索树插入节点

将要插入的结点e，与节点root节点进行比较，若小于则去到左子树进行比较，若大于则去到右子树进行比较，重复以上操作直到找到一个空位置用于放置该新节点。

bool InsertBtree(Btree** root, Bnode* node)
{
	Bnode* tmp = NULL;
	Bnode* parent = NULL;

	if (!node)
	{
		return false;
	}
	else//清空新节点的左右子树
	{
		node->lchild = NULL;
		node->rchild = NULL;
	}

	if (*root)//存在根节点
	{
		tmp = *root;
	}
	else//不存在根节点
	{
		*root = node;
		return true;
	}

	while (tmp != NULL)
	{
		parent = tmp;//保存父节点
		//printf("父节点：%d\n", parent->data);
		if (isLess(node->data, tmp->data))
			tmp = tmp->lchild;
		else
			tmp = tmp->rchild;
	}

	if (isLess(node->data, parent->data))
		parent->lchild = node;
	else
		parent->rchild = node;

	return true;
}

4.3二叉搜索树删除节点

将要删除的节点的值，与节点root节点进行比较，若小于则去到左子树进行比较，若大于则去到右子树进行比较，重复以上操作直到找到一个节点的值等于删除的值，则将此节点删除。删除时有4中情况须分别处理：

■删除节点不存在左右子节点，即为叶子节点，直接删除

■删除节点存在左子节点，不存在右子节点，直接把左子节点替代删除节点

■删除节点存在右子节点，不存在左子节点，直接把右子节点替代删除节点

■删除节点存在左右子节点，则取左子树上的最大节点或右子树上的最小节点替换删除节点

代码实现：

/************************
* 采用递归方式查找结点
*************************/
/*
其中，root是树根节点指针，key是要删除的节点的关键字。

函数的执行流程如下：

如果根节点为空，直接返回空指针，表示没有找到要删除的节点。
如果根节点的关键字大于要删除的节点的关键字，递归调用 DeleteNode 函数来删除左子树中的节点。如果成功删除了左子树中的节点，返回根节点指针。
如果根节点的关键字小于要删除的节点的关键字，递归调用 DeleteNode 函数来删除右子树中的节点。如果成功删除了右子树中的节点，返回根节点指针。
如果根节点的关键字等于要删除的节点的关键字，继续检查其左右子节点是否存在。
如果左右子节点都为空，直接返回空指针，表示成功删除了该节点。
如果只存在右子节点，用右子节点取代根节点，并返回根节点指针。
如果只存在左子节点，用左子节点取代根节点，并返回根节点指针。
如果左右子节点都存在，用左子节点的最大值来替换根节点的值，并递归调用 DeleteNode 函数来删除左子树中这个最大值对应的节点。最后返回根节点指针。
这个函数的目的是在B树中删除一个给定关键字的节点，同时保持B树的平衡性质。
*/
Btree* DeleteNode(Btree* root, int key) 
{
	if (root == NULL)return NULL;//没有找到删除节点
	if (root->data > key)
	{
		root->lchild = DeleteNode(root->lchild, key);
		return root;
	}
	if (root->data < key)
	{
		root->rchild = DeleteNode(root->rchild, key);
		return root;
	}
	//删除节点不存在左右子节点，即为叶子节点，直接删除
	if (root->lchild == NULL && root->rchild == NULL)return NULL;
	//删除节点只存在右子节点，直接用右子节点取代删除节点
	if (root->lchild == NULL && root->rchild != NULL)return root->rchild;
	//删除节点只存在左子节点，直接用左子节点取代删除节点
	if (root->lchild != NULL && root->rchild == NULL)return root->lchild;
	////删除节点存在左右子节点，直接用左子节点最大值取代删除节点
	int val = findMax(root->lchild);
	root->data = val;
	root->lchild = DeleteNode(root->lchild, val);
	return root;
}

4.4二叉搜索树搜索

/************************
* 采用递归方式查找结点
*************************/
Bnode* queryByRec(Btree *root, ElemType e)
{
    if (root == NULL || isEqual(root->data, e))
    {
        return root;
    } 
    else if(isLess(e, root->data)) 
    {
        return queryByRec(root->lchild, e);
    } 
    else
    {
        return queryByRec(root->rchild, e);
    }
}

/**
* 使用非递归方式查找结点
*/
Bnode* queryByLoop(Bnode *root, int e)
{
    while(root != NULL && !isEqual(root->data, e))
    {
        if(isLess(e, root->data))
        {
            root = root->lchild;
       }
        else
        {
            root = root->rchild;
        }
    }
    return root;
}

4.5二叉树的遍历

二叉树的遍历是指从根结点出发，按照某种次序依次访问所有结点，使得每个结点被当且访问一次。共分为四种方式：
前序遍历- 先访问根节点，然后前序遍历左子树，再前序遍历右子树

上图前序遍历结果： 19 7 5 11 15 25 21 61

●前序遍历- 递归实现

/************************
* 采用递归方式实现前序遍历
*************************/
void PreOrderRec(Btree* root)
{
	if (root == NULL)
	{
		return;
	}
	printf("- %d -", root->data);
	PreOrderRec(root->lchild);
	PreOrderRec(root->rchild);
}

●前序遍历 - 非递归方式实现
具体过程：
首先申请一个新的栈，记为stack；
将头结点head压入stack 中；
每次从stack中弹出栈顶节点，记为cur，然后打印cur值，如果cur 右孩子不为空，则将右孩子压入栈中；如果cur 的左孩子不为空，将其压入stack 中；
重复步骤3，直到stack 为空。
参考资料来源：

奇牛学院