19.图
1.图的原理精讲
在计算机科学中,一个图就是一些顶点的集合,这些顶点通过一系列边结对(连接)。顶点用圆圈表示,边就是这些圆圈之间的连线。顶点之间通过边连接。注意:顶点有时也称为节点或者交点,边有时也称为链接。
社交网络,每一个人就是一个顶点,互相认识的人之间通过边联系在一起, 边表示彼此的关系。这种关系可以是单向的,也可以是双向的!
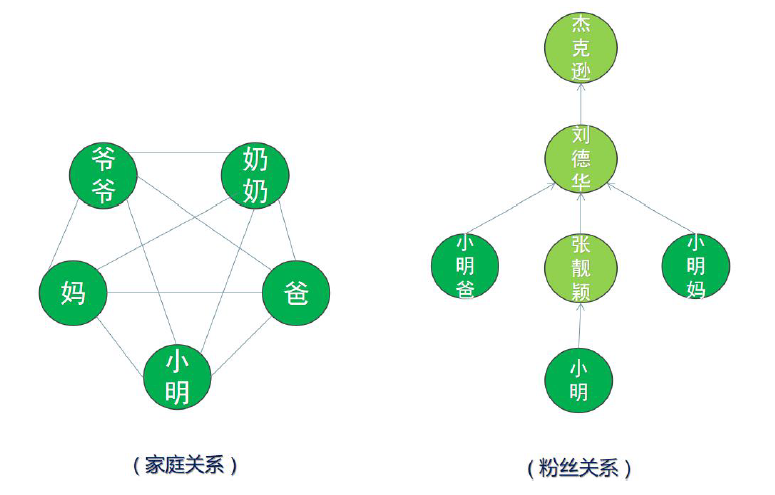
同时,边可以是双向的,也可以是单向的!
地图导航 - 起点、终点和分叉口(包括十字路口、T字路口等)都是顶点,导航经过的两顶点的路径就是边!
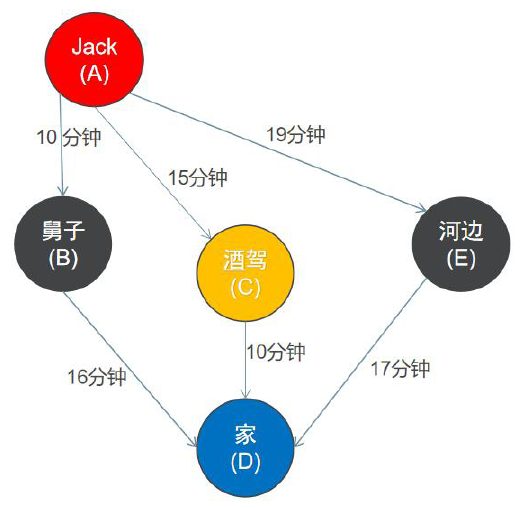
我们导航从一个点到另外一个点可以有条路径,路径不同,路况就不同,拥堵程度不同,所以导致不同路径所花的时间也不一样,这种不同我们可以使用边的权重来表示,即根据每条边的实际情况给每一条边分配一个正数或者负数值。考虑如下机票图,各个城市就是顶点,航线就是边。那么权重就是机票价格。
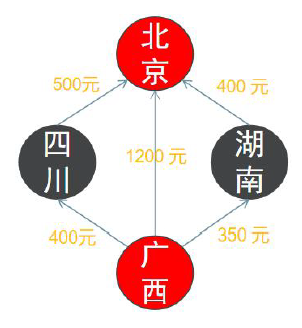
树和链表都是图的特例!
如果我们有一个编程问题可以通过顶点和边表示,那么我们就可以将你的问题用图画出来,然后使用相应的图算法来找到解决方案。
1.1图的表示
1.1.1邻接列表
在邻接列表实现中,每一个顶点会存储一个从它这里开始的相邻边的列表。比如,如果顶点B有一条边到A、C 和E,那么A 的列表中会有3 条边
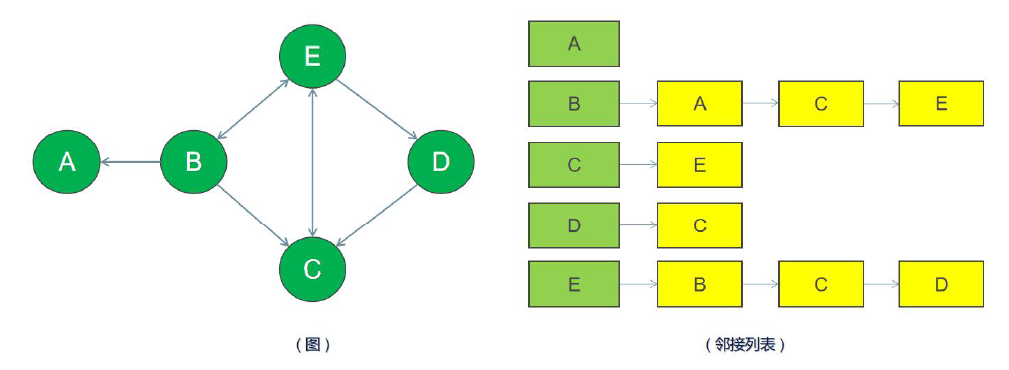
邻接列表只描述指向外部的边。B有一条边到 A,但是A没有边到B,所以B没有出现在A的邻接列表中。查找两个顶点之间的边或者权重会比较费时,因为遍历邻接列表直到找到为止。
1.1.2邻接矩阵
由二维数组对应的行和列都表示顶点,由两个顶点所决定的矩阵对应元素数值表示这里两个顶点是否相连(如,0 表示不相连,非0表示相连和权值)、如果相连这个值表示的是相连边的权重。例如,广西到北京的机票,我们用邻接矩阵表示:
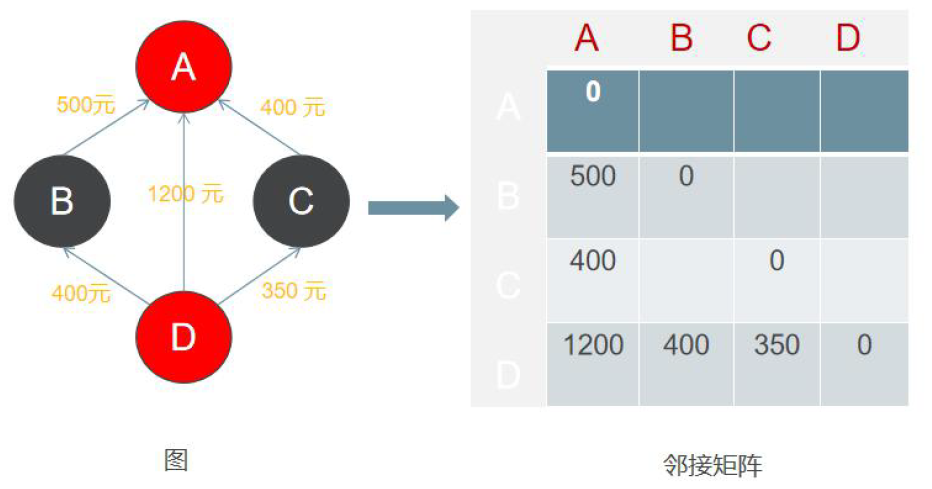
往这个图中添加顶点的成本非常昂贵,因为新的矩阵结果必须重新按照新的行/列创建,然后将已有的数据复制到新的矩阵中。
所以使用哪一个呢?我们先来看看下表
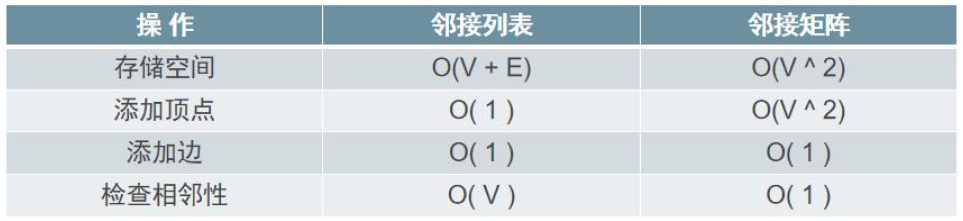
注意: V 表示图中顶点的个数,E 表示边的个数。
结论:大多数时候,选择邻接列表是正确的。(在图比较稀疏的情况下,每一个顶点都只会和少数几个顶点相连,这种情况下邻接列表是最佳选择。如果这个图比较密集,每一个顶点都和大多数其他顶点相连,那么邻接矩阵更合适。)
2.图的算法实现
2.1邻接表结构的定义
思路:先把节点的数据保存在图中,用时从中提取
#define MaxSize 1024
typedef struct _EdgeNode//边与节点连接的边的定义
{
int adjvex;//邻接顶点的下标
int weight;//权重
struct _EdgeNode* next;//下一条边
}EdgeNode;
typedef struct _VertexNode//顶点节点
{
char data;//节点数据
struct _EdgeNode* first;//指向邻接的第一条边
}VertexNode,AdjList;
typedef struct _AdjListGraph
{
AdjList* adjlist;
int vex;//顶点数
int edge;//边数
}AdjListGraph;
2.2邻接表的初始化
//图的初始化
void Init(AdjListGraph& G)
{
G.adjlist = new AdjList[MaxSize];
G.edge = 0;
G.vex = 0;
}
2.3邻接表的创建
//图的创建
void Create(AdjListGraph& G)
{
//第一步:先把所有图的顶点数据、边数保存在图中
cout << "请输入该图的顶点数及边数:" << endl;
cin >> G.vex >> G.edge;
cout << "请输入相关的顶点:" << endl;
for (int i = 0; i < G.vex; i++)
{
cin >> G.adjlist[i].data;
G.adjlist[i].first = NULL;//所有顶点指向的邻接第一条边为空
}
char v1 = 0, v2 = 0;//保存输入的顶点的字符
int i1, i2;//保存顶点在数组中的下标
//第二步:建立顶点和与其关联的下一个顶点之间的联系
cout << "请输入相关联的顶点:" << endl;
for (int i = 0; i < G.edge; i++)
{
cin >> v1 >> v2;
i1 = Location(G, v1);
i2 = Location(G, v2);
if (i1 != -1 && i2 != -1)//寻找到位置了
{
EdgeNode* temp = new EdgeNode;//新创建一条边
temp->adjvex = i2;
temp->next = G.adjlist[i1].first;//G.adjlist[i1]表示第i1个顶点,G.adjlist[i1].first表示第i1个顶点指向邻接的第一条边
G.adjlist[i1].first = temp;//将G.adjlist[i1].first指向的边改为新创建的边temp
}
}
}
2.4邻接表的深度遍历
深度优先遍历思想:
▶首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点;
▶ 当没有未访问过的顶点时,则回到上一个顶点,继续试探别的顶点,直到所有的顶点都被访问过。
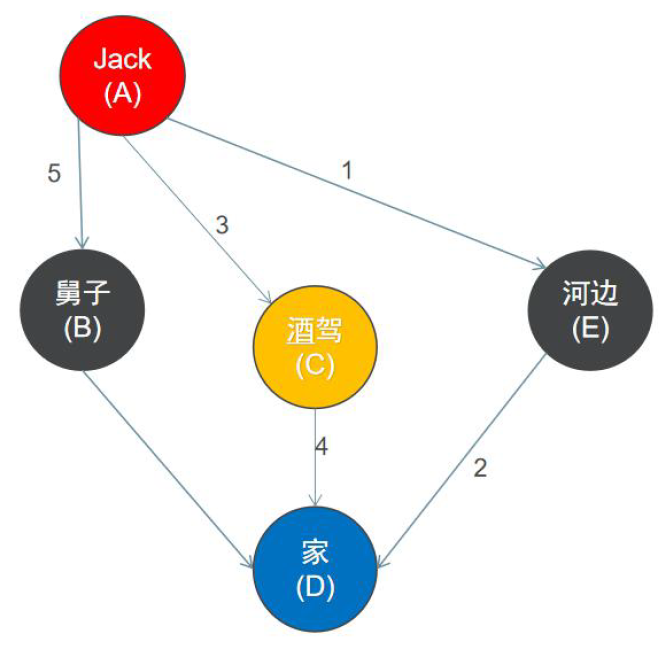
使用深度优先搜索来遍历这个图的具体过程是:
1. 首先从一个未走到过的顶点作为起始顶点,比如A顶点作为起点。
2. 沿A顶点的边去尝试访问其它未走到过的顶点,首先发现E号顶点还没有走到过,于是访问E顶点。
3. 再以E顶点作为出发点继续尝试访问其它未走到过的顶点,接下来访问D顶点。
4. 再尝试以D顶点作为出发点继续尝试访问其它未走到过的顶点。
5. 但是,此时沿D顶点的边,已经不能访问到其它未走到过的顶点,接下来返回到E顶点。
6. 返回到E顶点后,发现沿E顶点的边也不能再访问到其它未走到过的顶点。此时又回到顶点A(D->E->A),再以A
顶点作为出发点继续访问其它未走到过的顶点,于是接下来访问C顶点。
7. 。。。。。。。。。。
8. 最终访问的结果是A -> E -> D -> C -> B
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
#define MaxSize 1024
typedef struct _EdgeNode//边与节点连接的边的定义
{
int adjvex;//邻接顶点的下标
int weight;//权重
struct _EdgeNode* next;//下一条边
}EdgeNode;
typedef struct _VertexNode//顶点节点
{
char data;//节点数据
struct _EdgeNode* first;//指向邻接的第一条边
}VertexNode,AdjList;
typedef struct _AdjListGraph
{
AdjList* adjlist;
int vex;//顶点数
int edge;//边数
}AdjListGraph;
bool visited[MaxSize];//全局数组,用来记录节点是否已被访问
int Location(AdjListGraph& G, char c);
//图的初始化
void Init(AdjListGraph& G)
{
G.adjlist = new AdjList[MaxSize];
G.edge = 0;
G.vex = 0;
for (int i = 0; i < MaxSize; i++)
{
visited[i] = false;
}
}
//图的创建
void Create(AdjListGraph& G)
{
//第一步:先把所有图的顶点数据、边数保存在图中
cout << "请输入该图的顶点数及边数:" << endl;
cin >> G.vex >> G.edge;
cout << "请输入相关的顶点:" << endl;
for (int i = 0; i < G.vex; i++)
{
cin >> G.adjlist[i].data;
G.adjlist[i].first = NULL;//所有顶点指向的邻接第一条边为空
}
char v1 = 0, v2 = 0;//保存输入的顶点的字符
int i1, i2;//保存顶点在数组中的下标
//第二步:建立顶点和与其关联的下一个顶点之间的联系
cout << "请输入相关联的顶点:" << endl;
for (int i = 0; i < G.edge; i++)
{
cin >> v1 >> v2;
i1 = Location(G, v1);
i2 = Location(G, v2);
if (i1 != -1 && i2 != -1)//寻找到位置了
{
EdgeNode* temp = new EdgeNode;//新创建一条边
temp->adjvex = i2;
temp->next = G.adjlist[i1].first;//G.adjlist[i1]表示第i1个顶点,G.adjlist[i1].first表示第i1个顶点指向邻接的第一条边
G.adjlist[i1].first = temp;//将G.adjlist[i1].first指向的边改为新创建的边temp
}
}
}
//对图上的顶点进行深度遍历
void DFS(AdjListGraph& G, int v)
{
int next = -1;//下一个结点下标
if (visited[v]) return;
cout << G.adjlist[v].data << " ";
visited[v] = true;//设置为已访问
EdgeNode* temp = G.adjlist[v].first;//访问边
while (temp)
{
next = temp->adjvex;//获取下一个结点下标
temp = temp->next;//获取下一条边 此时的next和temp->next中的next不是一个东西
if (visited[next] == false)
{
DFS(G, next);
}
}
}
//对所有顶点进行深度遍历
void DFS_Main(AdjListGraph& G)//遍历顺序和图保存的数据顺序有关,第一个数据是最先存入的
{
for (int i = 0; i < G.vex; i++)
{
if (visited[i] == false)
{
DFS(G, i);
}
}
}
int main()
{
AdjListGraph G;
//初始化
Init(G);
//创建图
Create(G);
//深度遍历
DFS_Main(G);
system("pause");
return EXIT_SUCCESS;
}
//寻找顶点对应的字符寻找顶点在图中的邻节点
int Location(AdjListGraph& G, char c)
{
for (int i = 0; i < G.vex; i++)
{
if (G.adjlist[i].data == c)
{
return i;
}
}
return -1;
}
2.5邻接表的广度遍历
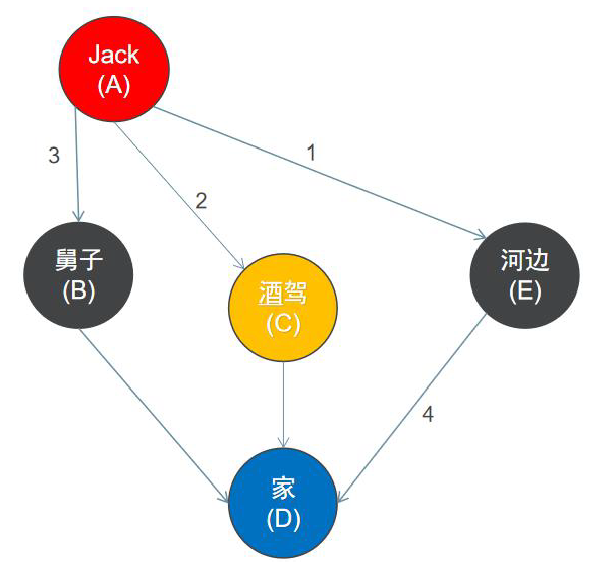
广度优先遍历思想
▶首先以一个未被访问过的顶点作为起始顶点,访问其所有相邻的顶点;
▶然后对每个相邻的顶点,再访问它们相邻的未被访问过的顶点,直到所有顶点都被访问过,遍历结束。
//对图上的顶点进行广度遍历
void BFS(AdjListGraph& G, int v)
{
queue<int> q;
int cur = -1;
int index = -1;
q.push(v);
while (!q.empty())//队列非空
{
cur = q.front();//队列头元素
if (visited[cur] == false)//当前的顶点还没有被访问
{
cout << G.adjlist[cur].data << " ";
visited[cur] = true;
}
q.pop();//出队列
EdgeNode* temp = G.adjlist[cur].first;
while (temp != NULL)
{
index = temp->adjvex;//获取下一个结点下标
temp = temp->next;//获取下一条边
q.push(index);
}
}
}
//对所有顶点进行广度遍历
void BFS_Main(AdjListGraph& G)
{
for (int i = 0; i < G.vex; i++)
{
if (visited[i] == false)
{
BFS(G, i);
}
}
}
参考资料:
奇牛学院


 浙公网安备 33010602011771号
浙公网安备 33010602011771号