四、集合结构(Set)
集合结构
集合通常是由一组无序的、不能重复的元素构成
- 和数学中的集合名次比较相似,但是数学中的集合范围更大一些,也允许集合中的元素重复
- 在计算机中,集合通常表示的结构中元素是不允许重复的
也可以把集合看成一种特殊的数组
- 特殊之处就在于里面的元素没有顺序,也不能重复
- 没有顺序意味着不能通过下标值进行访问,不能重复意味着相同的对象在集合中只会存在一份
在2015年6月份发布的ES6中包含了Set类,可以直接使用它,但是为了明确内部的实现机制,我们还是自己来封装一下这个Set类
集合中常见的操作方法:
- add(value):向集合添加一个新的项
- remove(value):从集合移除一个值
- has(value):如果值在集合中,返回true,否则返回false
- clear():清空集合中的项
- size():返回集合所包含元素的数量,与数组length相似
- values():返回一个包含集合中所有值的数组
封装集合
创建集合类
// 封装集合类
class Set {
constructor() {
// 使用一个对象保存集合的元素
this.items = {}
}
}
1.add(value)
// 向集合添加一个新的项
add(value) {
// 判断集合中是否含有此元素
if (this.has(value)) return false
// 将元素添加到集合中
this.items[value] = value
return true
}
2.remove(value)
// 删除一个元素
remove(value) {
// 判断是否含有该元素
if (!this.has(value)) return false
// 将元素从集合中删除
delete this.items[value]
return true
}
3.has(value)
// 判断集合中是否包含此元素
has(value) {
return this.items.hasOwnProperty(value)
}
4.clear()
// 清空集合
clear() {
this.items = {}
}
5.size()
// 集合长度
size() {
// Object.keys() 将对象中所以的key转变成数组
return Object.keys(this.items).length
}
6.values()
// 返回一个包含集合中所有值的数组
values() {
return Object.keys(this.items)
}
集合间操作
就是集合与集合之间的操作
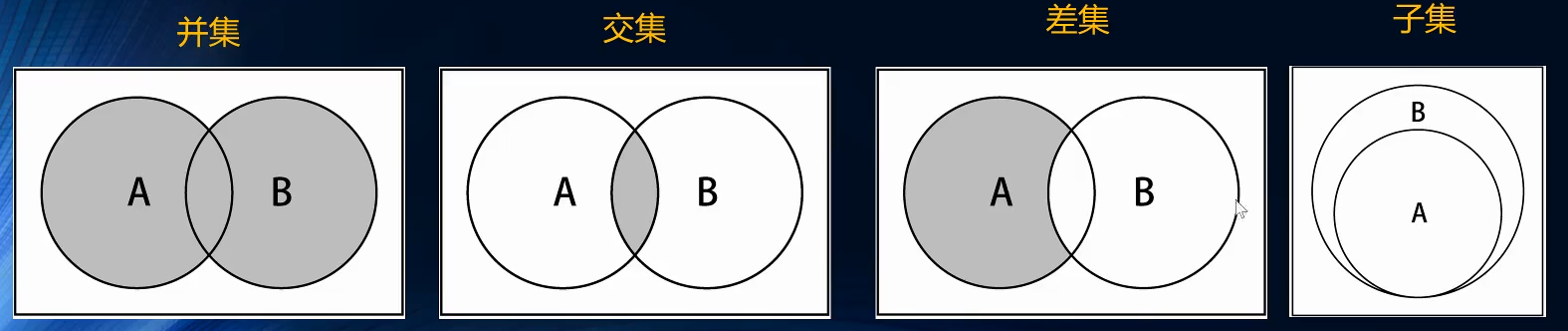
- 并集:对于给定的两个集合,返回一个包含两个集合中所有元素的集合
- 交集:对于给定的两个集合,返回一个包含两个集合中共有元素的集合
- 差集:对于给定的两个集合,返回一个包含所有存在于第一个集合且不存在于第二个集合的元素的新集合
- 子集:验证一个给定集合是否是另一集合的子集
并集实现
就是两个集合合并成一个新的集合
并集:
-
并集其实对应的就是数学中并集的概念
-
集合A和B的并集,表示为A U B ,定义如下
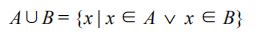
-
意思是X(元素)存在于A中,或x存在于B中
代码解析:
- 首先需要创建一个新的集合,代表两个集合的交集
- 遍历集合1中所有的值,并且添加到新集合中
- 遍历集合2中所有的值,并且添加到新集合中
- 将最终的新集合返回
代码实现
// 并集
union(otherSet) {
// this:集合对象A
// otherSet:集合对象B
// 1.创建一个新集合
const unionSet = new Set()
// 2.将A集合所以元素添加到辛几何中
this.values().forEach(val => {
unionSet.add(val)
});
// 3.取出otherSet的values,判断是否加入新集合
let values = otherSet.values()
values.forEach(val => {
// 这里不用判断新集合是否包含val,因为add方法已经做判断
unionSet.add(val)
})
// 4.将并集结果返回
return unionSet
}
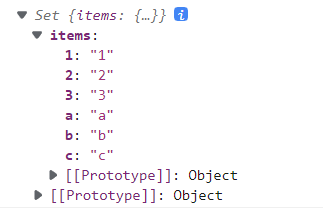
测试
const setA = new Set()
setA.add(1)
setA.add(2)
setA.add(3)
const setB = new Set()
setB.add('a')
setB.add('b')
setB.add('c')
console.log(setA.union(setB));
交集实现
交集就是两个集合中重复的元素
交集:
- 交集其实对应的就是数学中交集的概念
- 集合A和B的交集,表示为A ∩ B,定义如下
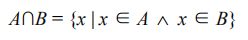
- 意思是x(元素)存在于A中,且X存在于B中
代码解析:
- 创建一个新集合
- 遍历集合1中所有的元素,判断该元素是否在集合2中
- 如果在集合2中,将该元素加入到新集合中
- 将最终的新集合返回
代码实现
// 交集
intersection(otherSet) {
// this:集合对象A
// otherSet:集合对象B
// 1.创建一个新集合
const newSet = new Set()
// 2.遍历集合A
this.values().forEach(val => {
// 3.判断元素是否存在于集合B,如果存在,将该元素加入到新集合
if (otherSet.has(val)) {
newSet.add(val)
}
})
// 4.最终返回新集合
return newSet
}
测试
const setA = new Set()
setA.add(1)
setA.add(2)
setA.add(3)
const setB = new Set()
setB.add('a')
setB.add('b')
setB.add('c')
setB.add(3)
console.log(setA.intersection(setB));
差集实现
集合A中的元素集合B没有包含,将没有包含的元素加入到新集合
差集
- 差集其实对应的就是数学中差集的概念
- 集合A和B的差集,表示为A -B,定义如下
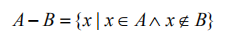
- 意思是x(元素)存在于A中,且x不存在B中
代码解析
- 创建一个新的集合
- 遍历集合1中所有的元素,判断元素是否在集合2中
- 不存在集合2中,将该元素添加到新集合中
- 将新集合返回
代码实现
// 差集
differenceSet(otherSet) {
// this:集合对象A
// otherSet:集合对象B
// 1.创建一个新集合
const newSet = new Set()
// 2.遍历集合A,判断元素是否在集合B中
this.values().forEach(val => {
if (!otherSet.has(val)) {
newSet.add(val)
}
})
// 3.返回新集合
return newSet
}
代码测试
const setA = new Set()
setA.add(1)
setA.add(2)
setA.add(3)
const setB = new Set()
setB.add('a')
setB.add('b')
setB.add('c')
setB.add(3)
console.log(setA.differenceSet(setB));
子集实现
子集:
- 子集其实对应的就是数学中子集的概念
- 集合A是B的子集(或集合B包含了A),表示为A⊆B,定义如下
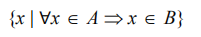
- 意思是集合A中的每一个X(元素),也需要存在于B中
代码解析:
- 遍历集合1中所有的元素,判断元素是否在集合2中
- 如果集合1中的每一个元素集合2都存在,那么集合1就是集合2的子集
代码实现
// 子集
subSet(otherSet) {
// this:集合对象A
// otherSet:集合对象B
// 1.循环集合A,查看集合B中是否含有集合A的元素
for (let i = 0; i < this.values().length; i++) {
const val = this.values()[i];
if (!otherSet.has(val)) {
// 2.如果有一个元素集合B没有,那么不是子集,返回false
return false
}
}
// 通过循环说明集合A中的元素都在集合B里包含,返回true
return true
}
代码测试
const setA = new Set()
setA.add(1)
setA.add(2)
setA.add(3)
const setB = new Set()
setB.add('a')
setB.add('b')
setB.add('c')
setB.add(3)
setB.add(2)
setB.add(1)
console.log(setA.subSet(setB)); // true


 浙公网安备 33010602011771号
浙公网安备 33010602011771号