DS博客作业05--树
1.本周学习总结
1.1思维导图

1.2谈谈你对树结构的认识及学习体会
还没有理解树之前感觉树很神秘(看过数据结构视频),树这种结构看上去很不可思议,到底是怎么实现并且操作的,学完二叉树就感觉这操作有点简单。巧妙通过递归就把对树杈的处理变成了对根和左右孩子的处理。
树可以处理大量的数据,但是对数的操作代码量不多,因为大部分操作使用了递归,需要对递归有较好的理解,否则代码很容易出现错误,而且很难发现。
树这个数据结构非常实用,所以必须要掌握,比如目录,排序等都需要树,acm也会出现树的题目。
2.PTA实验作业
2.1.题目1:6-4 jmu-ds-表达式树

2.1.1设计思路
建表达式树使用两个栈分别放树和运算符,遍历放表达式的字符串,遇到数字就建一个节点入栈,如果是运算符就要判断是否优先级,如果比栈顶小,栈顶就可以拿出来,用该运算符建一个节点,左右孩子为树栈最上面的两个节点。计算表达式,通过树的后续遍历就可以。
void InitExpTree(BTree &T, string str)
{
声明两个栈,一个树栈,一个运算符栈
Chsta.push('#')运算符栈入栈一个#号避免为空
for (遍历字符串str)
{
if (如果是数字)
{
建节点
Bt->data = str[i]
左右孩子置为空
Bt->lchild = Bt->rchild = NULL
入树栈
BTsta.push(Bt)
}
else 如果是运算符
{
调用Precede函数比较优先级
char result = Precede(Chsta.top(), str[i]);
if (如果比运算符栈栈顶大)
{
入栈
Chsta.push(str[i]);
}
else if (如果相等)说明是括号
{
出栈
Chsta.pop();
}
else 如果比运算符栈栈顶小
{
用运算符建一个节点
Bt->data = Chsta.top();
Chsta.pop();
左右孩子为树栈顶的两个
Bt->rchild = BTsta.top();
BTsta.pop();
Bt->lchild = BTsta.top();
BTsta.pop();
最后入栈
BTsta.push(Bt);
}
}
}
while (运算符栈还有运算符)
{
用运算符建一个节点
Bt->data = Chsta.top();
Chsta.pop();
左右孩子为树栈顶的两个
Bt->rchild = BTsta.top();
BTsta.pop();
Bt->lchild = BTsta.top();
BTsta.pop();
最后入栈
BTsta.push(Bt);
}
}
double EvaluateExTree(BTree T)
{
double left, right放左孩子和右孩子
if (T == NULL)
{
return 0;
}
if (如果是叶子节点)
{
return T->data-'0' 返回节点值
}
递归左孩子
left = EvaluateExTree(T->lchild);
递归右孩子
right = EvaluateExTree(T->rchild);
计算
switch (T->data) // 根据b结点做相应运算
{
case '+':
return left + right;
case '-':
return left - right;
case '*':
return left * right;
case '/':
if (right != 0)
return left / right;
else
{
cout<<"divide 0 error!"; // 除0异常退出
exit(0);
}
}
}
2.1.2代码截图
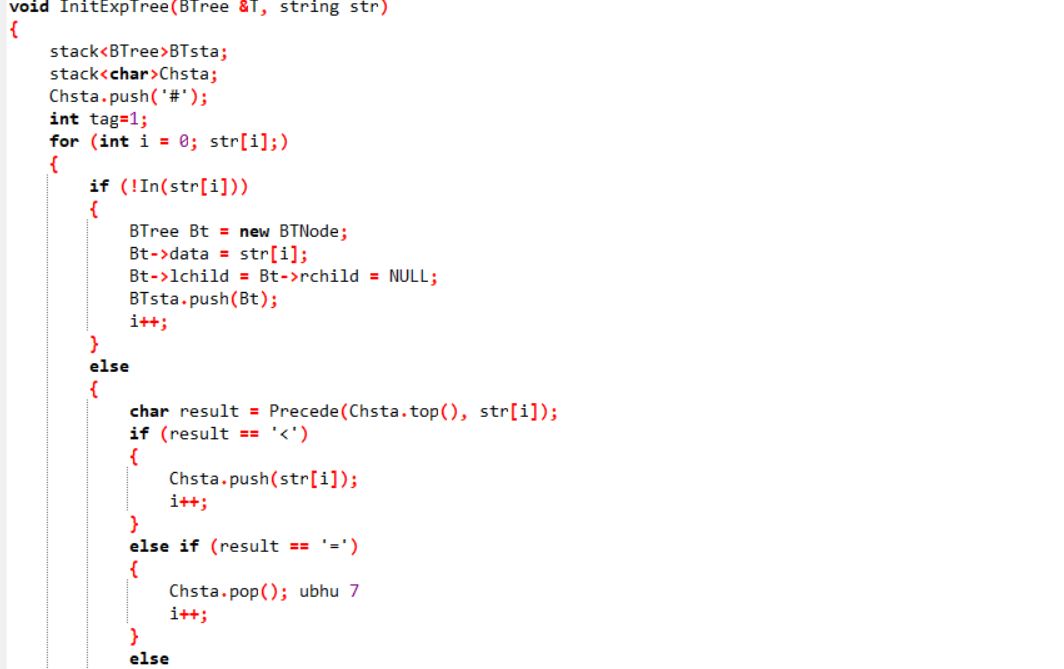
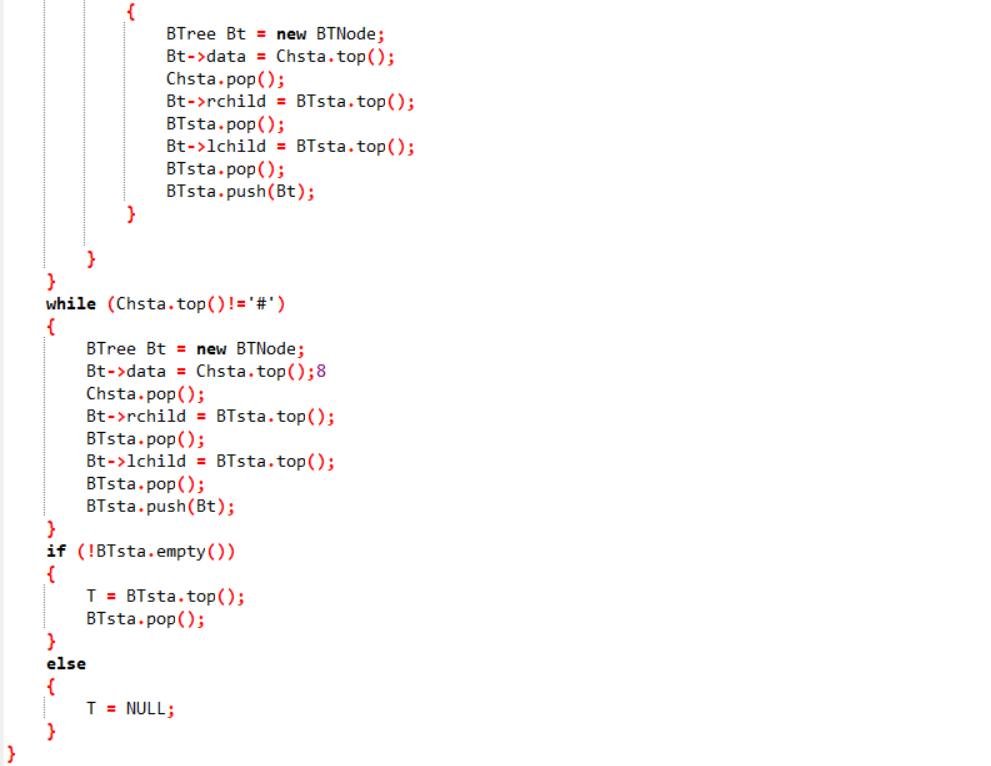

2.1.3本题PTA提交列表说明

Q:没有考虑括号两个括号相遇时要出栈
2.2.题目2:7-7 朋友圈

2.2.1设计思路
该题是应用并查集,每个俱乐部的成员和该俱乐部第一个成员合并,最后哈希得到最大的朋友圈人数,为了减少查找时间,尽力让节点指向根。
#include <iostream>
using namespace std;
int stu[30010]定义全局变量
int Find(int x)
{
if (如果x等于stu[x])说明根是自己
{
返回 stu[x];
}
else 继续递归找根
{
return stu[x]=Find(stu[x]);尽量让节点指向根
}
}
void add(int a, int b)将a和b合并
{
int x = Find(a);查找根
int y = Find(b);查找根
if (x != y)合并
{
stu[x] = y;
}
}
int main()
{
int N, M;
cin >> N >> M;
for (int i = 1; i <= N; i++) 并查集初始化,根是自己
{
stu[i] = i;
}
for (int i = 0; i < M; i++)
{
int count,a;
cin >> count >> a;
int b;
for (int j = 0; j < count - 1; j++)
{
cin >> b;
add(a, b);//调用合并函数
}
}
int max = 0;
int myhash[30010] = { 0 };hash求最大朋友圈人数
for (int i = 1; i <= N; i++)
{
int temp = Find(i);找根
myhash[temp]++;根一样加一
if (myhash[temp] > max)找最大值
{
max = myhash[temp];
}
}
cout << max;
return 0;
}
2.2.2代码截图


2.2.3本题PTA提交列表说明

Q: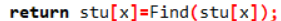 在递归时尽量让节点都指向根
在递归时尽量让节点都指向根
2.3.题目3:7-6 修理牧场

2.3.1设计思路
这个就是一个哈夫曼树,使用multiset(set不能存放多个相同数据),multiset是从小到大排序好的,每次取最小两个数据相加,然后作为新的元素加入multiset中(当然这两个得删除),直到只剩一个数据,用sum记录所有相加和,sum即为所求最小花费。
- 注意使用erase删除元素时要用指针,如果直接使用数据会把multiset中所有该数据删除,比如erase(3),将会删除所有的3
2.3.2代码截图

2.3.3本题PTA提交列表说明

A:此题难点不是在于代码,而是思路,当时刚好学完哈夫曼树,然后又有STL的加持,就会显得很轻松就过。
3.阅读代码
3.1 题目
题目描述
在桌面上有一排硬币,共NN枚,每一枚硬币均为正面朝上。现在要把所有的硬币翻转成反面朝上,规则是每次可翻转任意N-1N−1枚硬币(正面向上的被翻转为反面向上,反之亦然)。求一个最短的操作序列(将每次翻转N-1枚硬币成为一次操作)。
输入输出格式
输入格式:
一个自然数NN(NN为不大于100100的偶数)。
输出格式:
第一行包含一个整数SS,表示最少需要的操作次数。接下来的SS行每行分别表示每次操作后桌上硬币的状态(一行包含NN个整数(00或11),表示每个硬币的状态:00――正面向上,和11――反面向上,不允许出现多余空格)。
对于有多种操作方案的情况,则只需字典序最小输出一种。
输入输出样例
输入样例#1: 复制
4
输出样例#1: 复制
4
0111
1100
0001
1111
3.2 解题思路
翻n-1枚硬币,就是有一枚不翻,也可以理解为翻一枚
3.3 代码截图

3.4 学习体会
逻辑性的题目一般可以找出规律性,看上去可能很麻烦但是可以其实代码量很少,或者有时候可以巧妙地借助STL完成解题。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号