splay tree



类别：二叉排序树
空间效率：O(n)
时间效率：O(log n)内完成插入、查找、删除操作
创造者：Daniel Sleator和Robert Tarjan
优点：每次查询会调整树的结构，使被查询频率高的条目更靠近树根。

注：所有图片来自wiki。

Tree Rotation


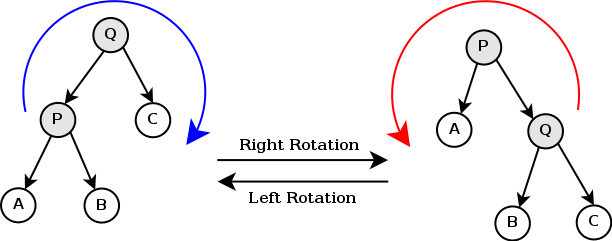
树的旋转是splay的基础，对于二叉查找树来说，树的旋转不破坏查找树的结构。

Splaying


Splaying是Splay Tree中的基本操作，为了让被查询的条目更接近树根，Splay Tree使用了树的旋转操作，同时保证二叉排序树的性质不变。
Splaying的操作受以下三种因素影响：
  • 节点x是父节点p的左孩子还是右孩子
  • 节点p是不是根节点，如果不是
  • 节点p是父节点g的左孩子还是右孩子
同时有三种基本操作：

Zig Step



当p为根节点时，进行zip step操作。
当x是p的左孩子时，对x右旋；
当x是p的右孩子时，对x左旋。

Zig-Zig Step



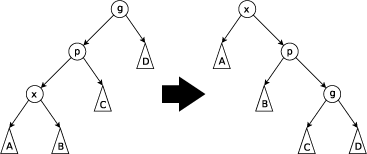
当p不是根节点，且x和p同为左孩子或右孩子时进行Zig-Zig操作。
当x和p同为左孩子时，依次将p和x右旋；
当x和p同为右孩子时，依次将p和x左旋。


Zig-Zag Step



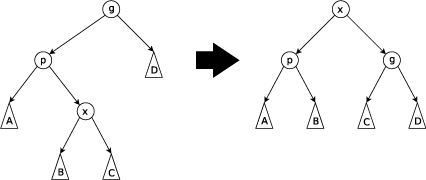
当p不是根节点，且x和p不同为左孩子或右孩子时，进行Zig-Zag操作。
当p为左孩子，x为右孩子时，将x左旋后再右旋。
当p为右孩子，x为左孩子时，将x右旋后再左旋。


应用


Splay Tree可以方便的解决一些区间问题，根据不同形状二叉树先序遍历结果不变的特性，可以将区间按顺序建二叉查找树。
每次自下而上的一套splay都可以将x移动到根节点的位置，利用这个特性，可以方便的利用Lazy的思想进行区间操作。
对于每个节点记录size，代表子树中节点的数目，这样就可以很方便地查找区间中的第k小或第k大元素。
对于一段要处理的区间[x, y]，首先splay x-1到root，再splay y+1到root的右孩子，这时root的右孩子的左孩子对应子树就是整个区间。
这样，大部分区间问题都可以很方便的解决，操作同样也适用于一个或多个条目的添加或删除，和区间的移动。

POJ2764 Feed the dogs

http://poj.org/problem?id=2764
http://blog.csdn.net/cyberzhg/article/details/8058154

区间不会重叠，所以不可能有首首相同或尾尾相同的情况，读入所有区间，按照右端由小到大排序。然后通过维护splay进行第k小元素的查询操作。
[cpp] view plaincopyprint?
 
 
  1. #include <cstdio>  
  2. #include <cstring>  
  3. #include <algorithm>  
  4. using namespace std;  
  5. const int MAXN = 100005;  
  6. const int MAXM = 50005;  
  7. const int INF = 0x7FFFFFFF;  
  8.   
  9. class SplayTree  
  10. {  
  11. public:  
  12.     SplayTree()  
  13.     {  
  14.         nil = &_nil;  
  15.         _nil.value = 0;  
  16.         _nil.size = 0;  
  17.         _nil.parent = nil;  
  18.         _nil.child[LEFT] = nil;  
  19.         _nil.child[RIGHT] = nil;  
  20.     }  
  21.   
  22.     inline void clear()  
  23.     {  
  24.         nodeNumber = 0;  
  25.         root = nil;  
  26.         insert(-INF);  
  27.         insert(INF);  
  28.     }  
  29.   
  30.     inline void insert(const int value)  
  31.     {  
  32.         if(root == nil)  
  33.         {  
  34.             root = newNode(nil, value);  
  35.             return;  
  36.         }  
  37.         Node *x = root;  
  38.         while(true)  
  39.         {  
  40.             int dir = x->value < value;  
  41.             if(x->child[dir] == nil)  
  42.             {  
  43.                 x->child[dir] = newNode(x, value);  
  44.                 update(x);  
  45.                 splay(x->child[dir], nil);  
  46.                 return;  
  47.             }  
  48.             else  
  49.             {  
  50.                 x = x->child[dir];  
  51.             }  
  52.         }  
  53.     }  
  54.   
  55.     inline void remove(const int value)  
  56.     {  
  57.         int k = find(value);  
  58.         find(k - 1, nil);  
  59.         find(k + 1, root);  
  60.         root->child[RIGHT]->child[LEFT] = nil;  
  61.         update(root->child[RIGHT]);  
  62.         update(root);  
  63.     }  
  64.   
  65.     inline int getKth(const int k)  
  66.     {  
  67.         find(k + 1, nil);  
  68.         return root->value;  
  69.     }  
  70.   
  71.     inline void print()  
  72.     {  
  73.         printf("Splay Tree: \n");  
  74.         print(root);  
  75.         printf("\n");  
  76.     }private:  
  77.     static const int LEFT = 0;  
  78.     static const int RIGHT = 1;  
  79.     struct Node  
  80.     {  
  81.         int value, size;  
  82.         Node *parent, *child[2];  
  83.     } _nil, node[MAXN];  
  84.     int nodeNumber;  
  85.     Node *root, *nil;  
  86.   
  87.     inline Node *newNode(Node *parent, const int value)  
  88.     {  
  89.         node[nodeNumber].value = value;  
  90.         node[nodeNumber].size = 1;  
  91.         node[nodeNumber].parent = parent;  
  92.         node[nodeNumber].child[LEFT] = nil;  
  93.         node[nodeNumber].child[RIGHT] = nil;  
  94.         return &node[nodeNumber++];  
  95.     }  
  96.   
  97.     inline void update(Node *x)  
  98.     {  
  99.         if(x == nil)  
  100.         {  
  101.             return;  
  102.         }  
  103.         x->size = x->child[LEFT]->size + x->child[RIGHT]->size + 1;  
  104.     }  
  105.   
  106.     inline void rotate(Node *x, const int dir)  
  107.     {  
  108.         Node *p = x->parent;  
  109.         p->child[!dir] = x->child[dir];  
  110.         p->child[!dir]->parent = p;  
  111.         x->child[dir] = p;  
  112.         x->parent = p->parent;  
  113.         if(p->parent->child[LEFT] == p)  
  114.         {  
  115.             p->parent->child[LEFT] = x;  
  116.         }  
  117.         else  
  118.         {  
  119.             p->parent->child[RIGHT] = x;  
  120.         }  
  121.         p->parent = x;  
  122.         update(p);  
  123.         update(x);  
  124.         if(root == p)  
  125.         {  
  126.             root = x;  
  127.         }  
  128.     }  
  129.   
  130.     inline void splay(Node *x, Node *y)  
  131.     {  
  132.         while(x->parent != y)  
  133.         {  
  134.             if(x->parent->parent == y)  
  135.             {  
  136.                 if(x->parent->child[LEFT] == x)  
  137.                 {  
  138.                     rotate(x, RIGHT);  
  139.                 }  
  140.                 else  
  141.                 {  
  142.                     rotate(x, LEFT);  
  143.                 }  
  144.             }  
  145.             else if(x->parent->parent->child[LEFT] == x->parent)  
  146.             {  
  147.                 if(x->parent->child[LEFT] == x)  
  148.                 {  
  149.                     rotate(x->parent, RIGHT);  
  150.                     rotate(x, RIGHT);  
  151.                 }  
  152.                 else  
  153.                 {  
  154.                     rotate(x, LEFT);  
  155.                     rotate(x, RIGHT);  
  156.                 }  
  157.             }  
  158.             else  
  159.             {  
  160.                 if(x->parent->child[RIGHT] == x)  
  161.                 {  
  162.                     rotate(x->parent, LEFT);  
  163.                     rotate(x, LEFT);  
  164.                 }  
  165.                 else  
  166.                 {  
  167.                     rotate(x, RIGHT);  
  168.                     rotate(x, LEFT);  
  169.                 }  
  170.             }  
  171.             update(x);  
  172.         }  
  173.     }  
  174.   
  175.     inline void find(int k, Node *y)  
  176.     {  
  177.         Node *x = root;  
  178.         while(k != x->child[LEFT]->size + 1)  
  179.         {  
  180.             if(k <= x->child[LEFT]->size)  
  181.             {  
  182.                 x = x->child[LEFT];  
  183.             }  
  184.             else  
  185.             {  
  186.                 k -= x->child[LEFT]->size + 1;  
  187.                 x = x->child[RIGHT];  
  188.             }  
  189.         }  
  190.         splay(x, y);  
  191.     }  
  192.   
  193.     inline int find(const int value)  
  194.     {  
  195.         Node *x = root;  
  196.         int count = 0;  
  197.         while(true)  
  198.         {  
  199.             if(x->value == value)  
  200.             {  
  201.                 return count + x->size - x->child[RIGHT]->size;  
  202.             }  
  203.             else if(x->value > value)  
  204.             {  
  205.                 x = x->child[LEFT];  
  206.             }  
  207.             else  
  208.             {  
  209.                 count += x->size - x->child[RIGHT]->size;  
  210.                 x = x->child[RIGHT];  
  211.             }  
  212.         }  
  213.     }  
  214.   
  215.     inline void print(Node *x)  
  216.     {  
  217.         if(x == nil)  
  218.         {  
  219.             return;  
  220.         }  
  221.         printf("%d: %d %d %d\n", x->value, x->child[LEFT]->value, x->child[RIGHT]->value, x->size);  
  222.         print(x->child[LEFT]);  
  223.         print(x->child[RIGHT]);  
  224.     }  
  225. } splay;  
  226.   
  227. struct Interval  
  228. {  
  229.     int a, b, k, index;  
  230.     bool operator < (const Interval &interval) const  
  231.     {  
  232.         return b < interval.b;  
  233.     }  
  234. } interval[MAXM];int pretty[MAXN];int ans[MAXM];  
  235.   
  236. int main()  
  237. {  
  238.     int n, m;  
  239.     while(~scanf("%d%d", &n, &m))  
  240.     {  
  241.         for(int i=1;i<=n;++i)  
  242.         {  
  243.             scanf("%d", &pretty[i]);  
  244.         }  
  245.         for(int i=0;i<m;++i)  
  246.         {  
  247.             scanf("%d%d%d", &interval[i].a, &interval[i].b, &interval[i].k);  
  248.             interval[i].index = i;  
  249.         }  
  250.         sort(interval, interval + m);  
  251.         splay.clear();  
  252.         int a = 1, b = 0;  
  253.         for(int i=0;i<m;++i)  
  254.         {  
  255.             for(int j=a;j<interval[i].a && j<=b;++j)  
  256.             {  
  257.                 splay.remove(pretty[j]);  
  258.             }  
  259.             for(int j=max(interval[i].a, b+1);j<=interval[i].b;++j)  
  260.             {  
  261.                 splay.insert(pretty[j]);  
  262.             }  
  263.             a = interval[i].a;  
  264.             b = interval[i].b;  
  265.             ans[interval[i].index] = splay.getKth(interval[i].k);  
  266.         }  
  267.         for(int i=0;i<m;++i)  
  268.         {  
  269.             printf("%d\n", ans[i]);  
  270.         }  
  271.     }  
  272.     return 0;  
  273. }  

POJ3580 SuperMemo

http://poj.org/problem?id=3580
http://blog.csdn.net/cyberzhg/article/details/8053293

在序列首尾加上值为INF的点。一共六种操作：
1. ADD x y D
将x到y区间加上D。
利用lazy。将x-1位置splay到root，y+1位置splay到root的右孩子，这时y+1位置的左孩子就是区间的范围。
2. REVERSE x y 反转x到y区间
和ADD类似，记录区间是否反转，在需要的时候调换左右孩子。
3. REVOLVE x y T 将x到y区间循环右移T次
DELETE和INSERT的综合，两次区间操作。
4. INSERT x P 在x位置后插入P
和ADD类似，将区间设为空，插入新的数值。
5. DELETE x 删除x位置的数
和ADD类似，将最终区间设为空。
6. MIN x y 求x到y区间中的最小值
和ADD类似，记录所有子树的min，在旋转的过程中更新。

[cpp] view plaincopyprint?
 
 
  1. #include <cstdio>  
  2. #include <cstring>  
  3. #include <algorithm>  
  4. using namespace std;  
  5. const int MAXN = 100005;  
  6. const int MAXM = 100005;  
  7. const int INF = 0x7fffffff;  
  8.   
  9. class SplayTree  
  10. {  
  11. public:  
  12.     SplayTree()  
  13.     {  
  14.         nil.size = 0;  
  15.         nil.value = INF;  
  16.         nil.min = INF;  
  17.         nil.lchild = &nil;  
  18.         nil.rchild = &nil;  
  19.         nil.parent = &nil;  
  20.     }  
  21.   
  22.     inline void make(int array[], int n)  
  23.     {  
  24.         nodeNumber = 0;  
  25.         int mid = (n - 1) >> 1;  
  26.         root = newNode(&nil, array[mid]);  
  27.         root->lchild = make(0, mid - 1, root, array);  
  28.         root->rchild = make(mid + 1, n - 1, root, array);  
  29.         update(root);  
  30.     }  
  31.   
  32.     inline void ADD(int x, int y, int D)  
  33.     {  
  34.         find(x, &nil);  
  35.         find(y + 2, root);  
  36.         root->rchild->lchild->lazy += D;  
  37.     }  
  38.   
  39.     inline void REVERSE(int x, int y)  
  40.     {  
  41.         find(x, &nil);  
  42.         find(y + 2, root);  
  43.         root->rchild->lchild->isReverse ^= true;  
  44.     }  
  45.   
  46.     inline void REVOLVE(int x, int y, int T)  
  47.     {  
  48.         int len = y - x + 1;  
  49.         T = ((T % len) + len) % len;  
  50.         if(T)  
  51.         {  
  52.             find(y - T + 1, &nil);  
  53.             find(y + 2, root);  
  54.             SplayNode *d = root->rchild->lchild;  
  55.             root->rchild->lchild = &nil;  
  56.             find(x, &nil);  
  57.             find(x + 1, root);  
  58.             root->rchild->lchild = d;  
  59.             d->parent = root->rchild;  
  60.         }  
  61.     }  
  62.   
  63.     inline void INSERT(int x, int P)  
  64.     {  
  65.         find(x + 1, &nil);  
  66.         find(x + 2, root);  
  67.         root->rchild->lchild = newNode(root->rchild, P);  
  68.     }  
  69.   
  70.     inline void DELETE(int x)  
  71.     {  
  72.         find(x, &nil);  
  73.         find(x + 2, root);  
  74.         root->rchild->lchild = &nil;  
  75.     }  
  76.   
  77.     inline void MIN(int x, int y)  
  78.     {  
  79.         find(x, &nil);  
  80.         find(y + 2, root);  
  81.         pushdown(root->rchild->lchild);  
  82.         printf("%d\n", root->rchild->lchild->min);  
  83.     }  
  84.   
  85.     inline void print()  
  86.     {  
  87.         printf("Splay Linear: \n");  
  88.         print(root);  
  89.         printf("\n");  
  90.     }  
  91.   
  92.     inline void prints()  
  93.     {  
  94.         printf("Splay Structure: \n");  
  95.         prints(root);  
  96.         printf("\n");  
  97.     }  
  98.   
  99. private:  
  100.     struct SplayNode  
  101.     {  
  102.         int value, size, lazy;  
  103.         SplayNode *parent, *lchild, *rchild;  
  104.         int min;  
  105.         bool isReverse;  
  106.     } nil, node[MAXN + MAXM];  
  107.     int nodeNumber;  
  108.     SplayNode *root;  
  109.   
  110.     inline SplayNode *newNode(SplayNode *parent, const int value)  
  111.     {  
  112.         node[nodeNumber].value = value;  
  113.         node[nodeNumber].size = 1;  
  114.         node[nodeNumber].lazy = 0;  
  115.         node[nodeNumber].parent = parent;  
  116.         node[nodeNumber].lchild = &nil;  
  117.         node[nodeNumber].rchild = &nil;  
  118.         node[nodeNumber].min = value;  
  119.         node[nodeNumber].isReverse = false;  
  120.         return &node[nodeNumber++];  
  121.     }  
  122.   
  123.     SplayNode *make(int l, int r, SplayNode *parent, int array[])  
  124.     {  
  125.         if(l > r)  
  126.         {  
  127.             return &nil;  
  128.         }  
  129.         int mid = (l + r) >> 1;  
  130.         SplayNode *x = newNode(parent, array[mid]);  
  131.         x->lchild = make(l, mid - 1, x, array);  
  132.         x->rchild = make(mid + 1, r, x, array);  
  133.         update(x);  
  134.         return x;  
  135.     }  
  136.   
  137.     inline void update(SplayNode *x)  
  138.     {  
  139.         if(x == &nil)  
  140.         {  
  141.             return;  
  142.         }  
  143.         x->size = x->lchild->size + x->rchild->size + 1;  
  144.         x->min = min(x->value, min(x->lchild->min, x->rchild->min));  
  145.     }  
  146.   
  147.     inline void pushdown(SplayNode *x)  
  148.     {  
  149.         if(x == &nil)  
  150.         {  
  151.             return;  
  152.         }  
  153.         if(x->isReverse)  
  154.         {  
  155.             swap(x->lchild, x->rchild);  
  156.             x->lchild->isReverse ^= true;  
  157.             x->rchild->isReverse ^= true;  
  158.             x->isReverse = false;  
  159.         }  
  160.         if(x->lazy)  
  161.         {  
  162.             x->value += x->lazy;  
  163.             x->min += x->lazy;  
  164.             x->lchild->lazy += x->lazy;  
  165.             x->rchild->lazy += x->lazy;  
  166.             x->lazy = 0;  
  167.         }  
  168.     }  
  169.   
  170.     inline void rotateLeft(SplayNode *x)  
  171.     {  
  172.         SplayNode *p = x->parent;  
  173.         pushdown(x->lchild);  
  174.         pushdown(x->rchild);  
  175.         pushdown(p->lchild);  
  176.         p->rchild = x->lchild;  
  177.         p->rchild->parent = p;  
  178.         x->lchild = p;  
  179.         x->parent = p->parent;  
  180.         if(p->parent->lchild == p)  
  181.         {  
  182.             p->parent->lchild = x;  
  183.         }  
  184.         else  
  185.         {  
  186.             p->parent->rchild = x;  
  187.         }  
  188.         p->parent = x;  
  189.         update(p);  
  190.         update(x);  
  191.         if(root == p)  
  192.         {  
  193.             root = x;  
  194.         }  
  195.     }  
  196.   
  197.     inline void rotateRight(SplayNode *x)  
  198.     {  
  199.         SplayNode *p = x->parent;  
  200.         pushdown(x->lchild);  
  201.         pushdown(x->rchild);  
  202.         pushdown(p->rchild);  
  203.         p->lchild = x->rchild;  
  204.         p->lchild->parent = p;  
  205.         x->rchild = p;  
  206.         x->parent = p->parent;  
  207.         if(p->parent->lchild == p)  
  208.         {  
  209.             p->parent->lchild = x;  
  210.         }  
  211.         else  
  212.         {  
  213.             p->parent->rchild = x;  
  214.         }  
  215.         p->parent = x;  
  216.         update(p);  
  217.         update(x);  
  218.         if(root == p)  
  219.         {  
  220.             root = x;  
  221.         }  
  222.     }  
  223.   
  224.     inline void splay(SplayNode *x, SplayNode *y)  
  225.     {  
  226.         pushdown(x);  
  227.         while(x->parent != y)  
  228.         {  
  229.             if(x->parent->parent == y)  
  230.             {  
  231.                 if(x->parent->lchild == x)  
  232.                 {  
  233.                     rotateRight(x);  
  234.                 }  
  235.                 else  
  236.                 {  
  237.                     rotateLeft(x);  
  238.                 }  
  239.             }  
  240.             else if(x->parent->parent->lchild == x->parent)  
  241.             {  
  242.                 if(x->parent->lchild == x)  
  243.                 {  
  244.                     rotateRight(x->parent);  
  245.                     rotateRight(x);  
  246.                 }  
  247.                 else  
  248.                 {  
  249.                     rotateLeft(x);  
  250.                     rotateRight(x);  
  251.                 }  
  252.             }  
  253.             else  
  254.             {  
  255.                 if(x->parent->rchild == x)  
  256.                 {  
  257.                     rotateLeft(x->parent);  
  258.                     rotateLeft(x);  
  259.                 }  
  260.                 else  
  261.                 {  
  262.                     rotateRight(x);  
  263.                     rotateLeft(x);  
  264.                 }  
  265.             }  
  266.         }  
  267.         update(x);  
  268.     }  
  269.   
  270.     inline void find(int k, SplayNode *y)  
  271.     {  
  272.         SplayNode *x = root;  
  273.         pushdown(x);  
  274.         while(k != x->lchild->size + 1)  
  275.         {  
  276.             if(k <= x->lchild->size)  
  277.             {  
  278.                 x = x->lchild;  
  279.             }  
  280.             else  
  281.             {  
  282.                 k -= x->lchild->size + 1;  
  283.                 x = x->rchild;  
  284.             }  
  285.             pushdown(x);  
  286.         }  
  287.         splay(x, y);  
  288.     }  
  289.   
  290.     inline void print(SplayNode *x)  
  291.     {  
  292.         if(x == &nil)  
  293.         {  
  294.             return;  
  295.         }  
  296.         pushdown(x);  
  297.         print(x->lchild);  
  298.         printf("%d: %d %d %d %d\n", x->value, x->min, x->parent->value, x->lchild->value, x->rchild->value);  
  299.         print(x->rchild);  
  300.     }  
  301.   
  302.     inline void prints(SplayNode *x)  
  303.     {  
  304.         if(x == &nil)  
  305.         {  
  306.             return;  
  307.         }  
  308.         pushdown(x);  
  309.         if(x->value == INF)  
  310.         {  
  311.             printf("INF : ");  
  312.         }  
  313.         else  
  314.         {  
  315.             printf("%d : ", x->value);  
  316.         }  
  317.         if(x->lchild == &nil)  
  318.         {  
  319.             printf("nil ");  
  320.         }  
  321.         else  
  322.         {  
  323.             if(x->lchild->value == INF)  
  324.             {  
  325.                 printf("INF ");  
  326.             }  
  327.             else  
  328.             {  
  329.                 printf("%d ", x->lchild->value);  
  330.             }  
  331.         }  
  332.         if(x->rchild == &nil)  
  333.         {  
  334.             printf("nil\n");  
  335.         }  
  336.         else  
  337.         {  
  338.             if(x->rchild->value == INF)  
  339.             {  
  340.                 printf("INF\n");  
  341.             }  
  342.             else  
  343.             {  
  344.                 printf("%d\n", x->rchild->value);  
  345.             }  
  346.         }  
  347.         prints(x->lchild);  
  348.         prints(x->rchild);  
  349.     }  
  350. } splayTree;  
  351.   
  352. char buffer[128];int array[MAXN];int n, m;  
  353.   
  354. int main()  
  355. {  
  356.     int x, y, D, T, P;  
  357.     scanf("%d", &n);  
  358.     for(int i=1;i<=n;++i)  
  359.     {  
  360.         scanf("%d", &array[i]);  
  361.     }  
  362.     array[0] = INF;  
  363.     array[n+1] = INF;  
  364.     splayTree.make(array, n + 2);  
  365.     scanf("%d", &m);  
  366.     while(m--)  
  367.     {  
  368.         scanf("%s", buffer);  
  369.         switch(buffer[0])  
  370.         {  
  371.         case 'A':  
  372.             scanf("%d%d%d", &x, &y, &D);  
  373.             splayTree.ADD(x, y, D);  
  374.             break;  
  375.         case 'R':  
  376.             if('E' == buffer[3])  
  377.             {  
  378.                 scanf("%d%d", &x, &y);  
  379.                 splayTree.REVERSE(x, y);  
  380.             }  
  381.             else  
  382.             {  
  383.                 scanf("%d%d%d", &x, &y, &T);  
  384.                 splayTree.REVOLVE(x, y, T);  
  385.             }  
  386.             break;  
  387.         case 'I':  
  388.             scanf("%d%d", &x, &P);  
  389.             splayTree.INSERT(x, P);  
  390.             break;  
  391.         case 'D':  
  392.             scanf("%d", &x);  
  393.             splayTree.DELETE(x);  
  394.             break;  
  395.         case 'M':  
  396.             scanf("%d%d", &x, &y);  
  397.             splayTree.MIN(x, y);  
  398.             break;  
  399.         }  
  400.     }  
  401.     return 0;  
  402. }  
posted @ 2017-07-19 17:28  Code-dream  阅读(310)  评论(0)  编辑  收藏  举报