排序之堆排序

堆是一种根节点和孩子结点具有某种关系的二叉树，具体可以分为大顶堆和小顶堆，其中大顶堆中的所有父结点的值比它的孩子结点的值要大，而左右孩子的值不做对比；反之就是小顶堆。

堆排序是根据堆的性质，进行反复的位置调换和堆调整的过程，要进行堆排序，首先就需要创建堆，这里选择创建大顶堆，创建大顶堆涉及到位置调整，假设对堆中位置为 i 的结点进行位置调整，调整算法为下：

max_heapify(A,i)

1、l =left(i);// i结点的左孩子

2、r=right(i);

3、if l<=heap_size(A) and A[l]>A[i]

4、　　then largest=l;

5、　　else larges=i;

6、if r<=heap_size(A) and A[r]>A[largest]

7、　　then largest=r;

8、if largest != i

9、　　then exchange(A[i],A[largest]);

10、　　max_heapify(A,largest);//对array[largest]结点继续调整

创建堆的过程就是对结点进行持续调整位置的过程，创建堆的算法描述为：

build_max_heap(A)

1、heap_size(A)=length[A]

2、for i=length[A]/2 downto 1

3、　　do max_heapify(A,i);//对结点 i 进行位置调整

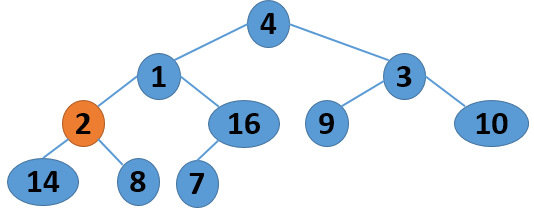
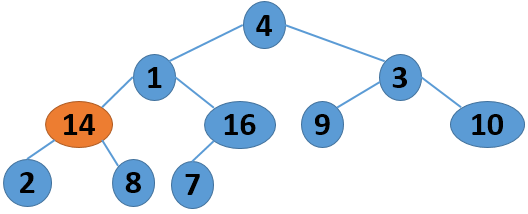
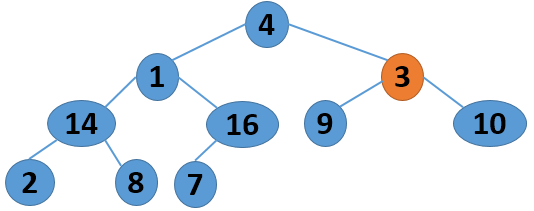
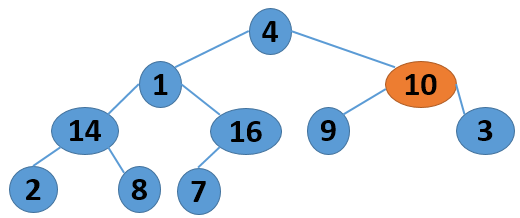
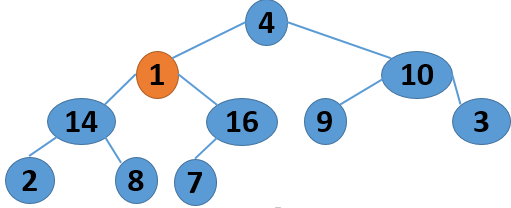
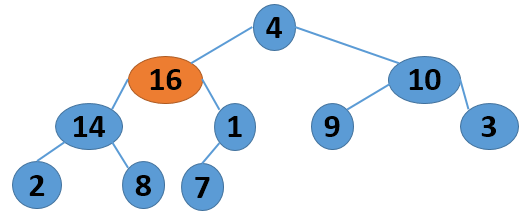
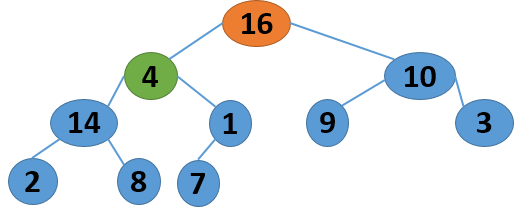
这里给出一个序列 4 1 3 2 16 9 10 14 8 7,取自《算法导论》中的内容，现给出其建堆的过程图：

 

 

 

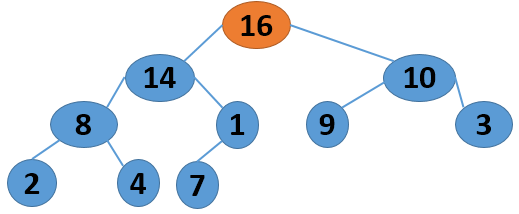
注意，以上的调整过程，是从左到右、从上到下进行调整的过程。堆建好了，怎么进行排序呢？答案还是进行数的位置调整，我们可以将堆顶的数据和最后一个叶子结点进行位置调换，然后对子序列Array[0,length-2]进行堆调整；继续将堆顶的数据和倒数第二个结点进行位置调换，然后对子序列Array[0,length-3]进行堆调整....,算法描述如下：

heap_sort(A)

1、build_max_heap(A)

2、for i=length(A) down to 2

3、　　do exchange( A[1], A[i])//堆顶值和A[i]进行位置调换

4、　　heap_size(A)=heap_size(A)-1

5、　　max_heapify(A,1)//进行顶点位置的调整

根据算法描述，可以得出程序结果，设计如下：

public class my{
    public static void main(String[] args)throws InterruptedException{
        int arr[]={1,4,23,0,4,5,34,23,4354,23,12};
        printArray(arr);
        heap_sort(arr);
        printArray(arr);
    
    }
    //进行堆排序
    static void heap_sort(int[] array){
        build_max_heap(array);//创建最大堆
        int length=array.length;
        int temp=0;
        for(int i=array.length-1;i>=0;i--){
            temp=array[i];//堆的第一个元素最大，将第一个元素移动到最后，然后对第一个元素进行位置调整
            array[i]=array[0];
            array[0]=temp;
            length--;//由于位置为length及其以后的元素已经排好序了，堆的调整范围是从0到length-1
            max_heapfy(array,0,length);
        }
    }
    //创建最大堆
    static void build_max_heap(int[] array){
        //创建最大堆时，为什么下标从array.length/2开始？因为这样可以将最大的值推到堆顶位置，从以上
        //具体图示位置的调换过程可知，需要从array.length/2开始进行调整。
        for(int i=array.length/2;i>=0;i--){
            max_heapfy(array,i,array.length);
        }
    }
    static void max_heapfy(int[] array,int i,int arraysize){
        int leftchild=i*2+1,rightchild=i*2+2;
        int largest=i,temp=0;
        //以下两个判断是寻找array[i]以及它的左右孩子中值最大的下标
        if(leftchild<arraysize && array[leftchild]>array[i]){
            largest=leftchild;
        }
        if(rightchild<arraysize && array[rightchild]>array[largest]){
            largest=rightchild;
        }
        //最大值的下表如果不是i的话，就进行位置的变动，将array[i]和
        //array[largest]进行位置置换，然后再对位置largest进行max_heapfy调整
        if(largest!=i){
            temp=array[largest];
            array[largest]=array[i];
            array[i]=temp;
            max_heapfy(array,largest,arraysize);
        }
    }    
    static void printArray(int[] array){
        for(int val:array){
            System.out.print(val+" ");
        }
        System.out.println();
    }
}

最后的输出：

1 4 23 0 4 5 34 23 4354 23 12
0 1 4 4 5 12 23 23 23 34 4354

算法分析：

堆排序的时间复杂度是O(nlgn)（最坏的情况下也是如此），空间复杂度是O(1)，与归并排序相比，堆排序的空间节省要多很多。