贪心算法(greedy algorithm):贪心算法的思想很简单，求解一个问题分为多个步骤，每次求解时总是做出在当前步骤来看是最优的解，在求解问题时，往往需要对给定的集合中的数据进行一次遍历，有时候一次遍历还可能找不出所需要的答案，这时候就需要进行多次遍历，每一次遍历其实就是一步求解，就是对下一个子问题的解答，利用贪心算法解决问题不总是那么容易，因为你不总能一下子就能对问题的解决方案进行贪心描述的，也就是贪心策略的构建不总是那么容易被识别，贪心算法求解问题也有一些思路：
a 将原问题分解为子问题，原问题是一个总的描述，它寻求是一个整的结果，子问题可以理解为求解原问题的一些步骤，比如说第一步该怎么做，第一步做完了下一步又该怎么做
b 找出贪心策略，策略就是“该怎么做”，确定了“该怎么做”也就确定了策略
c 根据贪心策略求解每一个子问题的最优解
d 合并所有局部最优解，作为原问题的解返还给调用方
贪心算法是有局限性的，它得出的解可能是该问题的一个合适的解，但可能不是“最优解”，它的特点有：
a 所求解只是一个合适的解
b 不能用该策略求解最优解，“最值”问题不能使用该策略
用示例来理解贪心算法，例如：
1、排班问题，有几个活动公用一间教室，该教室每次只允许一个活动上演，请给出一个排班计划，要求尽可能多地安排活动，例如这些活动的安排时间有：
a(1,3) b(2,3) c(4,6) e(4,5) f(5,6),a活动开始时间是1点，结束时间是3点，b活动开始时间是2点，结束时间是3点，排班思路：
- 将活动的结束时间从小到大进行排列
- 选定排好序的第一个活动为初始活动，寻找下一个活动，条件是下一个活动的开始时间要大于该活动的结束时间
- 用相同的策略执行步骤2
def arrangeActivity(activitiesList):
//根据结束时间从小到大对活动进行排序
sortActivities(activitiesList);
//选定第一个活动作为初始活动
initialActivity=activitiesList[0];
result.add(activitiesList[0]);
for i=1 to activitiesList.length:
if initialActivity.endTime < activitiesList[i].startTime:
//将下一个活动做为初始活动
initialActivity=activitiesList[i];
result.add(activitiesList[i]);
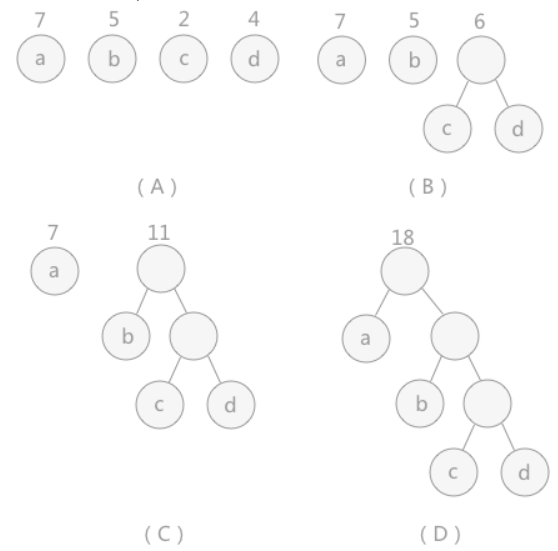
2、哈夫曼树的构建：哈夫曼树也是利用贪心算法进行构建的，给定一组带有权重的节点，将这些节点构建成一棵树，但是是有条件的，每次构建的时候需要将权重最小的两个节点作为叶子节点，其父节点的权重变为两个叶子节点的权重和，然后将合并后的父节点放到原来的节点集合中，继续构建新的树，已经用过的节点不能再次使用
def constructHuffmanTree(nodeSet):
while(nodeSet.size()>1):
//根据权重从小到大对节点值进行排序
sortNodeSetByWeight(nodeSet);
//获取权重最小的两个节点
node1=nodeSet.remove(0);
node2=nodeSet.remove(0);
//合并两个节点的权重作为父节点的权重
newNode=new Node(node1.weight+node2.weight);
//注意创建叶子节点
newNode.left=node1;
newNode.right=node2;
//将新的节点放到节点集合中
nodeSet.add(newNode);
//当节点集中只剩一个节点时，该节点就是最终的结果
return nodeSet.get(0);
哈夫曼树的构建过程也是贪心算法的一种体现，每次只选取权重值最小的两个节点进行构建，同时将这两个权重值最小的节点从原节点集中进行删除，按照这种策略继续进行构建，直到节点集合中只剩下最后一个节点。
总结，使用贪心算法进行问题求解时，总的解题步骤有：
1、扫描原数据集，找出符合要求的数据
2、根据符合要求的数据来构建局部最优解，然后继续进行1，2步骤，直到求出所有子问题的解
