一、行列式
概念
行列式是行数和列数相等的数字阵列,本质是一个数。
n阶行列式
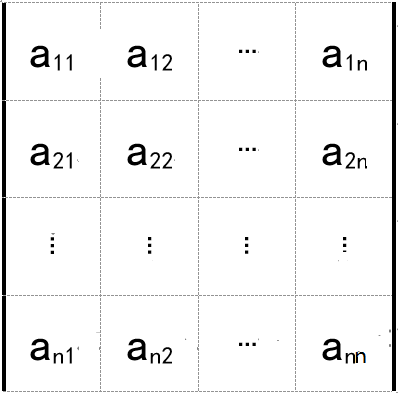
&完全展开式
是所有取自n阶行列式不同行不同列的n个元素的乘积之和
逆序数
从左到右依次选定数,选定数后面的一个数比选定数小则算作一个逆序,一个排列的逆序总数称为逆序数
偶排列
逆序数为偶数的排列
行列式性质
- 行列式运算性质
- 行列式转置,行列式值不变
- 两行(或列)互换位置,行列式值变号
- 某行(或列)有公因子k,可把k提出行列式记号外
- 如果行列式某行(或列)是两个元素之和,则可把行列式拆成两个行列式之和
- 把某行(或列)的k倍加到另一行(或列),行列式值不变
- 行列式等0性质
- 两行(或列)相同
- 某一行(或列)元素全为0
- 两行(或列)元素对应成比例
行列式按行展开
n阶行列式的值等于任意一行(列)元素与其对应代数余子式乘积之和
异乘变零定理
行列式的任一行(列)元素与令一行(列)元素的代数余子式的乘积之和为0
余子式
选定某一元素aij,划去该元素所在的行和列,余下的部分相对位置不变,组成的行列式称为余子式。记作Mij
代数余子式
余子式乘上(-1)的i+j次方得到aij的代数余子式,记作Aij
行列式求值
上(下)三角行列式
主对角线元素的乘积
上(下)倒三角行列式
(-1)的n(n-1)/2次方 乘 副对角线元素乘积(n为行列式阶数)
&拉普拉斯展开定理
选定k行,选定k列组成的k阶子式 与 余子式(除去所在行、所在列剩下相对位置不变的行列式) 相乘,乘以(-1)的 选定k阶子式所在行、所在列的行标和列标之和次方
&两个特殊的拉普拉斯展开式
|A *| |A 0|
= =|A|乘|B|,
|0 B| |* B|
|* A| |0 A|
= =|A|乘|B|乘(-1)的m乘n次方(A为m阶、B为n阶行列式)
|B 0| |B *|
范德蒙德行列式公式
|1 1 ... 1|
|x1 x2 ... xn|
|x1^2 x2^2 ... xn^2| = TT(xi - xj)
|... ... ... ...|
|x1^n-1 x2^n-1 ... x3^n-1|
例:
令xj = 2;xi = -1,3;令xj = -1;xi = 3
|1 1 1|
|2 -1 3| = (-1-2)(3-2)(3-(-1))
|.. .. ..|
&克莱姆法则
适用于n个方程,n个未知量的方程组,|A|为系数行列式
推论
-
对于非齐次方程组:
- 系数行列式|A| != 0
- xi = |Ai|/|A|(i=1,2,..n),|Ai|是第i列元素替换成方程组右端常数项构成的行列式
- 系数行列式|A| != 0,则方程组有唯一解
-
对于齐次方程组:
- 系数行列式|A| != 0的充要条件是 方程组有唯一零解。若有非零解,充要条件是系数行列式|A|=0


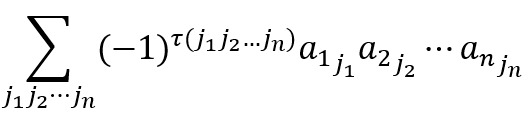

 浙公网安备 33010602011771号
浙公网安备 33010602011771号