数制介绍和转换
概述
我们平常最习惯的是十进制数，而计算机硬件内部唯一能识别的是二进制数，任何其他计数值和信息在计算机内都要转化为二进制数。
十进制(decimal)
- 逢十进位
- 共有0 ~ 9十个数字符号，用D表示或不带任何标识默认为十进制数。例：20D或20
二进制(binary)
- 逢二进位
- 共有0，1两个数字符号，用B表示。例：1010B
介绍完最基本的两种数值，接下来我们介绍一种用于简化二进制表示的两种进制：
十六进制(Hex)
- 共有0 ~ 9,A ~ F 十六个数字符号
- 逢十六进位，用H表示。例：A3H
八进制(octal)
- 共有0 ~ 7八个数字符号
- 逢八进位，用O表示，例：20.52O
非十进制数向十进制数转换
使用按权展开公式完成非十进制数向十进制数转换
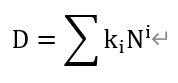
其中N为计数的基数，又称进位数；Ki为第i位的系数；Ni称为第i位的权；
备注：
- 小数点左起第一位的权位是0，左起第二位的权位是1，依次类推。
- 小数点右起第一位的权位是-1，右起第二位的权位是-2，依次类推。
下面展示使用该公式完成非十进制数向十进制数转换：
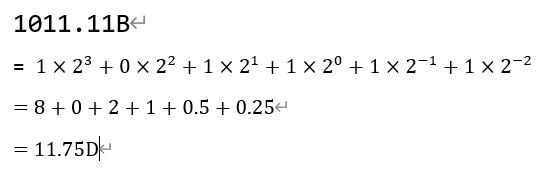
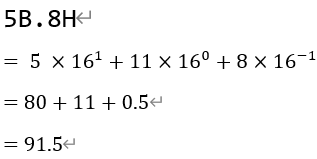
十进制到非十进制转换
对整数和小数两部分分别运算，最后组合即为答案。
- 十进制对N进制的转换:
- 对整数：除N取余，直到商为0为止。余数自下而上排列。
- 对小数：乘N取整。直到小数为0为止。整数自上而下排列。
下面展示十进制转换为非十进制的例子：
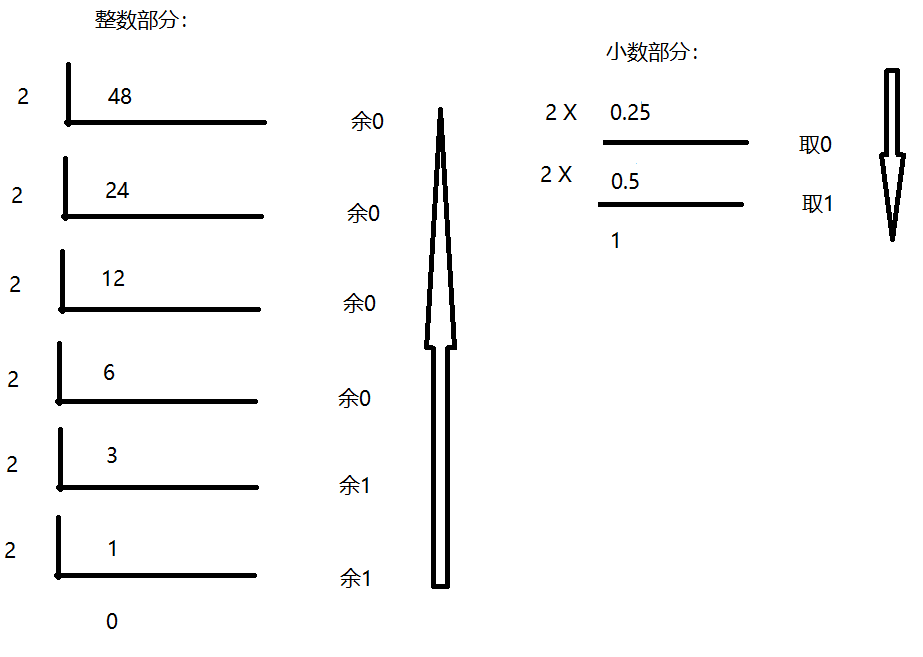
二进制数向非十进制数的转换
二进制数转换为十六(2的N次)方进制数
- 用4(N)位二进制数表示1位16(2的N次)进制数。
- 整数部分，从小数点左起第一位开始分组，每4(N)位一组，不够4(N)位高位补0。
- 小数部分，从小数点右起第一位开始分组，每4(N)位一组，不够4(N)位低位补0。
下面展示二进制数向非十进制数的转换的例子：
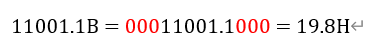
其中红色数字位补0部分。每4位一组，利用"8421法则"将得到的4个数值相加的和，与其他组得到的和拼接，即为转化后的十六进制数。
二进制数转换八进制数同理，但八进制使用的是"421法则"。
十六进制数转二进制数
1位十六进制数通过对应一组4位二进制数，这一组4位二进制数通过“8421法则”求和等于这一位十六进制数，再将得到的多个组拼接。
下面展示十六进制数向二进制数的转换的例子
（数电p8）
八进制数转二进制数
1位八进制数通过对应一组3位二进制数，这一组3位二进制数通过“421法则”求和等于这一位八进制数，再将得到的多个组拼接。
下面展示十六进制数向二进制数的转换的例子
（数电p9）
