神经网络(未完)
神经网络
perceptron(了解)
perceptron:最简单的ANN结构,它是一个linear threshold unit(LTU),接收wx,经过step func f,转为输出。step func通常是heaviside(返回0或1)或者sign(返回-1、0或1)
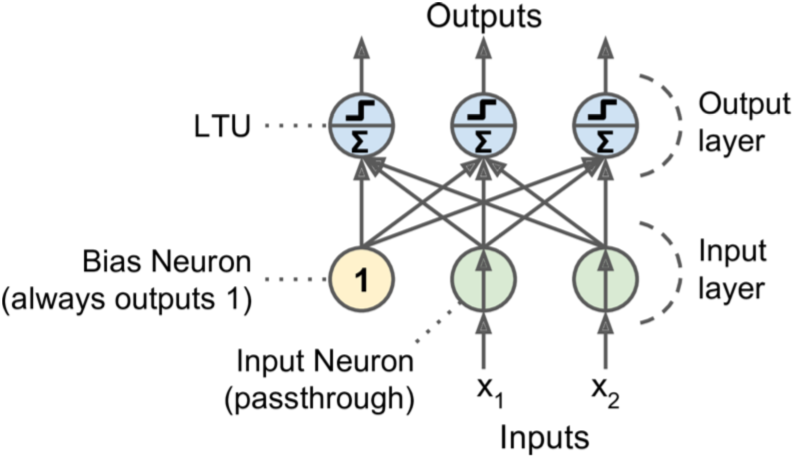
训练实际上就是更新w。过程是不断输入inputs,每个inputs都会得出一个output,当预测错误时,增强对正确判断贡献大的连接,即权重w。
\(w_{i,j} =w_{i,j}+η(\hat{y}_j−y_j)x_i\)
上述简单结构只适用于线性可分数据,几乎就是Stochastic Gradient Descent求解的无regularization的线性回归,所以效果并不好。
Multi-Layer Perceptron(MLP)
one (passthrough,即不作任何变化) input layer, one or more layers of LTUs, called hidden layers, and one final layer of LTUs called the output layer。
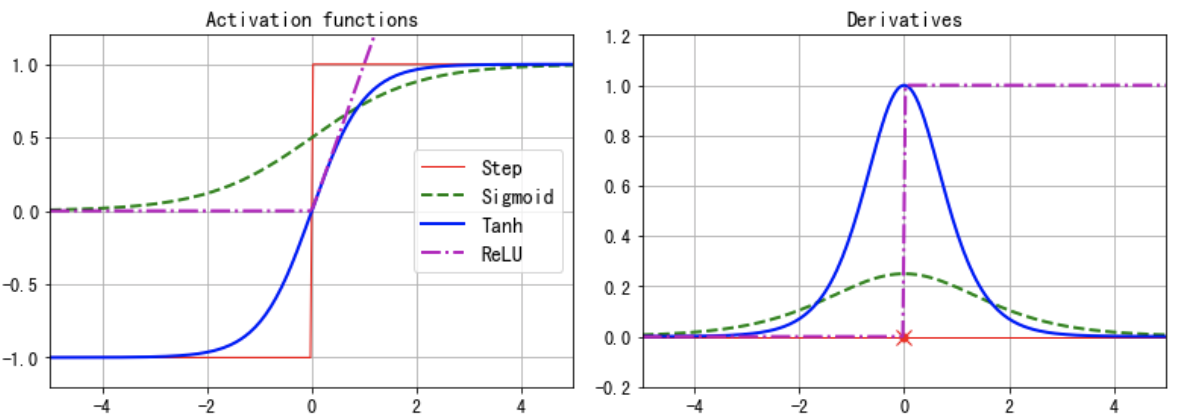
激活函数step func被sigmoid func取代,因为sigmoid的导数非0且到处可导,可以实现Back Propagation。其他激活函数有:
hyperbolic tangent function:$ tanh (z) = 2σ(2z) – 1$,它与sigmoid类似,但范围是-1到1,可以使得每层输出在训练开始时是normalized的(以0为中心),且通常加快收敛。
ReLU function:\(\max(0,z)\),它是连续的,但在z=0处不可导(the slope changes abruptly, which can make Gradient Descent bounce around)。但在实践上能够加快计算,更重要的是他的输出不会是最大值?可以减少GD期间的一些问题。
有多两层或以上的hidden layers称为DNN。
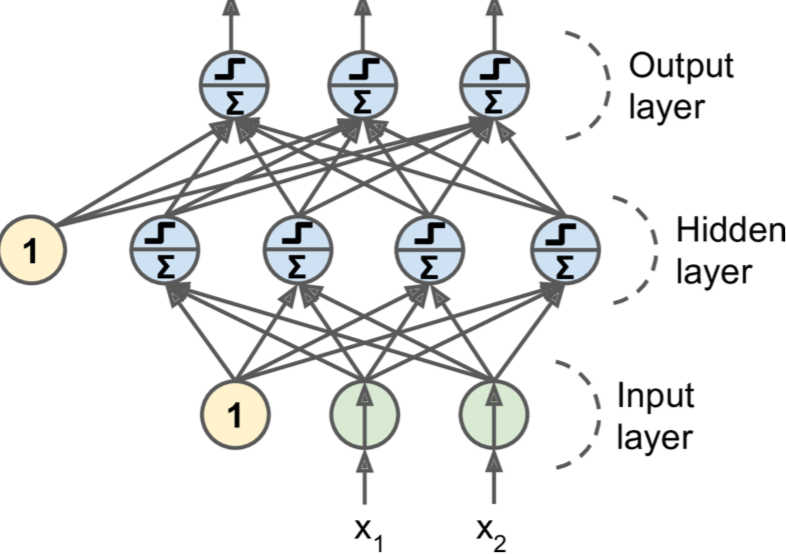
\(x => wx => f(x) =>uf(x) => f(uf(x))\)按照这个方式不断加深。
\(w_{ij}^l\)中l代表l-1到l层的权重,i表示第l-1层的第i个节点,j表示第l层的第j个节点。
\(z_i^l = \sum_{j=1}^Nw_{ij}^la_j^{l-1}+b_i^l\) 这里z表示第l层第i个节点,它由l-1层输出的线性组合而成。整层l的z用矩阵表示为\(z^l=W^la^{l-1}+b^l\)
所有的z会经过Sigmoid函数变为\(a^l\)
训练方式:Back Propagation,求梯度的方式称为reverse-mode autodiff。
从l层求解l-2甚至更前的层中的梯度w。一开始最底层w随机给定,然后结合数据一路算到最上层,记录每个节点运算的结果。然后从后往前求导数,一直到最前面。例如最右端,-0.53是通过后面节点的导数\(-1/x^2\),其中x为-0.53上面的1.37,乘上上一个梯度1得出的。
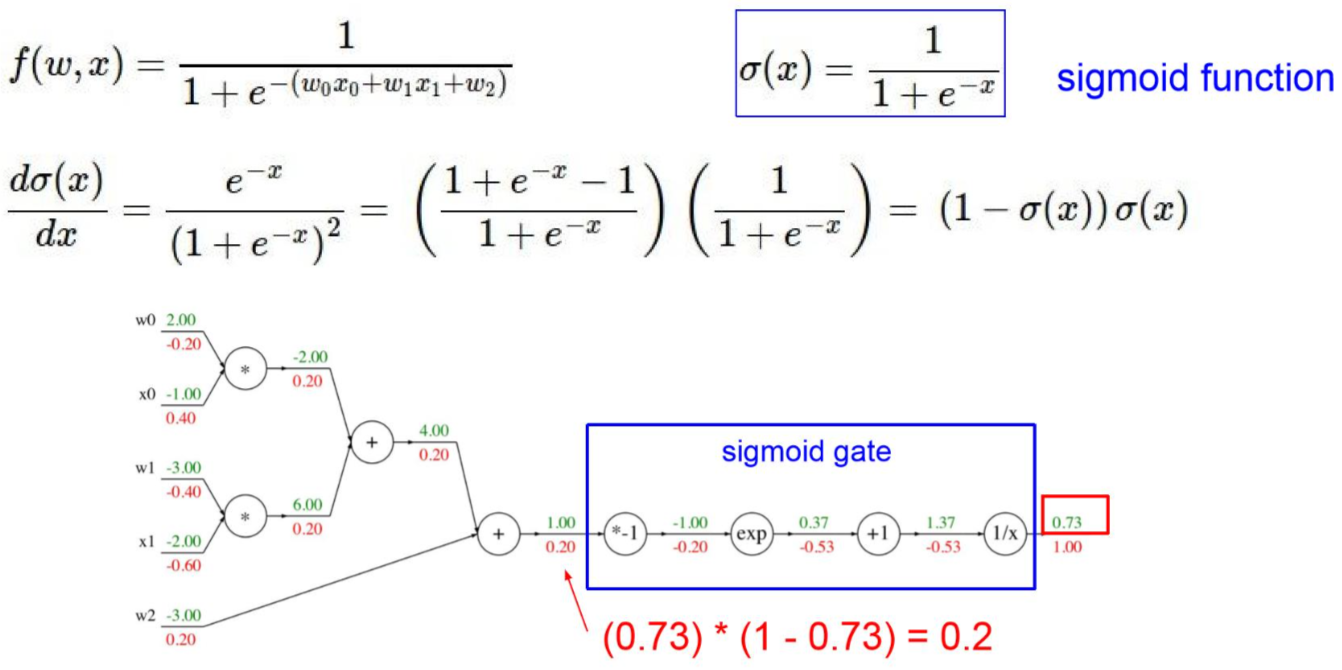
如上图所示,知道梯度后就可以根据\(w_i=w_i+\alpha \triangledown w_i\)对w进行更新。
feedforward neural network(FNN):signal flows only in one direction (from the inputs to the outputs)
DNN的挑战
Vanishing/Exploding Gradients Problems
vanishing:output layer到input layer越远,梯度越小,使得模型进步缓慢。
exploding:和vanishing相反,梯度越来越大,使得算法结果diverge而无法收敛,经常出现在RNN。
总的来说,DNN的梯度不稳定,具体来说是每层的进步相差很大。这个问题和过去使用传统的正态分布初始化权重和logistics作为激活函数有关。这两个设定下,variance在forward时越来越大,直到饱和。简单来说,当input的绝对值很大时,从logistics的图像可以知道,梯度是接近0的,这使得变换很难传递到底层。
Glorot and Bengio认为我们需要每层输出的方差等于其输入的方差,并且我们还需要梯度在反向流过一层之前和之后具有相等的方差。但除非layers具有相同数量的输入和输出连接,否则实际上不可能保证这两个条件。他们提出一个实用的方法:the connection weights must be initialized randomly。
| Activation function | Uniform distribution[-r, r] | Normal distribution |
|---|---|---|
| Logistic | \(r=\sqrt{6/(n_{inputs}+n_{outputs})}\) | \(σ = \sqrt{2/(n_{inputs}+n_{outputs})}\) |
| Hyperbolic tangent | \(r=4\sqrt{6/(n_{inputs}+n_{outputs})}\) | \(σ = 4\sqrt{2/(n_{inputs}+n_{outputs})}\) |
| ReLU(and its variants) | \(r=\sqrt{2}\sqrt{6/(n_{inputs}+n_{outputs})}\) | \(σ = \sqrt{2}\sqrt{2/(n_{inputs}+n_{outputs})}\) |
Nonsaturating Activation Functions
ReLU对于正数不会饱和,而且计算快。
dying ReLUs: during training, some neurons effectively die, meaning they stop outputting anything other than 0.当使用大的learning rate时更加常见。在训练期间,如果神经元的权重得到更新,使得神经元输入的加权和为负,则它将开始输出0。此时该神经元就死掉了,因为ReLU的输入为负数时,其梯度为0。
| Name | Equation | Comment |
|---|---|---|
| leaky ReLU | \(\max(\alpha z, z)\) | \(\alpha\)通常设置为0.01,0.2可能更好。至少神经元不会死掉,且有机会回复正常。 |
| randomized leaky ReLU (RReLU) | 训练时\(\alpha\)在一个范围内随机,测试时取训练时的均值。有点regularizer的效果。 | |
| parametric leaky ReLU (PReLU) | \(\alpha\)作为参数进行学习。一些研究发现对大规模的image数据效果相当好,而小数据则容易overfitting | |
| exponential linear unit (ELU) | \(α(exp(z)−1) \ \ \ if \ \ z<0;\\ z \ \ \ \ if\ \ z ≥ 0\) | \(\alpha\)表示z趋向负无穷时函数趋向的值。任何地方都平滑,包括0点,这能加快GD,因为在0处不会bounce。做预测时比较慢。 |
| SELU | \(\lambdaα(exp(z)−\alpha) \ \ \ if \ \ z<0;\\ \lambda z \ \ \ \ if\ \ z ≥ 0\) | 其中\(\lambda>1\)每层的输出将倾向于在训练期间保持相同的均值和方差。优于上述,它解决了vanishing/exploding问题。 |
一般来说,SELU > ELU > leaky ReLU(及其变体)> ReLU > tanh > logistic。 如果非常关心运行时性能,那么leaky ReLU可能优于SELU。 如果不想调整另一个超参数,可以使用默认α值(leaky ReLU为0.01,ELU为1)。 如果有空闲时间和计算能力,可以使用交叉验证来评估其他激活函数,特别是如果NN过度拟合则使用RReLU,或者如果您拥有庞大的训练集,则为PReLU。
Batch Normalization
在FNN中,如果不使用SELU,则一般需要BN来防止vanishing/exploding在训练期间出现。随着前一层参数的变化,每一层输入的分布在训练期间都会发生变化。该技术在每个层的激活函数之前添加操作,简单地将输入zero-centering and normalizing,然后每层使用两个新参数缩放和移位结果。 换句话说,此操作可让模型了解每层输入的最佳缩放比例和平均值。这两个参数值都是根据每批数据计算得到的。一共四个参数需要学习:γ(scale), β (offset), μ (mean), and σ (standard deviation)
在测试的时候则直接用训练样本的总均值和方差。
利用这个方法连会饱和的函数都可以使用,也可以使用更大的学习速度,而且有一定的regularization的作用。当然,这也会减慢预测速度。
模型建立
ransfer learning:找到一个现有的神经网络来完成与你想要解决的任务类似的任务,然后重用这个网络的下层。Model Zoos
Freezing the Lower Layers、Caching the Frozen Layers
Tweaking, Dropping, or Replacing the Upper Layers:首先尝试冻结所有复制的图层,然后训练模型并查看其执行情况。 然后尝试解冻一个或两个顶部隐藏层,让反向传播调整它们,看看性能是否有所改善。数据量限制了层数,所以在缺乏数据时,有时需要删除顶部隐藏图层并再次冻结所有剩余的隐藏图层。反之数据量多也可增加层数。
Unsupervised Pretraining:在label数据不足的情况下:
1.Unsupervised Pretraining,using an unsupervised feature detector algorithma (autoencoders)来逐层训练层,从最低层开始然后向上移动。
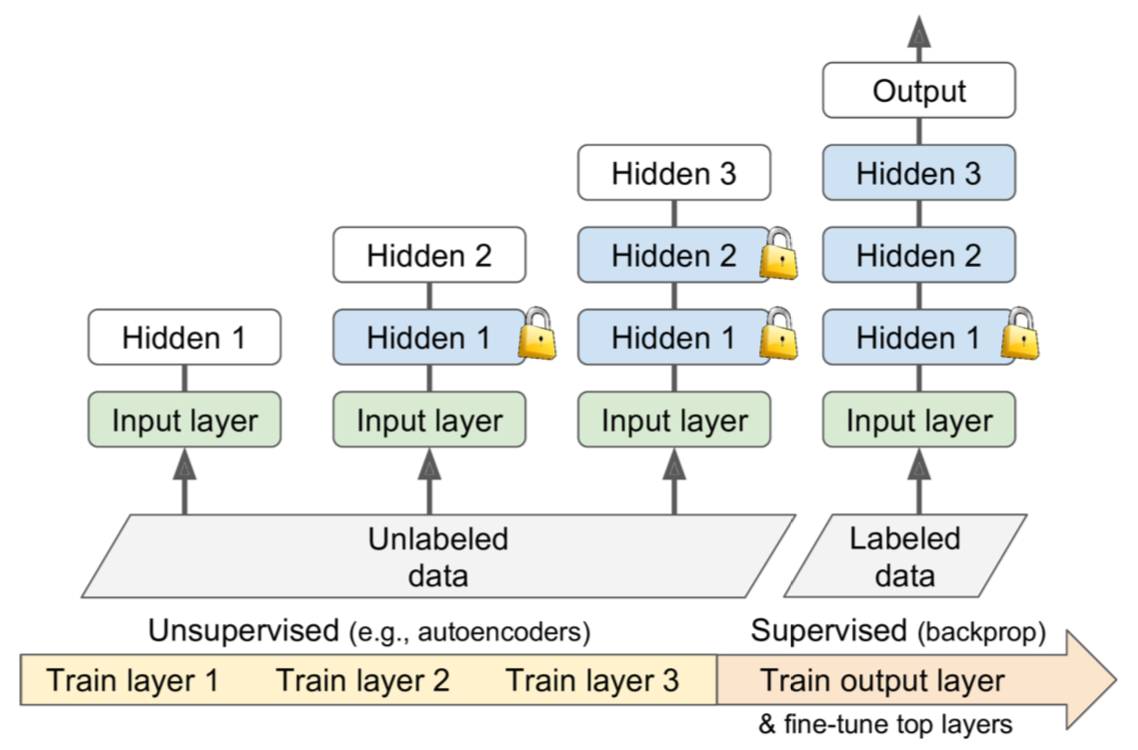
2.Pretraining on an Auxiliary Task:在辅助任务(可以轻松获取或生成标记的训练数据的任务)上训练第一个神经网络,然后重复使用该网络的较低层来完成您的实际任务。又或者将所有训练样本标记为“good”,然后通过破坏好的训练实例来生成许多新的训练实例,并将这些已损坏的实例标记为“bad”。还有一种方法:训练第一网络以输出每个训练实例的分数,并使用成本函数来确保good实例的分数比bad实例的分数大至少一些余量(margin)。
模型训练
Faster Optimizers
提高训练速度的方法:a good initialization strategy for the connection weights, using a good activation function, using Batch Normalization, and reusing parts of a pretrained network。另外一方面是使用更快的optimizer,而非常规的GD。
这些optimizers包括:Momentum optimization, Nesterov Accelerated Gradient, AdaGrad, RMSProp, and finally Adam optimization. 就目前而言,最后的Adam是最好的选择。
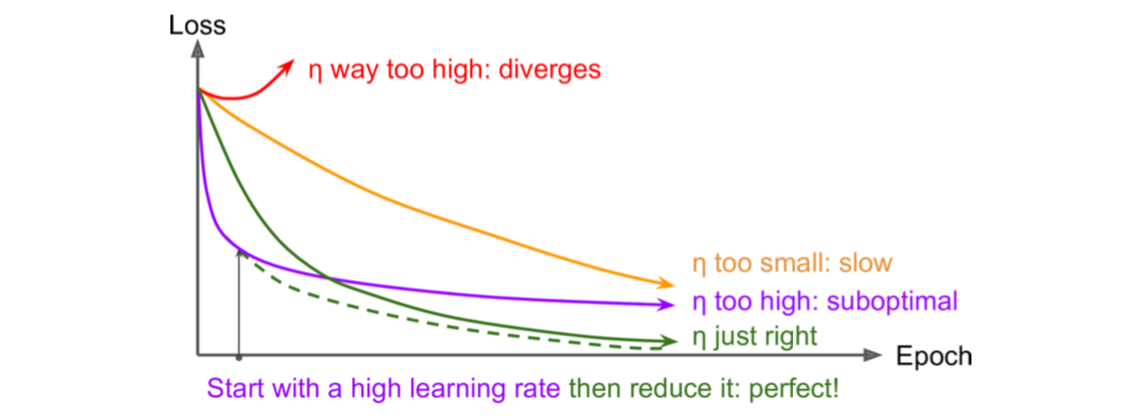
Learning Rate Scheduling
实际使用中,AdaGrad, RMSProp, and Adam optimization在训练时会自动减少learning rate,其他optimization才需要这部分调优。
模型优化
Fine-Tuning Neural Network Hyperparameters
NN可以调节的超参太多了:
- network topology (how neurons are interconnected)
- the number of layers
- the number of neurons per layer
- the type of activation function to use in each layer
- the weight initialization logic
一些选项包括randomized search、Oscar。
层数:即便只有一层hidden layer,只要有足够的neurons,效果依然很好。但是更多的层数可以指数式地减少neurons的数量,并提高训练速度。实际数据通常以分层方式构建,DNN便是利用这一事实:较低的隐藏层模拟低级结构(例如,各种形状和方向的线段),中间隐藏层组合这些低级结构来模拟中间层结构(例如,正方形,圆形),最高隐藏层和输出层将这些中间结构组合以模拟高级结构(例如,面)。除此之外,NN的结构还有利于模型的组合,比如某部分NN学习了人脸的识别,那么可以在这个NN的基础上构建识别发型的NN。因此,还可以将各部分的训练分开,从而避免极大量数据训练一个极大的DNN,而是可以并行地利用相对较少的数据训练不同部分的模型。
每层的neuron数量:通常设置比所需的layers和neurons更多的数量,然后采用early stop防止overfitting。
激活函数:通常使用ReLU或者它的变种。这种函数不会在高点饱和(只要输入值够大),而logistic和hyperbolic tangent会在1饱和。在输出层,logistics for binary, softmax for multiclass, no activation func for regression
Avoiding Overfitting Through Regularization
Early Stopping
l1 and l2 Regularization
dropout:在每个训练步骤中,每个神经元(包括输入神经元但排除输出神经元)有概率p暂时“退出”,这意味着在此训练步骤中它将被完全忽略,但它可能在下一步“激活”。超参数p称为丢失率,通常设置为50%。 训练后,神经元不再被丢弃。
Max-Norm Regularization:for each neuron, it constrains the weights w of the incoming connections such that \(∥w∥_2 ≤ r\), where r is the max-norm hyperparameter and \(∥ · ∥_2\) is the l2 norm. We typically implement this constraint by computing \(∥w∥_2\) after each training step and clipping w if needed (\(w= w\frac{r}{∥w∥_2}\)).Reducing r increases the amount of regularization and helps reduce overfitting. Max-norm regularization can also help alleviate the vanishing/exploding gradients problems (if you are not using Batch Normalization).
Data Augmentation:从现有训练实例中生成新的训练实例,人为地增加训练集的大小。通常最好在训练期间动态生成训练实例,而不是浪费存储空间和网络带宽。TensorFlow offers several image manipulation operations such as transposing (shifting), rotating, resizing, flipping,
and cropping, as well as adjusting the brightness, contrast, saturation, and hue.
add skip connections:DRN再说。
参考:
Hands On Machine Learning with Scikit-Learn and TensorFlow
http://cs231n.github.io/optimization-2/ (Stanford CS231n, Fei-Fei Li)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号