机器学习总结（未完）

机器学习理论

目录

概念

Discriminative and Generative Learning

前者：寻找分类面，拟合条件概率，即x => y，然后减少损失函数。例如线性回归、决策树、SVM、KNN

后者：例如HMM、Naive贝叶斯、GMM、LDA

  • 学习过程：寻找数据分布，拟合联合概率，Fit a probability distribution to each class, individually. Aim to recreate how the observed data are generated following some hidden patterns (or rules).
  • 分类过程：Which of these distributions was the observation most likely to have come from? 每一个observation都是不同类别分布的混合。

通用

流程

  1. Frame the problem and look at the big picture.
    目标决定评估指标、模型怎么用决定模型类型、过往经验
  2. Get the data.
    类和量、空间、合法性、创建工作空间、sample测试集(shuffle the training set)
  3. Explore the data to gain insights.
    专家建议、copy、研究（数据类型、缺失、噪音、分布）、identify target feature
  4. Prepare the data to better expose the underlying data patterns to Machine Learning algorithms.
    filtering, cleaning (outliers, missing values), feature selection, engineering(discretize continuous features, decompose, log/ sqrt etc. transformation, aggregate), scaling
  5. Explore many different models and short-list the best ones.
    每个模型最好的变量、各模型的错误类型（怎么解决）、选出犯不同错误的模型
  6. Fine-tune your models and combine them into a great solution.
    missing values的处理视为超参数， 调参（random, grid search, Bayesian optimization）, 组合模型
  7. Present your solution.
    Document what you have done, assumptions and limitations, Explain why your solution achieves the business objective. what worked and what did not
  8. Launch, monitor, and maintain your system.
    Launch: plugging the production input data sources into your system and writing tests
    Monitor: write monitoring code to check your system’s live performance at regular intervals and trigger alerts when it drops (models tend to “rot” as data evolves over time)
    evaluate the system’s input data quality
    maintain: train your models on a regular basis using fresh data
    If your system is an online learning system, you should make sure you save snapshots of its state at regular intervals so you can easily roll back to a previously working state.

评估与选择

训练集和测试集合的划分

留出法

2/3～4/5作为training set，剩余作为test set。问题：估计不稳定。

Cross-Validation

Leave-one-out cross-validation (LOOCV) 能准确确定针对训练数据的最优flexibility和错误率。问题：如果下面公式不成立（通常是非线性模型），则很耗时，高variance。

\[CV_{(n)} = \frac{1}{n}\sum_{i=1}^{n}(\frac{y_i-\hat{y}_i}{1-h_i})^2 \]

上面公式中\(h_i\)为leverage statistic（在之前high leverage points有应用），它所在的分母的值介于1/n和1，反映了某观测值的leverage对他所fit的模型的影响，即这个分母是用于抵消观测值的leverage的。

k-Fold Cross-Validation（LOOCV的特例）相对省时，可大致确定最优flexibility，适中的variance。如果超过一轮，考虑对数据shuffle。问题：不能较为准确地评估错误率。

Bootstrap

用于测量某个对象的标准差，比如系数，且使用范围广。方法是从原始数据集中，通过重复抽样产生多组与原始数据集相同大小的数据集，然后估计这些数据集的某个指标，比如均值\(\hat{\mu}_i\)，最后利用\(\hat{\mu}_i\)和他们的均值来求出SE(\(\hat{\mu}\))。

也可利用到training set和test set，因为一般而言会有1/3的原始数据没有被抽取，这部分可用于测试。

性能测量

正确判断 错误判断
正例 TP FN(cost01)
反例 FT(cost10) TN

准确率

这会受到样本组成的影响。例如，如果样本中只有一个类别，那么不考虑数据，直接只选取该类别的模型的准确率将是100%。

查准率、查全率和F1

查准率precision：判断“是”的里面，有多少是正确的。

查全率recall：正例有多少被正确预测。

P-R图直观地显示出学习器在样本总体上的查全率、查准率。若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”，则可断言后者的性能优于前者。如果PR曲线有交点，考虑F1：

\[F_\beta=\frac{1+\beta^2 \times P \times R}{(\beta^2 \times P)+R} \]

\(\beta=1\)时查准率和查全率权重一样，<1时更重视查准率，反之。

ROC与AUC

TPR：和recall一样。

TNR：在所有为“假”的对象集里面，会判断出多少个“真”

AUC为ROC曲线的下方的面积。

PR和ROC都要权衡，看目标。you should prefer the PR curve whenever the positive class is rare or when you care more about the false positives

代价敏感错误率与代价曲线

Cost-sensitive：\(E=\frac{1}{m}(\sum I(f(x_i) \ne y_i)cost_{01}+\sum I(f(x_i) \ne y_i)cost_{10}))\)，基于此可以定义其他性能指标的代价敏感版本，甚至基于多分类问题。

ROC曲线不能直接反应学习器的期望总体代价，而代价曲线可以。

比较检验

即便有了性能指标，比较不同模型的效果最好还是在此基础上通过假设检验推断比较好。因为测试集和现实数据有差别、测试集能以保证完全相同，模型的生成本身也有随机性。

针对单个模型：cross validation后构建t分布，根据给定的置信度判断

两模型之间：在cross validation中，每一轮测试都计算两个模型的错误率的差，并最后计算均值和方差构建t分布。如果超过1轮，则考虑shuffle，而且只取每轮的第一折的均值，方差在每一折都计算。

多模型之间：两两比较或者Friedman检验。

其他检验参考西瓜书：McNemar检验、Friedman检验

偏差与方差的权衡

test MSE的期望可分解如下：

\[E(y_0 − \hat{f}(x_0))^2 = Var(\hat{f}(x_0)) + [Bias(\hat{f}(x_0))]^2 + Var(ε). \]

所以，为了最小化expected test MSE，需要减少variance and bias。

variance表示利用不同training set评估模型时产生的差异。一般情况下，越flexible的模型，variance越大，因为过度专注于训练数据。bias高可能是模型不够flexible，无法拟合数据。

随着flexibility的增加，variance / bias先减少后增加。

特征

Feature类型：Nominal定类（如性别），Ordinal定序（教育程度），Continuous。

离散化：

  • 对Ordinal：Static，定值划分。Dynamic根据当前数据的范围/数据频率/clustering等指标划分
  • 对Nominal：binary划分，如决策树。可选出IG最大，但耗费CPU。

binary划分有时也适合Ordinal，如年龄段中，小孩和老人被分为一类。

标准化

  • Z-Score：\((x-\mu)/\sigma\)
  • 最大最小标准化：\((x-x_{\min})/(x_{\max}-x_{\min})\)
  • 小数定标法：\(x/10^k\)，其中k为max(|x|)的数位

样本

类不平衡

两个办法：过采样（SMOTE）或欠采样（去掉部分多数类的样本）

SMOTE算法：

  1. 从少数类的全部样本中找到\(x_i\)的k个近邻（例如用欧氏距离）

  2. 从这k个近邻中随机选择一个样本\(x_i'\)，根据公式\(x_{i \ new}=x_i+rand * (x_i'-x_i)\)得出新的样本。

  3. 重复n次，针对每个少数类样本新增n个新样本

算法问题：如果负类样本分布在边缘，这种新增样本会使分布偏向边缘，增大模型分类的难度。

具体算法

线性回归

目标函数：L2 或 L1

L0 到L∞

0是找向量有多少维不为0。

1为绝对值和

2为平方和开根

∞为最大值

\(||x||_p = (\sum_{i=1}^{n}|x_i|^p)^{1/p}​\)

解法：Normal Equation或GD

  • Normal Equation：数据量大时训练很慢，比如大于10w。因为需要计算逆矩阵，这相当耗时。其他转置，相乘之类的只需O(n)。

    目标函数是\(\min ||X\Theta - Y||^2\)，化简可得\(\Theta=(X^TX)^{-1}X^TY\)

    提示：\(||X||^2=X^TX\)， \(\frac{d(U^TV)}{dx}=\frac{d(U^T)}{dx}V+\frac{d(V^T)}{dx}U\)， \(\frac{\partial(U^TBV)}{\partial x}=\frac{\partial(U^T)}{\partial x}BV+\frac{\partial(V^TB^T)}{\partial x}U\)

    上述求法需要满足数据中的特性不存在线性相关，且特征少于数据量。在实现中，为了解决这类问题，需要一些调整，例如加上L2的regularization。其结果会变为\(\Theta=(X^TX+\lambda I)^{-1}X^TY\)， 这里的I是(1,1)和非对角线位置为0（左上角为0是\(\theta_0\)不需要加惩罚的意思）。通常加了这个矩阵后，很多不可逆矩阵就变成可逆了。

    sklearn的LinearRegression用的是pseudoinverse. Its time complexity is O(n2) and it works even when m<n or when some features are linear combinations of other features. All the data must fit in memory, it does not require feature scaling and the order of the instances in the training set does not matter

    • 从概率的角度，利用极大似然求解。假设X服从正态分布，且各数据互相独立。那么在极大似然函数下，就是给定X和Y，求\(\theta\)能使\(p(\vec{y}|X;\theta)\)最大。而从推到结果来看，使L最大实际上也是使\(y^{(i)}-\theta^Tx^{(i)}\)最小，所以目标跟上面的是一致的。

      \[L(\theta)=L(\theta;X,\vec{y})=p(\vec{y}|X;\theta)=\prod_{i=1}^{m}p(y^{(i)}|x^{(i)};\theta)=\prod_{i=1}^{m}\frac{1}{\sigma \sqrt{2\pi}}exp[-\frac{1}{2}(\frac{y^{(i)}-\theta^Tx^{(i)}}{\sigma})^2] \]

  • Gradient Descent

    和上面类型，求\(L=\frac{1}{2N}\sum_{i=1}^{N}(h(x^{(i)})-y^{(i)})^2\)的最小值。求导数得出变化方向。

    \[\frac{\partial{L(\Theta)}}{\partial \theta_j} = \frac{1}{N}\sum_{i=1}^{N}(h_m(x^{(i)})-y^{(i)}) x^{(i)}_{j} \]

    利用\(\theta_j-\alpha\frac{\partial{L(\Theta)}}{\partial \theta_j}\)更新\(\theta_j\)。更新有下面三种方式。然后得出新的L，并不断重复，知道新L和就L差距小于某个阈值。

    如果加上L2的regularization，函数可表示为：\(L=\frac{1}{2N}||X\theta-Y||^2_2+\frac{1}{2}\alpha||\theta||^2_2\)。同样求导后，\(\theta\)的更新函数变为\((1-\frac{\alpha \lambda}{N})\theta_j-\alpha(\frac{1}{N}\sum_{i=1}^{N}(h_m(x^{(i)})-y^{(i)}) x^{(i)}_{j})\)。所以实际上每次GD是在\(\theta\)经过shrinkage后再调整的。

    1. jump out of local minima

      对irregular function有好处。一般解决方法是simulated annealing，即learning rate由大到小，learning schedule是决定learning rate变化的函数。Stochastic GD and Mini-batch GD would also reach the minimum if you used a good learning schedule.

    2. the cost function will bounce up and down, decreasing only on average

    3. If the algorithm shuffle the training set, then go through it instance by instance, then shuffle it again, and so on. This generally converges more slowly than don’t shuffling.

    4. if you divide the tolerance ϵ by 10 (to have a more precise solution), then the algorithm will have to run about 10 times more iterations

    5. 不适合复杂的非线性函数问题

Algorithm Large m Out-of-core support Large n Hyperparams Scaling required Scikit-Learn
Normal Equation Fast No Slow 0 No LinearRegression
Batch GD Slow No Fast 2 Yes n/a
Stochastic GD Fast Maybe Fast ≥2 Yes SGDRegressor
Mini-batch GD Fast Maybe Fast ≥2 Yes n/a

Linear Model Selection and Regularization

Shrinkage Methods

使用前记得standardizing。参数的权重过度，容易overfitting，所以需要加上一个\(\beta\)的惩罚系数，而所有\(\theta\)的组合形式一般分为L2和L1，对应Ridge和Lasso。数学上表示为：minimize RSS subject to \(\sum_{j=1}^{p}\beta_j^2 ≤ s\) or \(\sum_{j=1}^{p}|\beta_j| ≤ s\) ，利用拉格朗日函数构造出新的损失函数。

  • Ridge Regression：它优于最小二乘法在于它的bias-variance trade-off，即它在test set中表现得更好。解法参考上面。

  • Lasso Regression：能够去除一些不显著的变量，这一般通过图像来理解。L1的几何形式通常会让交点处在坐标轴上（sparse解），从而使部分参数变为0。解法：

    • Coordinate Descent：固定其他参数，然后调整\(\beta_i\)，找出梯度最小的\(\beta_i\)，然后调整另外一个参数，最终会靠近最优解。
    • Forward Selection：先沿一个维度的方向走，然后到下一个，只要L是减少的。这种方式时间复杂度比较高。
    • Forword Strategies：试探各个维度的方向，找出L减少最多的走。
    • Least Angle Regression：2和3的折衷，先沿一个维度走一步，然后沿所有方向等比例走。

  • Elastic Net：Ridge和Lasso的混合

两者适合的场景取决于有多少个无用的predictors，由于各个predictors的作用是未知的，所以一般用cross-validation来确定选择。

Logistics regression

将多元线性回归用于二分类问题，可以利用Sigmoid函数\(\frac{1}{1+e^{-Z}}\)，将回归数值限定在0～1之间。这个Sigmoid实际上由odd log，即左边的函数推到得到。左边是比较0和1各自出现概率的比，而两概率之和为1。这样就能把各是0.5的情况反应为\(-\theta^TX=0\)，而其中一个概率极大，另一个概率也就极小，同样能反应为正负无穷大。

\[log(\frac{p(X)}{1-p(X)})= -\theta^TX \ \ \ \ \ \rightleftharpoons \ \ \ \ \ p(X) = \frac{1}{1+e^{-\theta^TX}} \]

案例：情感分析（正/负面）

TF-IDF：频率和区分度（文档数/包含该词的文档数）。统计所有文章的词，求出这些词的TF-IDF作为x，然后通过训练计算出各个词的权重，即情感强度。之后就可以对一些新的评论进行情感分析了。

目标函数（交叉熵）：下面j表示class，只有0和1两种情况。I表示预测正确时返回1，反之-1。\(\sum log\)实际上时有P的累积转化而来，所以P的总和越大，L越小。下面函数里是log的乘法和加法，属于凸函数，所以可以通过GD来求解。

\[L(\theta) = -\frac{1}{N}[\sum_{i=1}^{N}\sum_{j=0}^{1}I(y^{(i)}=j)logP(y^{(i)}=j|x^{(i)}, \theta)] \]

交叉熵损失函数通常用于求值与概率相关的情况，如果求值是具体数值，如价格等，一般用L2，差值的比例也是一个选择。

对于两类以上的分类问题，可以对sigmoid作一些调整。

Softmax：例如有（1, 2, 3）类，先(1, (2, 3))分为两类回归得出\(\theta_1\)，然后(2, (1, 3))分为两类回归得出\(\theta_2\)，类推。然后对于一个数据x，分别计算它属于各类的概率，代入下面公式得出结果。

\[p(y^{(i)}=k|x^{(i)};\theta) = \frac{exp(\theta_k^Tx^{(i)})}{\sum_{j=1}^{K}exp(\theta_j^Tx^{(i)})} \]

KNN

Return the most common label amongst them. 函数以及参考个数k。

  • distance functions：需要满足4个条件（nonnegativity, symmetry, triangle inequality可提高寻找的速度, constancy of self-similarity）。例子：L1, L2, Cosine Similarity, Hamming distance(XOR), Edited Measure(某个特征相等，相似度+1), shape context等等。
  • k：k过小过度拟合。

目标函数：无。设置好k和distance func后模型就决定了

分类/回归过程：以L2为例，对于新数据\(x\)，从训练集中找出它最近的k个\(x^{(i)}\)，距离判断为\(\sqrt{\sum_{K}(x_k-x'_k)^2}\)。然后看这k个\(x^{(i)}\)类别的众数/距离加权等方式判断x为哪一类。在预测中求\(x^{(i)}\)的均值等方式得出回归值。

一般思路的代码实现时间复杂度较高，可参考：Locality sensitive hashing, Ball trees, K-d trees等实现。

线性回归 vs KNN：两者的选择一般由数据的线性程度来决定。然而，当predictor较多时，即便是非线性数据，线性回归依然会比KNN好，这是由于curse of dimensionality。当数据是高维度时，non-parametric需要更多的样本来拟合。

Kernel Density Estimation（KDE）

分类或回归参考的数据点可以从k个变为所有数据，每个数据点也可以有相应的权重。

Kernel Func：构建时K(x1, x1)=1, K(x1,x2)=0，那么||x1-x2||=∞。例如Nadaraya-Watson Kernel：

\[\hat{y}=\frac{\sum_{i=1}^NK(x^*-x^{(i)})y^{(i)}}{\sum_{i=1}^NK(x^*-x^{(i)})}\\ K(x^*-x)=\exp(-\frac{1}{2\sigma^2}(x^*-x)^2) \]

此处\(\hat{y}\)是服从正态分布的。

Gaussian Processes

\[f(x)～ GP(m(x),K(x,x'))\\ m(x)=E[f(x)]\\ K(x,x')=E[(f(x)-m(x))^\top(f(x')-m(x'))] \]

将数据看作是一个高维的高斯分布。比如有一个k维的y，那么y服从一个k维0和k x k的协方差矩阵的高斯正态分布。然后利用Kernel Func计算协方差矩阵。比如定义Kernel Func为\(K_{i,j}=\exp(-\lambda||x^{(i)}-x^{(j)}||^2)\)，这就能计算矩阵中各(i,j)的值。当有一个新数据需要估计时，协方差矩阵就也需要变化，可以根据边缘概率计算。最终可计算出这个数据的均值和方差，从而在预测上给予一个范围的估计。

作为Non-parametric Model，目的是尽量从当前数据得出结果，而不涉及过去经验。在对现象没有任何可靠类似的模型和分布时，这类模型可作为一个基准。

Naive Bayes

\(P(Y|X_1,...,X_n)=\frac{P(X_1,...,X_n|Y)P(Y)}{P(X_1,...,X_n)}\)

此处是给定数据X，它有n个特征，在这些特征下，Y出现的概率。由于Naive假设所有特征独立，那么\(P(X_1,...,X_n|Y)\)可化简为\(\prod_{i=1}^nP(X_i|Y)\)（有时会取log，因越乘越小）。这样根据历史数据计算出各部分的值就能算出目标概率。

目标函数：无。

案例：Spam Filtering

思路：一个X数据相当于一个map，记录各个单词的数量。每个map的key数量相同。如果邮件中出现这些key之外的单词，则需要作出调整，比如返回P(Xi|Y) = 1/v（v为key的数量）。

Decision Tree

建树过程：根据条件不断划分数据，直到达到一定条件。所以需要划分标准和停止条件。

划分方式和选择：方式有binary和multi-way，根据下面的目标来选择划分。

分类树目标函数impurity：

  • 信息论与Entropy

    信息函数：H(x) = -logP(x)。这出于三个点考虑：1）信息量与出现概率成反比。2）信息量可相加。3）信息量大于等于0。

    Entropy：E[H(x)]。集合X的Entropy越大，不同类的X数量越接近，反之。例如x1=0.5, x2=0.5时等于1，而只有一种X时，默认为Entropy=0。

    IG（information gain）：原始Entropy与分割后Entropy权重和的差，即\(IG = OriEntropy -∑\frac{A_i}{A}Entropy(A_i)\)

    目标：选取使IG最大的分割。因为IG大，说明分割后的Entropy权重和小，即子集合更pure

  • Gini

    \(GINI(t)=1-\sum_{j}p(j|t)^2\) 注意这里p(j|t)是class j在node t 的占比。

    \(GINI_{split}=\sum_{i=1}^{k}\frac{n_i}{n}GINI(i)\) 其中ni为第i个子节点的数据量，n为当前节点的数据量。

    目标：选取GINI split最小的分割。这由权重和GINI(t)决定，权重越大，GINI(t)越小，说明越多的数据被划分到更pure的集合。

  • Error

    \(Error(t) =1- \max_i P(i|t)\)

由于分类错误率对树的成长不敏感，所以一般用前两个。而Entropy产生的树可能更平衡，但后者会快一点。最后还是根据实际效果来决定。

回归树的目标函数：

  • L2：按照binary split的思路，先针对一个维度\(j_i​\)，然后在这给维度上找点s，该点把数据分为R1和R2两个区域。此时计算各区域的y(i)的均值\(C_i​\)域各y的L2距离。在当前维度下循环取不同的s，直到Cost Func最小。此时变决定了\(j_2​\)的s，接下来就是其他维度的s了。当所有维度都决定好后，看哪个维度的划分能够使Cost Func最小，如果\(j_2​\)效果最好，那么就采用该维度的s来划分数据，得出两个子节点。之后子节点的划分就不用找\(j_2​\)了，找剩余维度的s。

    \[\min_{j,s}[\min_{C1} \sum_{x\epsilon R_1}(y^{(i)}-C_1)^2 + \min_{C2}\sum_{x\epsilon R_2}(y^{(i)}-C_2)^2] \]

决策树无需scaling和centering。

通常会设置一个 \(\alpha\) 来作惩罚系数，防止过度拟合。

剪枝

前置剪枝：建树提前结束。效果比后置差，训练快。

后置剪枝：树建好后，1）用单一叶子节点替代整个子树，叶子节点分类采用子树中最主要的分类；或2）将一个子树完全替代另外一颗子树。将效果好，训练慢。

单树的优缺点：易于解释和运用，但对样本数据的变化很敏感，且效果一般。

Bagging and Boosting

树够多的话，前两个不会overfitting

Bagging

bootstrap：从原数据中有放回地进行抽样，从而产生多组数据集来建不同的决策树。这种抽样可以减少原数据集中极端数据的影响（如前面所说，决策树对样本数据敏感），因为极端数据数量少，被抽取的概率就低。在多棵树的情况下，对于回归，取树的均值；对于分类，最多投票的class。

Random Forests就是通过这种方式实现的。

Out-of-Bag (OOB) Error Estimation

变量重要性测量：某变量的划分对RSS/Gini or entropy减少的总量

Adaptive Boosting

  1. 初始化，每个数据的权重\(w^{(i)} = 1/N\)
  2. 训练
  3. 计算模型权重：计算每个模型的错误率ek，并设置权重\(\alpha_k=\frac{1}{2}\ln(\frac{1-e_k}{e_k})\)。这个函数能使错误率为0.5时权重变为0。
  4. 更新数据权重：提高出错的样本的权重，\(w_{k+1}^{(i)}=\frac{w_k^{(i)}}{Z_k}\exp(-\alpha_ky^{(i)}G_k(x^{(i)})\)。这个函数中G为模型k预测的结果，如-1，如果\(y^{(i)}\)也是-1，那么就是预测正确，权重会增大。而\(Z_k\)是用于normalization，即然样本的权重和为1。
  5. 循环2～4.

假设设置了k个模型，那么经过一次训练，就有了k个带有权重的模型。再一次训练就有2k个带有权重的模型，如此类推。最优决策通过投票或均值。

Boost不能并行。

GBDT

\(f_{m+1}(x)=f_m(x)+T(x)\) 这条函数表示，在前一个模型的基础上，再训练一个，即h，从而达到一个新的F。这个模型T的训练目的就是让\(f_{m+1}(x^{(i)})-y^{(i)}\) 最小。实际上，在有了上一个模型的基础，下一个模型拟合的是新的残差。

基于回归树，损失函数为L2，在设定好M，即决策树的数量后

  1. 初始化\(f_{0}(x)=0​\)

  2. 计算残差$r_{mi}=y_i-f_{m-1}(x_i) $，i为第i个数据。

  3. 根据\(\hat{\theta}_m =\arg \min\sum_{i=1}^N [r-T_m(x|\theta_m)]^2\)，训练出第m棵决策树。

    \(T_m=\sum_{j=1}^{J}c_jI(x\epsilon R_j)\) ，其中cj为第m棵树在第j个区域中判断出的常量。决策树把数据X分为了J个区域，每个区域一个值，或者说J个节点，每个节点一个值。

  4. 更新\(f_m(x)=f_{m-1}(x)+\alpha T_m(x|\theta)\)， T为第m棵决策树。在调整f时，通常会对T乘上一个学习速度\(\alpha\)，通常是0.001到0.01，来降低拟合速度，避免错过了最优。

  5. 重复2～4，直到建立起M棵树，得出\(f_M(x)=\sum_{m=1}^{M}T(x|\theta)\)

sklearn中的GBDT参数：

  • 树数量：一般40～70
  • 学习速度：一般0.05～0.2
  • max_depth：数据量大树，限制5～30
  • min_sample_split：样本少的不用管（少于1w）。样本的0.5～1%，不均等的分类可以取小的
  • min_samples_leaf：样本少的不用管。如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。

SVM

在有约束的条件下求最优解，可利用拉格朗日函数把两者结合到一起，会得出\(L(x, \lambda) = f(x)+\lambda g(x)\)，其中g为约束条件函数，是原约束化为<=0或=0的形式后的函数（求最小值时+\(\lambda\)，且\(\lambda> =0\)）。

等式约束求解：

当g(x) = 0，只需分别向x和\(\lambda\)求偏导就能得出最优解的两个条件。即\(\nabla_xf(x)+\lambda \nabla_x g(x)=0\) 和 \(g(x)=0\)。第二条是原本设定的，第一条的原理是让两个梯度平行。此处的原理是，先让所有候选x解都满足约束，然后沿着与f(x)负梯度（f(x)移到等号左边就成负梯度了，\(\lambda\)相当于移动幅度）成锐角的方向移动，此时f(x)的值会不断减少。而当f(x)负梯度与x移动方向成直角时就不能再减少了。而g(x)的梯度是一直与x的移动方向垂直的，因为沿着g(x)移动，意味着一直等于0，而与原方向垂直的方向才能最大地改变等于0的情况。所以最后，g(x)的梯度也就与f(x)的梯度平行了。

不等式约束求解（KKT）：

当g(x) <= 0，拉格朗日的求解条件变为4条：\(\nabla_xf(x)+\lambda \nabla_x g(x)=0\) , \(\lambda>=0\), \(\lambda g(x)=0\), \(g(x)<=0\)。这四个条件能够把最优解是否在约束范围内的两种情况包含进去。当\(\lambda=0\)时，最优解在约束范围内，第一条等式就只剩下求f(x)的最小值了。如果\(\lambda > 0\)，那么g(x)就只能等于0了，此时就和等式优化一样了。按照这个套路来解，最终\(\lambda\)要从0和另一个表示\(\lambda\)的数中选择。实际上是取max。所以下面解svm时，拉格朗日可变为minf(x) max(\(\lambda\))的函数。

基于下面的函数：

\[\min_w \frac{1}{2}||w||^2\\s.t.\ \ y^{(i)}(w^\top x^{(i)}+b)\geqslant1 \]

w为垂直于分割线的向量。它由\(\max 2/||w||\)转化而来，而这个max是通过下面推导得到。首先分割线\(w^\top x^{(i)}+b\)是否大于0来判断数据属于哪一类。根据分割线和距分割线其最近的点的距离来给所有点进行缩放，可以得出\(w^\top x^{(i)}+b\)大于等于1或小于等于-1来判断类别。另外，\(w^\top\)实际上是和分割线垂直的（画图可知）。所以从距离分割线最近点出发的向量\(\lambda w\)找到另一边距离分割线最近点（关于分割线对称），此时两点距离构成了最宽的margin，其宽度为向量的模，即\(\lambda||w||\)。另外，根据\(w^\top x_1+b=1, w^\top x_2+b=-1, x_2 = x_1+\lambda w\)，对称的两个点，可以解得margin为2/||w||。

（1）求解的拉格朗日方程为

\[\min_{w,b}\max_{\lambda_i}L = \frac{1}{2}||w||^2+\sum_{i=1}^{N}\lambda^{(i)}[1-y^{(i)}(wx^{(i)}+b)]\\ \frac{\partial L}{\partial w} = 0 \ \ \ =>\ \ \ w-\sum \lambda^{(i)}y^{(i)}x^{(i)}=0\\ \frac{\partial L}{\partial b} = 0 \ \ \ =>\ \ \ \sum \lambda^{(i)}y^{(i)}=0 \]

部分求解过程

\[\frac{1}{2}w^\top w = \frac{1}{2}(\sum_{i=1}^{N} \lambda^{(i)}y^{(i)}x^{(i)})^\top(\sum_{j=1}^{N} \lambda^{(j)}y^{(j)}x^{(j)}) \]

由于之后两者要相乘，所以把后面的i换为j，然后代入L。（下面每对x都隐藏了第一个x的转置符号）

\[L = \frac{1}{2}(\sum_{i}\sum_{j}\lambda^{(i)}\lambda^{(j)}y^{(i)}y^{(j)}x^{(i)}x^{(j)})+\sum_i\lambda^{(i)}-\sum_{i}\sum_{j}\lambda^{(i)}\lambda^{(j)}y^{(i)}y^{(j)}x^{(i)}x^{(j)}+\sum_i\lambda^{(i)}y^{(i)}b \]

整理后已经没有了w和b了，那就只剩下求\(\lambda\)了

\[\max_{\lambda_i} L= \sum_i\lambda^{(i)} - \frac{1}{2}(\sum_{i}\sum_{j}\lambda^{(i)}\lambda^{(j)}y^{(i)}y^{(j)}x^{(i)}x^{(j)})\\ s.t. \ \ \lambda \ge0\ \ \ ,\sum \lambda^{(i)}y^{(i)}=0 \]

最终的解答就不能再计算下去了，一般通过固定\(\lambda\)，剩下一些做调整，找到一个梯度最小的组合后，在固定其他，不断重复。

由上面的（1）的函数可知，当模型估计正确时，\(\lambda=0\)才能使L最小化，所以只有刚好在边界上的点的\(\lambda\)才大于0，只有这些点才会影响边界的形成。它们也被称为support vectors。

这里计算的关键在于对偶的\(⟨x^{(i)},x^{(j)}⟩\)，归纳为K函数，即kernel function，一个量化两个observation相似程度的函数。上面的kernel是线性的，也可以改用其他形式的kernel。当support vector classifier 采用其他非线形kernel时，称为SVM。例如radial kernel（rbf）根据附近的observation划分，需要调节gamma，越大越flexible

由于此方法在分界上过度敏感，且有时数据不是完全可分的，所以会减弱一些约束，变为soft margin。

\[s.t.\ \ y^{(i)}(w^\top x^{(i)}+b)\ge1-\epsilon_i \ \ , \ \ \epsilon_i \ge0\ \ , \ \ \sum_{i=1}^n \epsilon_i \leq C \]

此时允许observation落在错误的一侧（超过margin）。 判断大于等于1是正确划分，小于1大于0是在margin里错误的一边，小于0就是在margin外错误的一边。C代表对这些错误的总量限制。

此方法中的support vectors是边界上以及错误地超越边界的observation。

SVM和LR是类似的，只是最小化函数和限制函数调转了。总的来说，SVM在 well-separated classes时表现更好，重叠多时后者更好。

EM

Bernoulli混合模型

例子：有A，B，C三枚银币，各自出现正面的概率是\(\pi​\)， p， q。实验室先抛A，如果正面则抛B，然后用B的结果确定y。反之背面抛C，C结果作为y。问P(Y|\(\theta​\))。（\(\theta​\)表示上面三个参数）

设置隐藏参数Z表示抛A的结果，所以\(P(y|\theta)=P(y, Z|\theta)=\sum_zP(y|z,\theta)P(z|\theta)\)

第一部分：\(\sum_ZP(y|Z,\theta)=P(y|Z=0,\theta)+P(y|Z=1,\theta)=q^y(1-q)^{1-y}+p^y(1-p)^{1-y}​\)

第二部分：\(P(Z=1|\theta)=\pi\ , \ P(Z=0|\theta)=1-\pi​\)

得出：\(P(y|\theta)=p^y(1-p)^{1-y}\pi+q^y(1-q)^{1-y}(1-\pi)\)。这就是Bernoulli混合模型，当然也可以换成其他混合模型，如GMM。

根据极大似然估计：\(P(Y|\theta)=\prod_{i=1}^NP(y|\theta)=\sum_{i=1}^NlogP(y|\theta)\)

如何估计\(\theta​\)？可以搜索不同的参数值，直到似然值最大，也可利用迭代更新的方法，即下面的EM算法。

设置一个\(\mu\)表示当前y的结果有多大概率是抛B得到的，或者说当前y的结果有多大概率是在A抛出正面，Z=1，的情况后得到的。

\(\mu_{m+1}=p_m^y(1-p_m)^{1-y}\pi_m / P(y|\theta_m)​\) ，其中，原三个参数的初始值可随机设置。

\(\pi_{m+1}=\frac{1}{N}\sum_{i=1}^{N}\mu_{m+1}\)，利用\(\mu\)估计当前样本出现B的个数（这个个数是非整的）然后除以N得概率，即\(\pi\)的值

\(p_{m+1}=(\sum_{i=1}^{N}y\mu_{m+1})/(\sum_{i=1}^{N}\mu_{m+1})​\)，被估计为B的部分中，出现正面的概率是多少。

\(q_{m+1}=(\sum_{i=1}^{N}y(1-\mu_{m+1}))/(\sum_{i=1}^{N}(1-\mu_{m+1}))\)

EM算法

Jensen's inequality：𝐸[𝑓(𝑥)] ⩾ 𝑓(𝐸[𝑥]) if f() is a convex function; 𝑓(𝐸[𝑥]) ⩾ 𝐸[𝑓(𝑥)] if f() is a concave function.

根据极大似然函数\(P(Y|\theta)=\sum_{i=1}^NlogP(y|\theta)\)，加入隐藏变量z可得

\[\sum_{i=1}^Nlog\sum_zP(y, z|\theta)\\ = \sum_{i=1}^Nlog\sum_zQ_i(z)\frac{P(y, z|\theta)}{Q_i(z)}\ \ \ (此处Q_i是z的概率分布)\\ \ge\sum_{i=1}^N\sum_zQ_i(z)log\frac{P(y, z|\theta)}{Q_i(z)}\ \ \ (𝑙𝑜𝑔 𝐸[𝑥] ⩾ 𝐸[𝑙𝑜𝑔(𝑥)]) \]

上面有了概率分布、累加和分数部分相当于f(z)，那么就能构造出期望，从而使用Jensen不等式。接下来是最大化下限，即\(Q_iz\)取什么值时结果才是最大？回顾决策树的信息论中，各种z出现概率相等时熵最大。此处的\(\sum_zQ_i(z)log\frac{P(y, z|\theta)}{Q_i(z)}\)就相当于E(H(z))。所以\(P(y, z|\theta)/Q_i(z)=c\)时最大，而\(\sum_zQ_i(z)=1\)，所以可以作为c，那么可以计算出\(Q_i(z)=p(z|x,\theta)\)，这就对应上面例子中的\(\mu\)了。此时EM算法也就推断完了：

E-step：利用M-step的\(\theta\)计算\(Q_i(z)\)；M-step：利用E-step的\(Q_i(z)\)更新\(\theta\)，从而最大化极大似然函数。

HMM动态混合模型

如果上面硬币问题中B和C不是由A确定，而是由之前抛的硬币决定，那么就成了动态混合模型。即一开始有个概率\(\pi\)决定用B还是C来抛，当选择用B，那么下一次有一定概率还是用B，有另一个概率用C，反之亦然，所以这里就有4个转移概率，用A表示。而B和C又分别有不同的概率抛出正面，所以有4个释放概率，用B表示。在HMM场景下，Q是隐藏变量，即背后使用了B还是C并不知道，只知道它们的选择存在概率A，我们能观察的只有y。

\[P(y|\theta)=P(y|A,B,\pi)\\ P(Y,q)=P(q_0)\prod_{t=0}^{T-1}P(q_{t+1}|q_{t})\prod_{t=0}^{T}P(y_{t}|q_{t})\\ =\pi\prod_{t=0}^{T-1}A_{q_{t}->q_{t+1}}\prod_{t=0}^{T}B_{q_{t}->y_{t}}A表示状态转移概率，B表示释放概率。\\ P(y)=\sum_q P(Y,q)=\sum_{q_0}\sum_{q_1}...\sum_{q_T}P(Y,q)\ \ \ 实际上就是T个状态中B和C的全排组合的概率和 \]

全排序计算比较繁琐，可以用前向后向求解（未完善）

\[\alpha(q_{t+1})=\sum_{q_t}\alpha(q_t)A_{q_{t}->q_{t+1}}B_{q_{t}->y_{t}}\\ P(y)=\sum_j \alpha(q_T=j) \ \ j表示状态的种类 \]

另外也可以利用EM算法求解（Baum-Welch算法）

\[Q(\theta, \theta_t)=E[log\pi_{q_0}]+E[\sum_{t=1}^{T}log A_{q_{t}->q_{t+1}}] + E[\sum_{t=1}^{T}log B_{q_{t}->y_{t}}] \]

上面是E-step，对上面三个部分分别进行求解可以得到M-step中的\(\theta \ \epsilon \ (\pi, A,B)\)

Topic Model

Probabilistic latent semantic analysis (PLSA), is a statistical technique for the analysis of two-mode and co-occurrence data.

\[P(w|\theta)=\sum_d\sum_cP(w|c)P(c|d)P(d|\alpha) \]

d是文档索引变量，c是从文档的主题分布P(c | d)中提取的主题，w是从该主题的单词分布P(w | c)中提取的单词。

\(\alpha\)由Dirichlet distribution获得，其函数为\(f(x_1,...,x_k;\alpha_1,...,\alpha_k)\)，输入k个\(\alpha\)能够采样出一个k维的向量x，而且这k个\(x_i\)之和为1，所以相当于产生了一个PMF。所以可以通过Dirichlet distribution产生一个文档的主题分布。

Latent Dirichlet allocation (LDA) is a hierarchical generative statistical model。 模型假定文档是少量主题的混合，而这些文档主题会产生文档中的单词。单词作为observations，分别由相应的主题分布产生。简单来说，每个主题都是一个单词集的分布，文档可以表示为这些主题分布的混合题。

Topic Model

在LDA基础上再进一步，认为w也是由一个分布\(\phi\)产生，类似于词典，所以维度极大。而这个分布由\(\beta\)通过Dirichlet distribution产生。

通过对大量文档的学习，模型就能推断出潜在的主题分布，进而对文档进行分析，计算出不同文档之间的相似度。

Unsupervised Learning

K-Means

目标：同类的variation尽量小

\[\mathop{maximise} \limits_{C_1 ,...,C_k} ^{}\left\{\sum_{k=1}^{K} W(C_k) \right\} \]

Ck表示第k个cluster，W(.)表示衡量variation的函数，具体实现有很多，例如L2。

K-Means的一个问题是需要预先设置K的个数，而hierarchical clustering可以后来再设K。

hierarchical clustering

相似度根据两个observations交汇点的高度，越高越不相似。下左图，(2，8，5，7）与（9）的交汇高度是一样的。

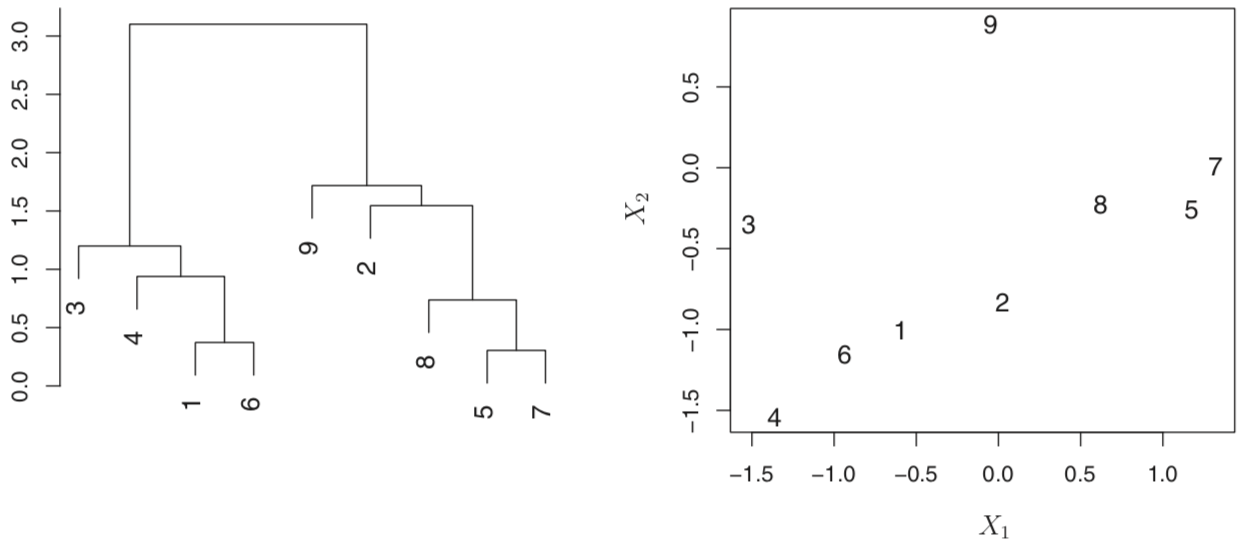
分类就看从哪个高度水平切开，得出多少树枝就多少类。例如上左以2.0进行分割，那就两类。

实现的过程：一开始n个clusters，然后组合最接近的两个observation/cluster得到n-1个cluster，然后不断重复。判断两个cluster接近程度的方法有：complete，average，single和centroid，前两者最受欢迎，因结果树更加平衡。

这个方法的问题出现在这么一个场景：在一组数据中，如果分成两组的最优解是男/女，而分成三组的最优解是国籍（三个国家）。这个方法分三组的最优方法会是在男/女的基础上把男或女的组进行拆分。在这种情况下，它分类的“准确性”比KMeans差。

针对K-Means和hierarchical clustering

Dissimilarity Measure 的选择：距离或者关系。例如按距离来分，会把购买量类似的顾客分为一类；按关系来分，会把购买种类类似的顾客分为一类。

对于数据的scale取决于应用的场景。

上面两个方法的问题：会对一些outliers强行分类。

Dimensionality Reduction

作用：save time and memory, remove noisy and redundancy，但模型效果一般会下降。

实现方法：Eliminating low variance coordinates

特征向量与特征值：\(Mu=\lambda u\)，其中M为d x d矩阵，u是d维特征向量，\(\lambda\)为特征值。针对一个矩阵求其特征值和特征向量，就是求解特征方程\(|\lambda E-A|=0\)。对称矩阵有d个特征向量，特征向量之间相互垂直。

PCA

transform an 𝑁 × 𝑑 matrix 𝑋 into an 𝑁 × 𝑚 matrix 𝑌

步骤：

  • Centralized the data (subtract the mean).
  • Calculate the 𝑑 × 𝑑 covariance matrix.
  • Calculate the eigenvectors of the covariance matrix (orthonormal).
  • Select m eigenvectors that correspond to the largest m eigenvalues to be the new basis.

PCA提取出方差最大的前k个特征向量，把原数据对这些坐标进行投影。

SVD

奇异分解（SVD，特征分解的拓展不再限定为方阵）：\(A_{m * n}=U_{m * m}Σ_{m * n} V^\top_{n*n}\)，其中U由左奇异向量组成，Σ是一个对角阵，每一个对角线上的元素就是一个奇异值，而且值从大到小排序，V为右奇异。奇异值与特征值类似，同样可以选取最大的几个来达到降维的目的。

对\(A^\top A\)进行特征分解得出\(\lambda\)，\(\lambda\)开根号就是奇异值。

LLE

LLE的目标是将高维度上的线性关系保留到底维度上。下面\(x^{(j)}\)表示\(x^{(i)}\)周围的J个点之一。

\[\min \varepsilon^{(i)}=|x^{(i)}-\sum_jw^{(j)}x^{(j)}|^2\ \ \ where:\sum_jw^{(j)}=1\\ =|\sum_j(x^{(i)}-x^{(j)})*w^{(j)}|^2\\ =|XW|^2\\ =W^\top X^\top XW \]

利用拉格朗日函数求解出w

\[L = W^\top X^\top XW + \lambda(1-I^\top W)\\ \frac{\partial L}{\partial W}=0 =>2X^\top XW-\lambda I=0=>W=\frac{\lambda}{2}(X^\top X)^{-1}I\\ \frac{\partial L}{\partial \lambda}=0 =>I^\top W=1 \]

然后将w代入下面函数

\[C(y)=\sum_i|y_i-\sum_jw^{(j)}y^{(j)}|^2\\ where\ \ \sum_iy^{(i)}=0\ \ and\ \ y^\top y/N=I \]

最后解出

\[(1-w)^\top(1-w)y=-\lambda y/2 =>My=\mu y \]

即可以求M的特征值和特征向量，进而把x压缩为y。由于w的作用，高维度x的线性关系在底维度的y依然存在。

T-SNE

在LLE的基础上，从J个周围点到考虑所有点，变为SNE。但SNE的降维对不同的点是不对称的，而且会导致数据拥挤，所以最后用t分布代替正态分布变为T-SNE。这是目前非线性降维中比较先进的方法。

posted @ 2019-01-19 22:50  justcodeit  阅读(802)  评论(0)  编辑  收藏  举报