物理模拟
基本概念、质点弹簧系统、运动学、求解常微分方程、刚体与流体
质点弹簧系统
现在我们模拟一个弹簧系统。
首先弹簧：
但是这样的话，没有能量损失，弹簧就会一直运动下去。所以增添摩擦力。
符号定义：
这样的问题是，摩擦力和速度方向相关，比如b围绕a转？
所以，摩擦力发生在弹簧内部，也就是说：
质点弹簧可以组合成多种结构。
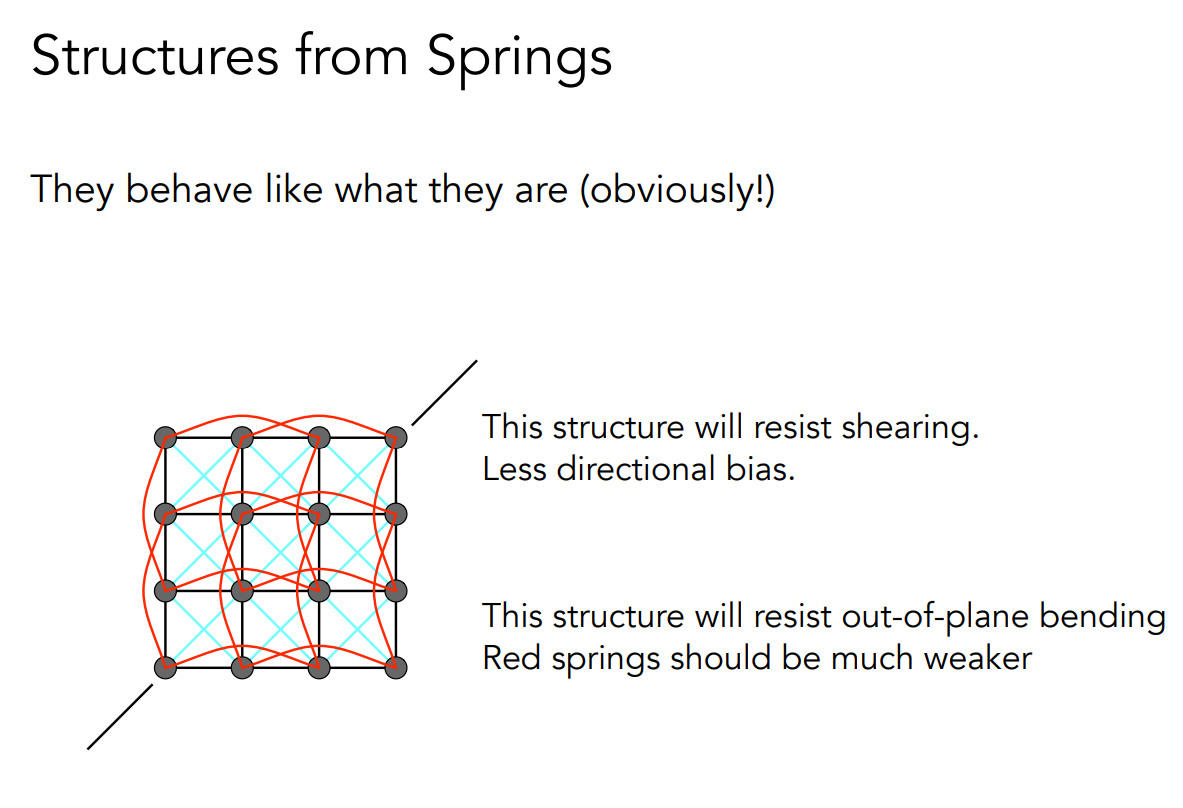
想象模拟一个布料，来建立质点弹簧质点之间的关系。
对抗沿着角拉开的力，增加了蓝色线。对抗对折的力，增加了A-B，AB中间间隔一个的红色线。但是布料是可以被对折的，所以红色线很微弱。
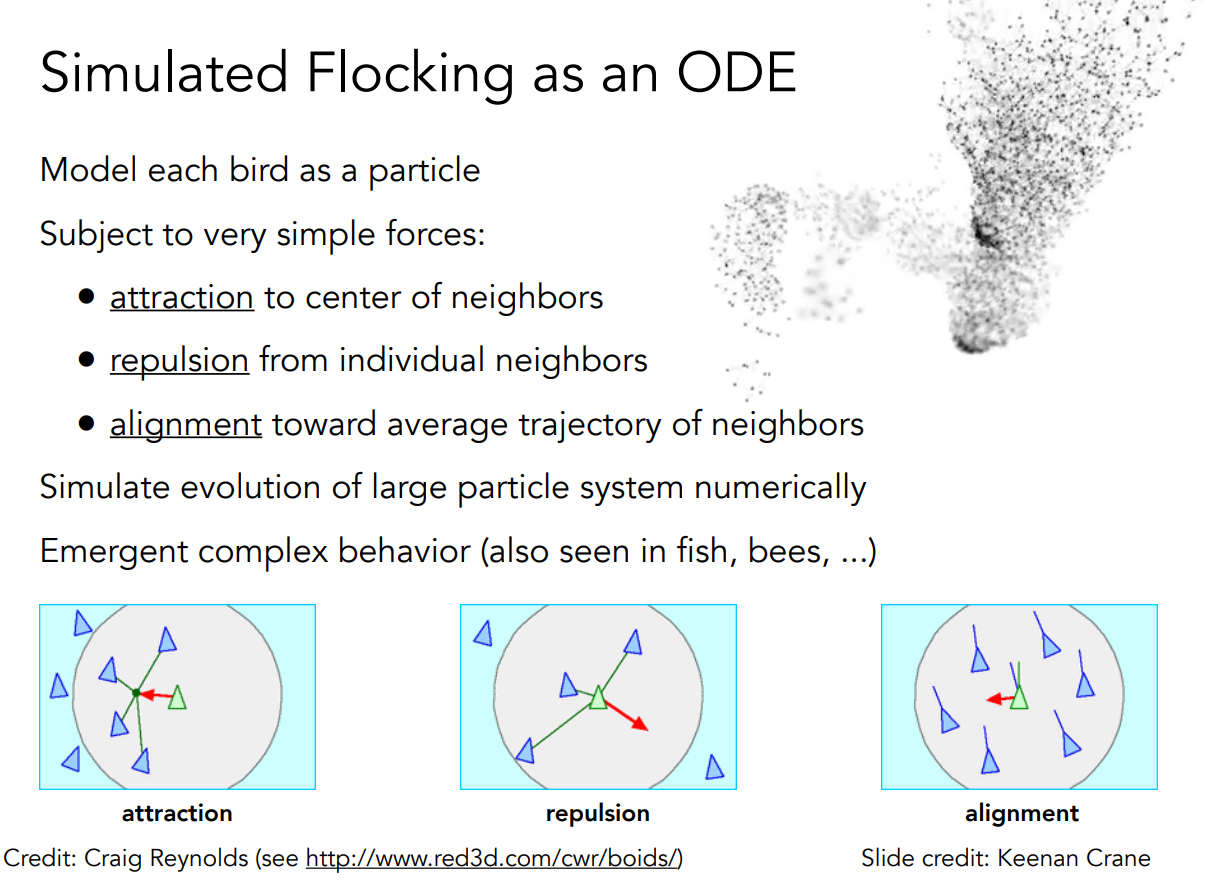
粒子系统
粒子系统包含大量粒子。每一个粒子的运动被一个集合的力所定义。
对一个新的帧来说：
- 创建粒子
- 计算每一个粒子上的力
- 更新每一个粒子的位置和速度
- 移除粒子
- 渲染粒子
常见粒子系统的力
速度场
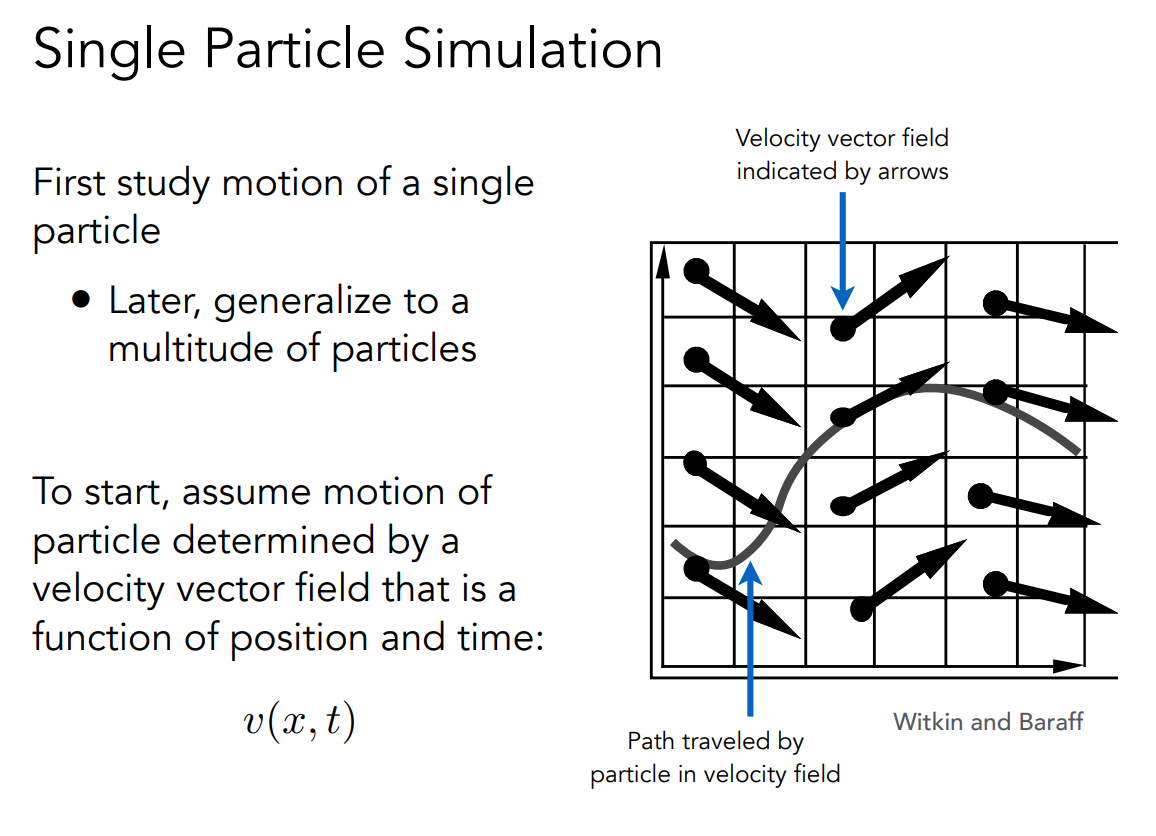
定义一个位置和时间，可以得到这个点下速度。
可以列出方程：
但是因为根据采样\(\delta t\)不同，得到的最终位置也不同。但是最终都会偏离，因为\(\delta t\)还是会有一个积累误差在里面。
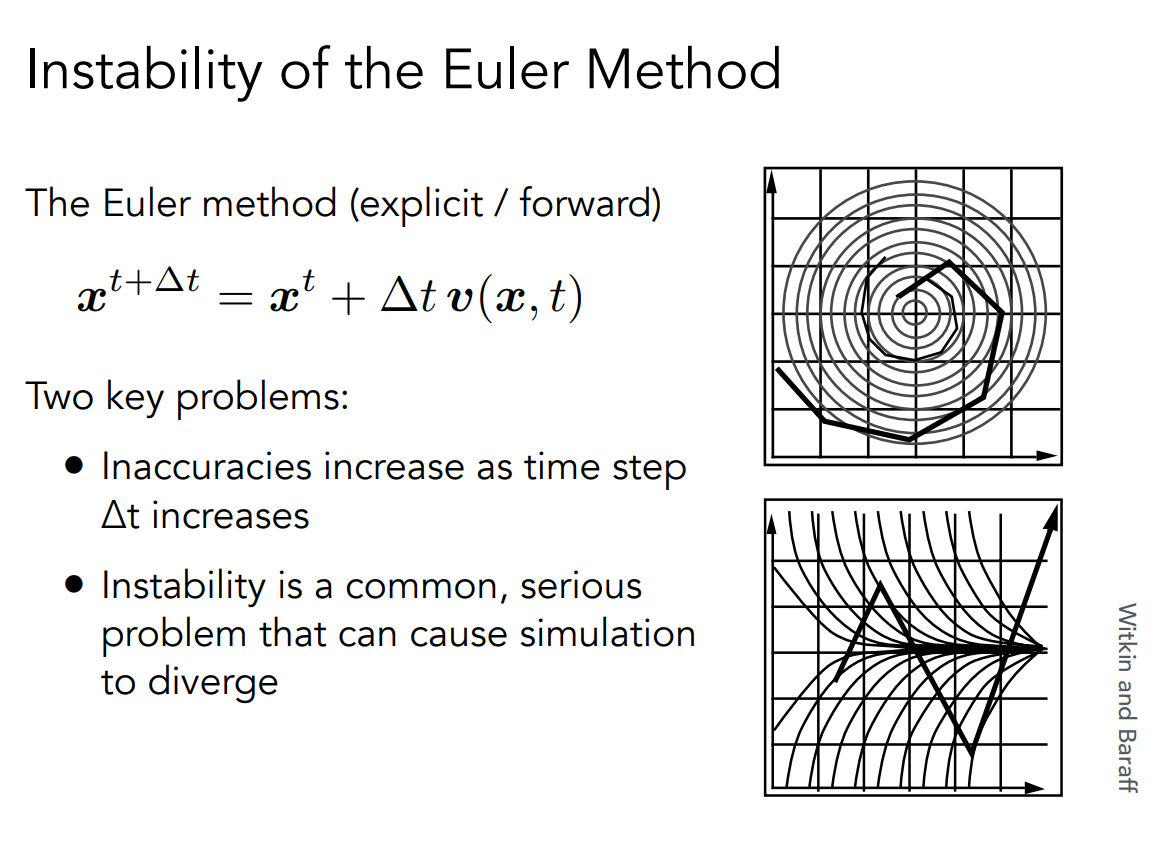
这里有一些方法减少不确定度：
- 中点法
- 自适应步长法
- 隐式方法（使用下一时刻的速度）
- 基于位置的方法（不考虑运动了，我只考虑位置）
中点法
中点法误差小的原因，多展开了一项（感觉有点像泰勒展开）：
自适应步长
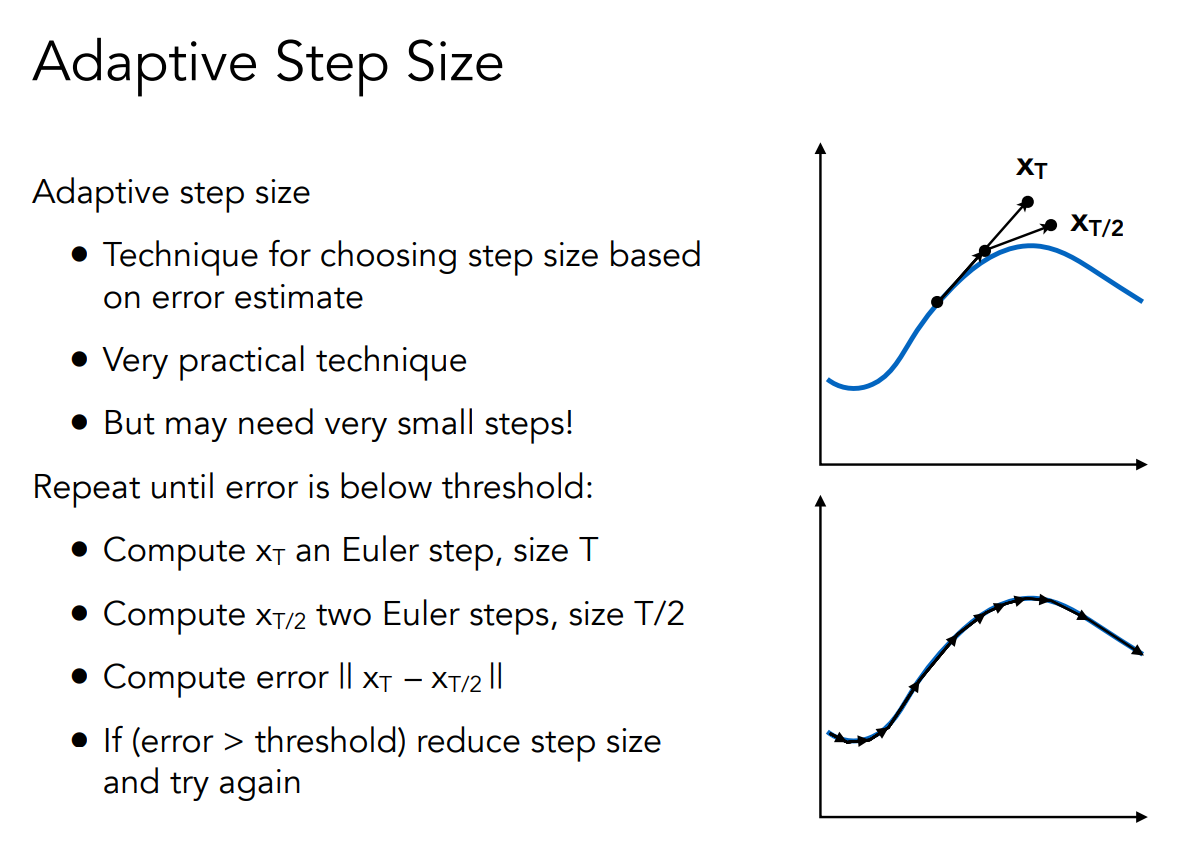
- 计算\(x_{T/2}\)，直到\(X_T\)和\(X_{T/2}\)的差别大过阈值。【这里很奇怪，也可能到最后都大不过阈值，应该再设置一个出口】
隐式
是一种叫RK的算法
Position-Based / Verlet Integration
不使用对速度的约束了，直接使用对位置的约束。很快很简单，但是可能不符合能量损失函数。
将水模拟为刚体小球的运动。定义与粒子位置相关的密度（density）误差，然后使用梯度下降法优化。
质点和网格法
质点法以每一个质点为关注点，网格法可以认为以固定的网格流水的质点。
运动学
前向运动学
常见的运动学结构
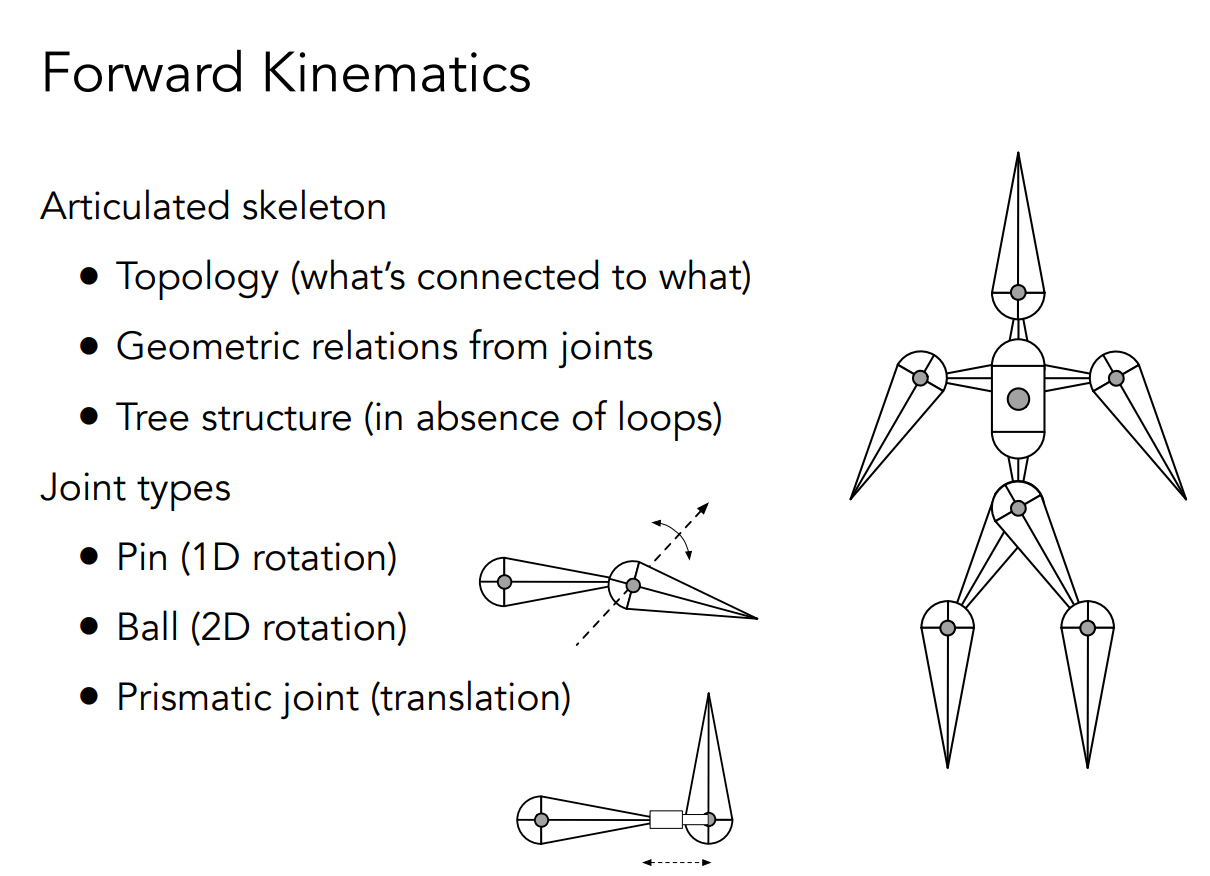
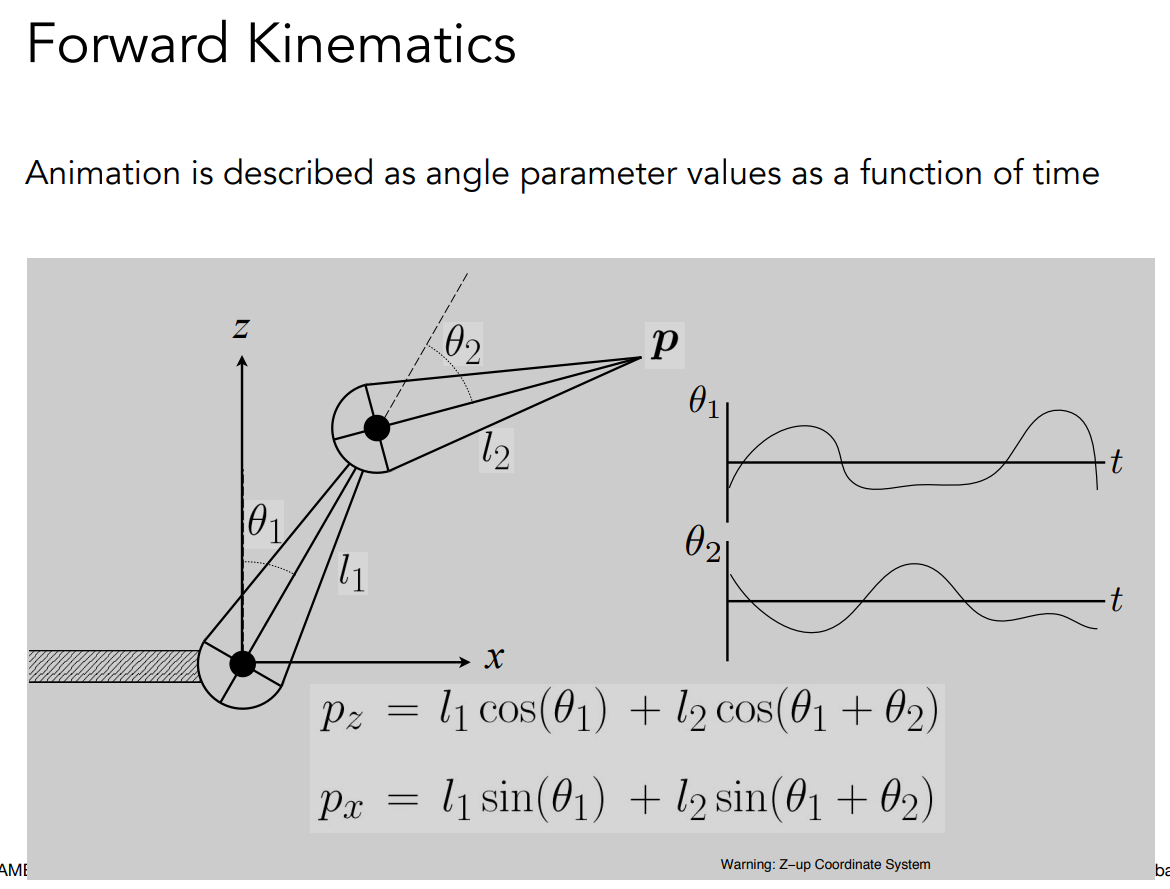
前向运动学指的是给定每一关节的运动角度然后就可以计算出位置。
逆向运动学
根据位置求解每个关节之间的运动角度。这样的话可能会有多解和不存在解的现象。
求解的过程是一个很适合用机器学习做优化的过程。选一个初始点、定义误差、计算优化方向、沿着优化方向做优化。
