相机姿态估计
总目标:计算相机运动
2D-2D:对极几何
对极约束
\[x{_2}{^T} t^∧Rx_1=0
\]
\[p_2^TK^{-T}t^∧RK^{-1}p_1=0
\]
它的几何意义是\(O_1,P,O_2\)三者共面。对极约束中包含了平移和旋转。
定义基础矩阵(Fundamental Matrix)\(F\)和本质矩阵(Essential Matrix)\(E\),
\[E=t^∧R,F=K^{-T}EK^{-1}
\]
则对极约束:
\[x_2^TEx_1=p_2^TFp_1=0
\]
本质矩阵E的求解
E的性质:
- 对极约束是等式为零的约束,E乘以任意非零常数后,对极约束依然满足
- \(E=t^∧R\),其奇异值是\([\sigma ,\sigma ,0]^T\)的形式。
- R和t共有六个自由度,则E也有6自由度。但由于尺度等价性(可以同时乘以常数),E实际上有5个自由度。
八点法
- 为什么选择八个点,而不是5个点?
E的内在性质是一种非线性性质,在估计时会带来麻烦,因此,也可以只考虑它的尺度等价性。E是一个3✖3的矩阵,9个点,考虑尺度等价性后,需要8个点。 - 多于8对点的情况:
计算最小二乘解,将八点法中的左侧矩阵记为A:
Ae=0,八点法中A的大小为8✖9,若给定的匹配点多于8,构成超定方程,则不一定能求得e。因此可以最小化一个二次型来求解:
\[min_e||Ae||^2_2=min_ee^TA^TAe
\]
- 八点法:
- 选取8对匹配点,代入对极约束。则可求得E。
- 再利用SVD分解:\[E=U\Sigma V^T \]
- 求得t,R的可能值:
\[t_1^∧=UR_Z(\frac{\pi}{2})\Sigma U^T,R_1=UR_Z^T(\frac{pi}{2})V^T \]\[t_2^∧=UR_Z(-\frac{\pi}{2})\Sigma U^T,R_2=UR_Z^T(-\frac{\pi}{2})V^T \]- \(R_Z(\frac{\pi}{2})\)表示沿z轴旋转90度得到旋转矩阵。同时E和-E等价,所以也可以对任意一个t取负号。因此,共存在4个解。但只有一个解使得P在两个相机中都具有正的深度。
- 我们根据线性方程求出的E可能不满足E的内在性质——奇异值可能不为\([\sigma ,\sigma ,0]^T\)的形式。因此,我们会刻意将\(\Sigma\)矩阵调整为上面的样子。\[E=U diag(\frac{\sigma_{1}+\sigma_{2}}{2},\frac{\sigma_{1}+\sigma_{2}}{2},0)V^T \]
单应矩阵H
- 通过假设场景中的特征点都落在同一平面上:\[-\frac{n^TP}{d}=1 \]得到每对匹配点的线性关系。然后选取8对点进行求解H。同样,再将H分解得到R和t。
- 单应性的重要意义:
当特征点共面或者发生相机纯旋转时,基础矩阵的自由度下降,这就出现了退化(degenerate)。此时,基础矩阵多余出来的自由度将会主要由噪声决定。
为此,我们会同时估计基础矩阵F和单应矩阵H,选择重投影误差比较小的那个作为最终的运动估计。
三角测量
目的是求出深度。
\[s_2x_2=s_1Rx_1+t
\]
同乘\(x_2^∧\):
\[s_2x_2^∧x_2=s_1x_2^∧Rx_1+x_2^∧t
\]
\[s_2x_2^∧x_2=0
\]
变为求解$$s_1x_2^∧ Rx_1+x_2^∧t=0$$
3D-2D:Pnp
DLT
每对匹配点满足
\[t_1^Tp-t_3^Tpu_1=0\\
t_1^Tp-t_3^Tpu_1=0\]
找出6对匹配点,列12个方程求解t(定义[R|t]为一个3✖4的矩阵,\(t_1\)代表\((t_1,t_2,t_3,t_4)^T\),以此类推),但旋转矩阵需要满足约束,可以由QR分解来求得。
P3P
通过余弦定理,选择3对匹配点进行运算。
最小化重投影误差(Bundle Adjustment)
Bundle Adjustment:把相机和三维点放在一起进行最小化的问题。
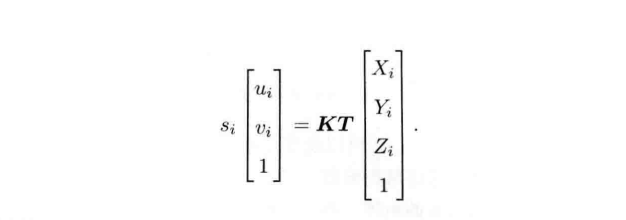
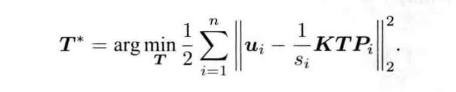
其中\(u_i\)表示观测数据,当e为像素坐标误差,x为相机位姿。
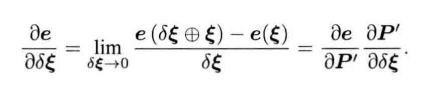
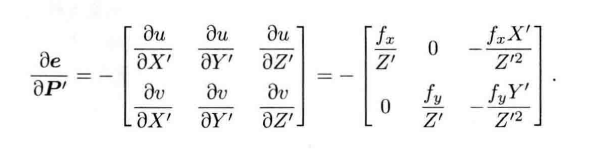
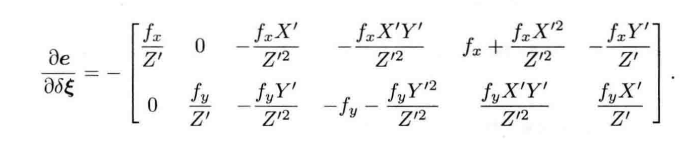
3D-3D:ICP(Iterative Cloest Point)
ICP可以分为以下三个步骤求解:
- 计算两组点的质心位置\(p,p^{'}\),然后计算每个点的去质心坐标:
\[q_i=p_i-p,q^{'}_i=p^{'}_i-p^{'}
\]
- 根据以下优化问题计算旋转矩阵:
\[R^* = argmin_R\frac{1}{2} \sum_{i=1}^{n} \lvert \rvert q_i - R q^{'}_{i} \lvert \rvert ^2
\]
- 根据第2步的R计算t:
\[t^*=p-Rp^{'}
\]
SVD求解
定义\(W=\sum_{i=1}^{n} q_iq^{'T}_i\).
W是一个3✖3的矩阵,对W进行SVD分解:
\[W=U\Sigma V^T
\]
当W满秩时,R为
\[R=UV^T
\]
非线性优化方法
以李代数表达位姿时,目标函数可以写成:
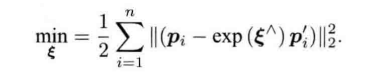
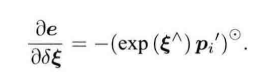


 浙公网安备 33010602011771号
浙公网安备 33010602011771号