第八章 （一）分治 练习题
练习题一：最大连续和问题：长度为n的序列，求最大连续和。
1 /**
2 * 最大连续和问题：长度为n的序列，求最大连续和。
3 * 枚举解法
4 * 时间复杂度O(n^3)
5 * @param a
6 */
7 public static int test1(int[] a) {
8 int max=a[0];
9 for(int i=0;i<a.length;i++) {
10 for(int j=i;j<a.length;j++) {
11 int sum=0;
12 for(int m=i;m<=j;m++) {//求[i,j]的和
13 sum+=a[m];
14 }
15 if(sum>max)max=sum;
16 }
17 }
18 return max;
19 }
20 /**
21 * 最大连续和问题：长度为n的序列，求最大连续和。
22 * S[i]表示a[0]+...+a[i]则S[j]-S[i-1]表示[i，j]的和
23 * 时间复杂度：O(n^2)
24 * @param a
25 */
26 public static int test2(int[] a) {
27 //求S[i]
28 int[] s=new int[a.length];
29 s[0]=a[0];
30 for(int i=1;i<a.length;i++) {
31 s[i]=s[i-1]+a[i];
32 }
33 int max=s[0];
34 for(int i=1;i<a.length;i++) {
35 for(int j=i;j<a.length;j++) {
36 if(s[j]-s[i-1]>max)
37 max=s[j]-s[i-1];
38 }
39 }
40 return max;
41 }
42 /**
43 * 最大连续和问题：长度为n的序列，求最大连续和。
44 * 对test2的优化，s[j]-s[i-1]对于确定的j，s[i-1]越小结果越大，记录当前出现的最小值
45 * 时间复杂度O(n)
46 * @param a
47 */
48 public static int test3(int[] a) {
49 //求S[i]
50 int[] s=new int[a.length];
51 s[0]=a[0];
52 for(int i=1;i<a.length;i++) {
53 s[i]=s[i-1]+a[i];
54 }
55 int min=s[0],max=s[0];
56 for(int i=1;i<a.length;i++) {
57 if(s[i]-min>max) max=s[i]-min;
58 if(s[i]<min) min=s[i];
59 }
60 return max;
61 }
62 /**
63 * 最大连续和问题：长度为n的序列，求最大连续和。
64 * 分治算法
65 * 时间复杂度O(nlogn)
66 * @return
67 */
68 public static int test4(int[] a,int x,int y) {
69 if(y-x==1) return a[x];//只剩一个元素，直接返回
70 //划分
71 int m=x+(y-x)/2;
72 int maxs=Math.max(test4(a,x,m), test4(a,m,y));//[x,m) [m,y)
73 int v=0,L,R;
74 //从m向右
75 L=a[m];
76 for(int i=m;i<y;i++) {
77 L=Math.max(L, v+=a[i]);
78 }
79 //从m-1向左
80 v=0;R=a[m-1];
81 for(int i=m-1;i>=x;i--) {
82 R=Math.max(R, v+=a[i]);
83 }
84 return Math.max(maxs, L+R);
85 }
可以看到本问题的分治法解法，将对数组求最大连续和的问题划分为求[x,m)[m,y)的最大值，以及在[x,y)之间的连续最大值的起点和终点（所以它算法是以m为划分点向两边扩散开，最后把L+R合并），这三个子问题，逐步求解
DP解法：
/**
* 求解最大子段和
*/
public static void test(int[] a) {
int[] b=new int[a.length];//从i到n最大的最大和
//b[i]=max(a[i],b[i+1]+a[i])
b[a.length-1]=a[a.length-1];
int maxsum=Math.max(b[a.length-1], 0);
for(int i=a.length-2;i>=0;i--) {
if(b[i+1]>0)
b[i]=b[i+1]+a[i];
else
b[i]=a[i];
if(b[i]>maxsum) {
maxsum=b[i];
}
}
}
进行空间优化，观察可知b数组只用到了b[i+1]，所以只需保存b[i+1]即可，但是这样最优解就会变得难求
/**
* 求解最大子段和
*/
public static void test(int[] a) {
int b=a[a.length-1];
int maxsum=Math.max(b, 0);
for(int i=a.length-2;i>=0;i--) {
if(b>0)
b=b+a[i];
else
b=a[i];
if(b>maxsum) {
maxsum=b;
}
}
}
练习题二：排序和搜索
合并排序（求逆序对数）
快速排序（求从小到大第k个数）
二分查找
练习题三：大整数乘法
设X和Y都是n位二进制数现在要计算他们的乘积XY。
按正常的乘法规则要做n2次一位数的乘法，计算步骤太多。下面用分治法来解决此问题：
将n位的二进制整数X和Y各分为2段，每段的长为n/2位(为简单起见，假设n是2的幂)，如图所示。
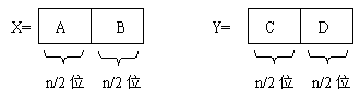
由此，X=A2n/2+B ，Y=C2n/2+D。（计组里面乘法的原理）这样，X和Y的乘积为：
XY=(A2n/2+B)(C2n/2+D)=AC2n+(AD+CB)2n/2+BD (1)
计算时间复杂度:
T(1)=1
T(n)=4T(n/2)+O(n)
解得T(n)=O(n2)。由此可见，仍需要n2次乘法
XY=AC2n+[(A-B)(D-C)+AC+BD]2n/2+BD (2)
虽然，式(2)看起来比式(1)复杂些，但它仅需做3次n/2位整数的乘法(AC，BD和(A-B)(D-C))，6次加、减法和2次移位。由此可得:
T(1)=1
T(n)=3T(n/2)+cn
其解为T(n)=O(nlog3)=O(n1.59)
可以看到如果要降低复杂度，在分成的规模一定时，减少子问题的个数，可以降低复杂度。用多次次要矛盾代替主要矛盾
练习题四：Strassen矩阵乘法
Strassen采用了类似于在大整数乘法中用过的分治技术，将计算2个n阶矩阵乘积所需的计算时间改进到O(nlog7)=O(n2.81)。
