第2章-分析复杂度来判断算法效率

目录

• 一、时间复杂度
  • 1. 求绝对值
  • 2. 数组求和
  • 3. 二分查找
  • 4. 冒泡排序
• 二、空间复杂度

算法复杂度用于分析算法运行所需计算机资源的量，需要的时间资源为时间复杂度，需要的空间资源为空间复杂度。

在判断一个算法的优劣时，可以抛开软件和硬件因素，只考虑问题的规模。编写程序前预先估计算法优劣，可以改进并选择更高效的算法。

一、时间复杂度

编程实现算法后，算法就是由一组语句构成，算法的执行效率就由各语句执行的次数所决定。一个算法花费的时间与算法中语句的执行次数成正比，把时间复杂度记为 \(T(n)\) ，一般情况下，算法的基本操作重复执行的次数是关于模块 \(n\) 的一个函数 \(f(n)\)，因此，可以把算法的时间复杂度记做：\(T(n) = O(f(n))\)。

随着模块 \(n\) 的增大，算法执行的时间的增长率和 \(f(n)\) 的增长率成正比，所以 \(f(n)\) 越小，算法的时间复杂度越低，算法的效率越高。

研究复杂度的目的是要比较两个算法的效率的高低，并不需要仔细分析这个算法比那个算法多几次运算那么清，所以采用渐近复杂度分析来比较算法的效率。

在分析算法的时间复杂度时，一般都会规定各种输入情况得出最好情况下 \(T_{max}(n)\)、最坏情况下 \(T_{min}(n)\) 和平均情况下 \(T_{avg}(n)\) 。

1. 求绝对值

求一个整数的绝对值，代码如下：

public static int abs(int a) {
    return a < 0 ? -a : a;
}

该代码中只有一条运算指令语句，时间复杂度为 \(O(1)\)。

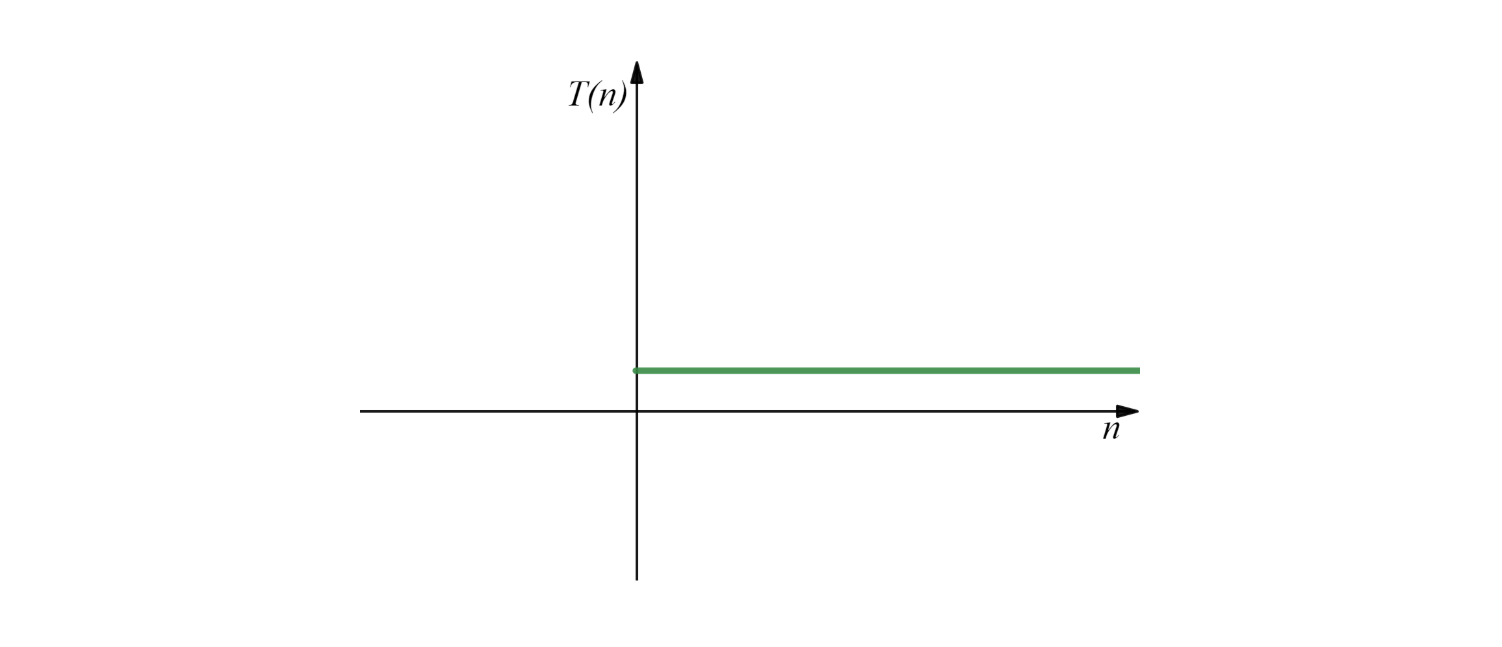
2. 数组求和

对数组内所有整数求和，代码如下：

public static int sum(int[] a) {
    int s = 0;
    for (int i : a) {
        s += i;
    }
    return s;
}

如果输入数组的大小为 \(n\) ，执行语句中初始化赋值需要时间 \(O(1)\)，循环语句中的赋值操作需要时间为 \(O(1)\times n\)，所以语句执行的时间为：

\[O(1)+O(1)\times n\approx O(n+1) \approx O(n) \]

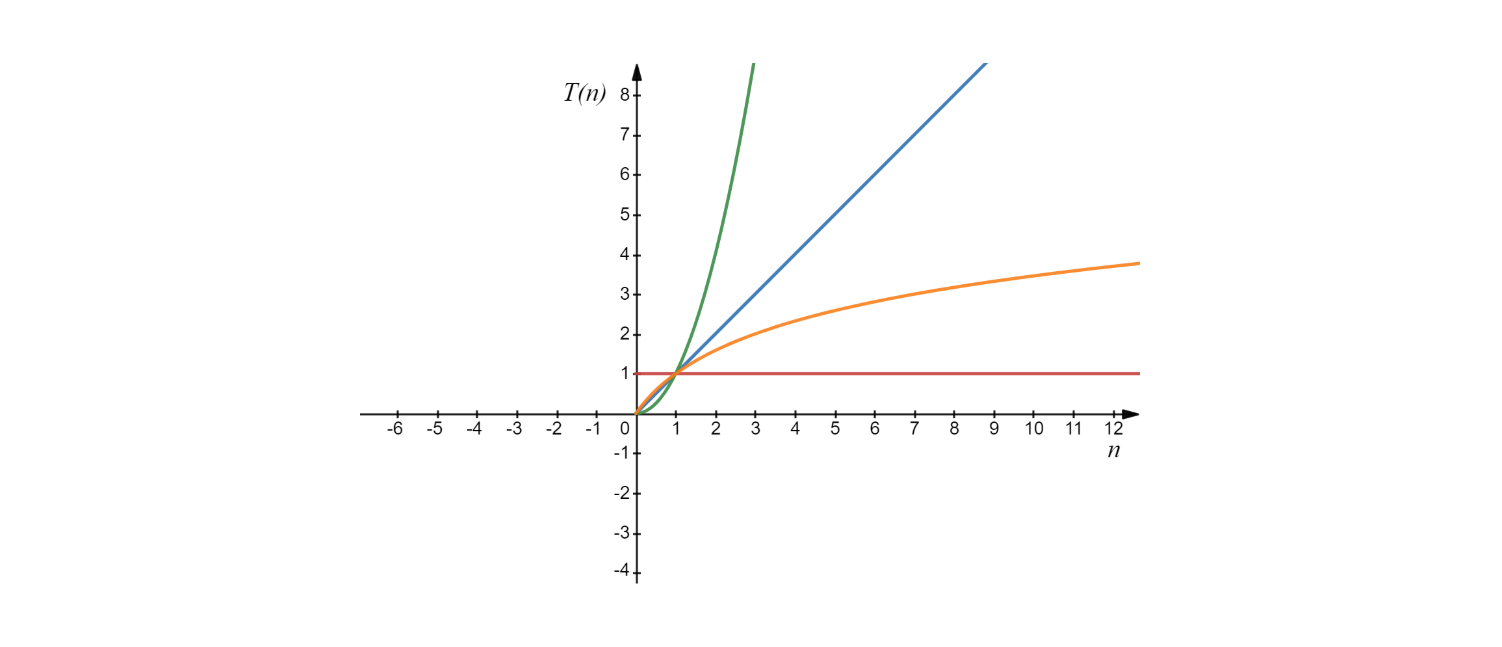
该时间复杂度随着规模大小趋势如下：

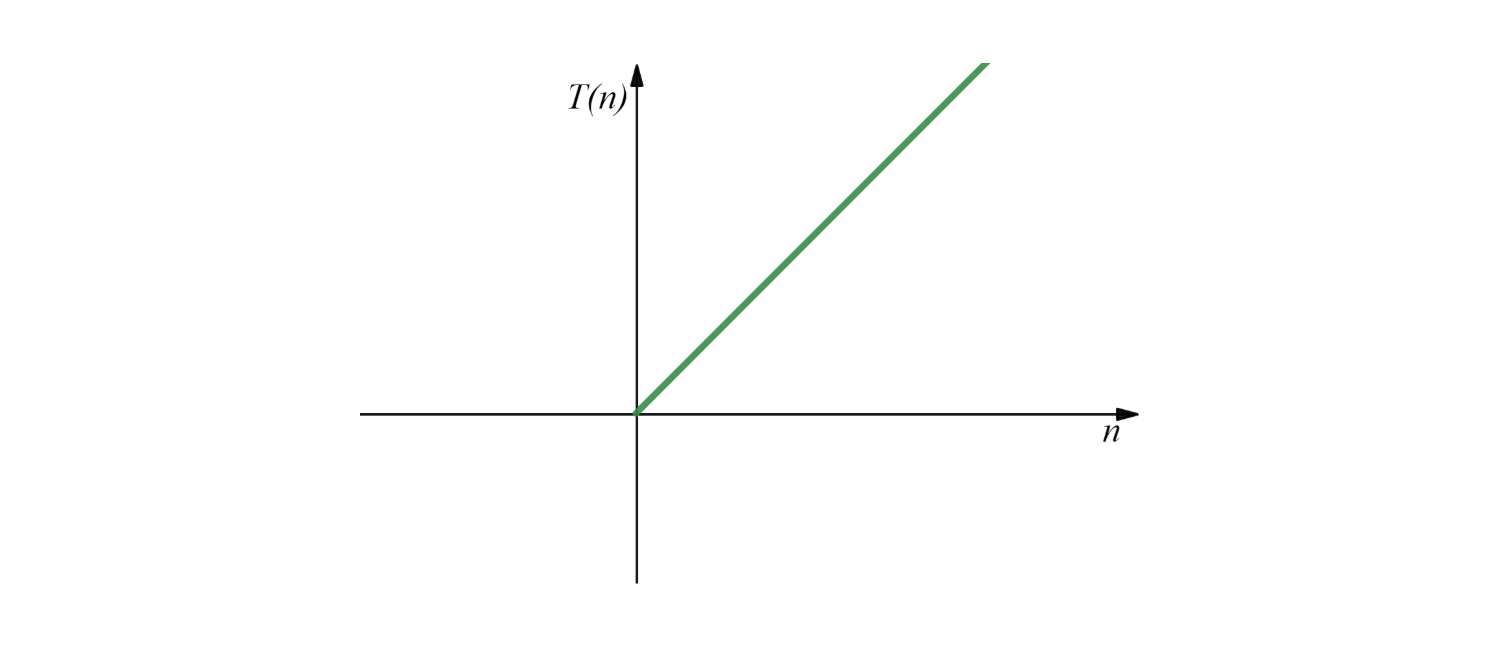
3. 二分查找

使用二分法在有序数组中找到某个元素的位置，代码如下：

public static int binarySearch(int[] a, int b) {
    int i, r = 0, l = a.length;
    while (r <= l) {
        i = (r + l) / 2;
        if (a[i] < b) {
            r = i + 1;
        } else if (a[i] > b) {
            l = i - 1;
        } else {
            return i;
        }
    }
    return -1;
}

假设这个循环执行了 \(k\) 次，每一次循环都会将规模 \(n\) 除以 2：

• 第 1 次，规模为 \(n\)；
• 第 2 次，规模为 \(\frac{n}{2}\)；
• 第 3 次，规模为 \(\frac{n}{4}\)；
• 第 \(k\) 次，规模为 \(\frac{n}{2^{k-1}}\) 。

当 \(n=1\) 的时候，查找结束，所以需要满足 \(\frac{n}{2^{k-1}}=1\)，简化后得 \(k=log_2n+1\approx log_2n\) ，所以二分查找的时间复杂度为 \(O(log\ n)\)。

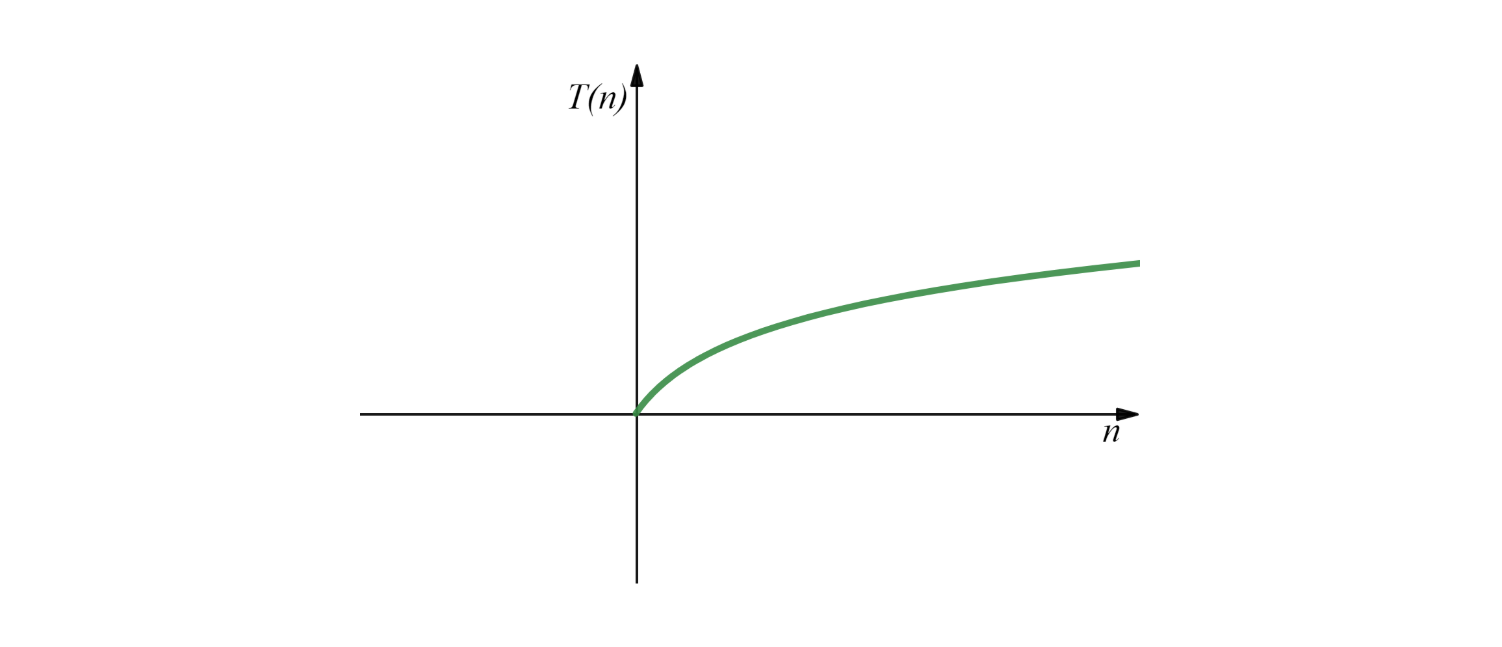
4. 冒泡排序

使用冒泡算法对整型数组进行排序，代码实现如下：

public static int[] bubbleSort(int[] a) {
    int temp;
    for (int i = 0; i < a.length - 1; i++) {
        for (int j = 0; j < a.length - 1 - i; j++) {
            if (a[j] > a[j + 1]) {
                temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
            }
        }
    }
    return a;
}

两层循环中比较的次数为 \((n-1)+(n-2)+(n-3)+...+1\) ，根据等差数列求和公式得出结果为 \(\frac{n(n-1)}{2}\)，忽略低次项，所以该算法的时间复杂度为 \(O(n^2)\)。

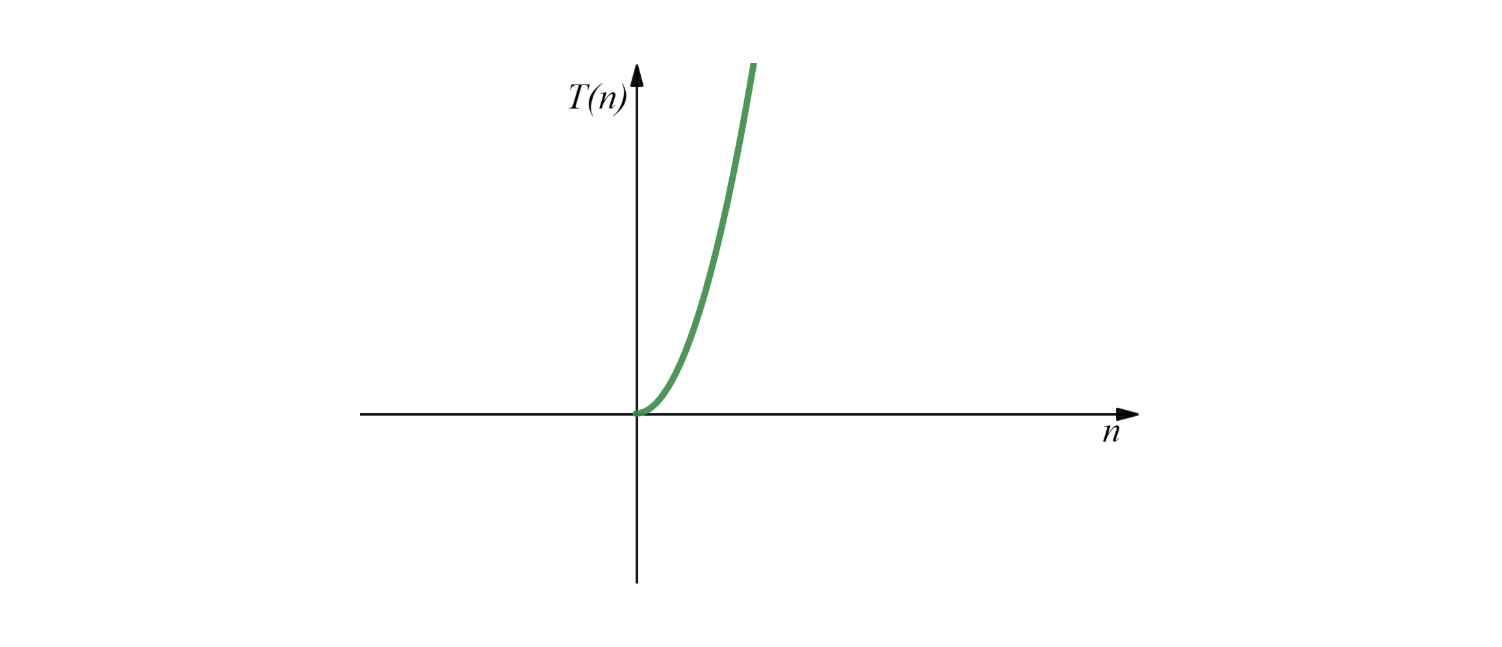
不是时间复杂越低的越好，要考虑数据规模，如果数据规模很小，甚至可以用 \(O(n^2)\) 的算法比 \(O(n)\) 的更合适。

二、空间复杂度

衡量算法性能的另一个重要方面，就是算法需要使用的存储空间量，即算法空间复杂度。我们希望对于同样的输入规模，在时间复杂度相同的前提下，算法所占的空间越少越好。

每次基本操作只会涉及到常数规模的空间，所以在分析和讨论算法时，只关注时间复杂度。当然，空间复杂度在对空间效率非常在乎的应用场景时，或者是问题的输入规模极为庞大时，也有其存在的意义。