动态DP小记

前言

矩阵乘法优化DP，重链剖分。

涉及到的知识点是比较复杂的，但是比较重要。

这是猫锟在 WC2018 讲的黑科技，一般用来解决树上的带有点权（边权）修改操作的 DP 问题，为了普及，甚至 CSP2022-S T4 考到了此知识点。

做法

这里以模板题 P4719【模板】"动态 DP"&动态树分治。

朴素DP

设 \(dp_{i,0}\) 表示不选 \(i\)，\(i\) 的子树的最大权独立集的权值大小。
\(dp_{i,1}\) 表示选 \(i\)，\(i\) 的子树的最大权独立集的权值大小。
则有：

\[\begin{cases} dp_{i,0}=\sum\limits_{x=1} \max(dp_{x,0},dp_{x,1})\\ dp_{i,1}=\sum\limits_{x=1} dp_{x,0}+a_i \end{cases} \]

最后答案 \(ans=\max(dp_{1,0},dp_{1,1})\)。

但显然，这个式子如果带修没法跑，复杂度会炸掉，要继续优化。

重链剖分

我们使用重剖优化带修的部分，可以在 \(\Theta(\log^2n)\) 的复杂度下实现单点修改。

将这棵树剖分后，假如有这样一条重链：

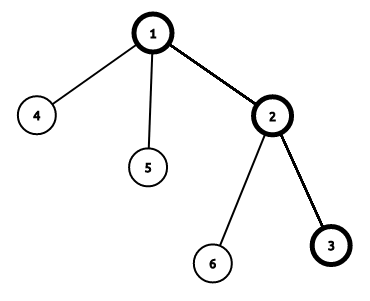
设 \(g_{i,0}\) 表示不选择 \(i\) 且只允许选择 \(i\) 的轻儿子所在子树的最大答案，

\(g_{i,1}\) 表示不考虑 \(son_i\) 的情况下选择 \(i\) 的最大答案，

\(son_i\) 表示 \(i\) 的重儿子。

则刚才的方程就简化为：

\[\begin{cases} dp_{i,0}=g_{i,0}+\max(dp_{son_i,0},dp_{son_i,1})\\ dp_{i,1}=g_{i,1}+dp_{son_i,0} \end{cases} \]

最后答案 \(ans=\max(dp_{rt,0},dp_{rt,1})\)。

然后我们现在要考虑如何在线段树内 \(\Theta(1)\) 的修改与查询。

矩阵乘法

我们发现这可以用矩阵乘法优化。

但与一般的矩乘不同，我们要用的是广义矩阵乘法。

定义广义矩阵乘法 \(A\times B=C\) 为：

\[C_{i,j}=\max\limits_{k=1}^n(A_{i,k}+B_{k,j}) \]

相当于将普通的矩阵乘法中的乘变为加，加变为 \(\max\) 操作。

同时广义矩阵乘法满足结合律，所以可以使用矩阵快速幂。

可以构造出矩阵：

\[\begin{bmatrix} dp_{son_i,0}\\ dp_{son_i,1} \end{bmatrix} \times \begin{bmatrix} g_{i,0} & g_{i,0}\\ g_{i,1} & -\infty \end{bmatrix} = \begin{bmatrix} dp_{i,0}\\ dp_{i,1} \end{bmatrix} \]

例题

P4719【模板】"动态 DP"&动态树分治

思路如上。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN=1e5+5;
const int INF=0x7f7f7f7f;

int n,m;
int dp[MAXN][2],g[MAXN][2];

struct edge
{
    int to,nxt;
}e[MAXN<<1];

int head[MAXN],cnt;

inline void add(int x,int y)
{
    e[++cnt].to=y;
    e[cnt].nxt=head[x];
    head[x]=cnt;
    return;
}

int siz[MAXN],hson[MAXN],fa[MAXN],dep[MAXN];

struct Matrix
{
    int m[2][2];
    inline void clear()
    {
        for(int i=0;i<=1;i++)
            for(int j=0;j<=1;j++) m[i][j]=-INF;
        return;
    }
    inline Matrix operator*(const Matrix &b)const
    {
        Matrix ans; ans.clear();
        for(int i=0;i<=1;i++)
            for(int j=0;j<=1;j++)
                for(int k=0;k<=1;k++)
                    ans.m[i][j]=max(ans.m[i][j],m[i][k]+b.m[k][j]);
        return ans;
    }
}t[MAXN<<2],a[MAXN],ans;

inline void dfs1(int x,int f)
{
    dep[x]=dep[f]+1;
    siz[x]=1; fa[x]=f;
    int maxson=-1;
    for(int i=head[x];i;i=e[i].nxt)
    {
        int y=e[i].to;
        if(y==f) continue;
        dfs1(y,x);
        siz[x]+=siz[y];
        if(maxson<siz[y])
        {
            maxson=siz[y];
            hson[x]=y;
        }
    }
    return;
}

int now,id[MAXN],nval[MAXN],val[MAXN],top[MAXN],ed[MAXN];

inline void dfs2(int x,int ltop)
{
    id[x]=++now;
    nval[now]=x;
    top[x]=ltop;
    ed[ltop]=now;
    if(!hson[x]) return;
    dfs2(hson[x],ltop);
    for(int i=head[x];i;i=e[i].nxt)
    {
        int y=e[i].to;
        if(y==fa[x] || y==hson[x]) continue;
        dfs2(y,y);
    }
    return;
}

inline void dfs3(int x)
{
    dp[x][1]=val[x];
    for(int i=head[x];i;i=e[i].nxt)
    {
        int y=e[i].to;
        if(y==fa[x] || y==hson[x]) continue;
        dfs3(y);
        dp[x][0]+=max(g[y][1],g[y][0]);
        dp[x][1]+=g[y][0];
    }
    g[x][0]+=dp[x][0];
    g[x][1]+=dp[x][1];
    if(!hson[x]) return;
    dfs3(hson[x]);
    g[x][0]+=max(g[hson[x]][1],g[hson[x]][0]);
    g[x][1]+=g[hson[x]][0];
    return;
}

inline void pushup(int p)
{
    t[p]=t[p<<1]*t[p<<1|1];
    return;
}

inline void build(int p,int l,int r)
{
    if(l==r)
    {
        a[nval[l]].m[0][0]=dp[nval[l]][0],a[nval[l]].m[1][0]=dp[nval[l]][1];
        a[nval[l]].m[0][1]=dp[nval[l]][0],a[nval[l]].m[1][1]=-INF;
        t[p]=a[nval[l]]; return;
    }
    int mid=(l+r)>>1;
    build(p<<1,l,mid),build(p<<1|1,mid+1,r);
    pushup(p); return;
}

inline void change(int p,int l,int r,int x)
{
    if(l==r) {t[p]=a[nval[x]];return;}
    int mid=(l+r)>>1;
    if(x<=mid) change(p<<1,l,mid,x);
    else change(p<<1|1,mid+1,r,x);
    pushup(p); return;
}

inline Matrix ask(int p,int l,int r,int a,int b)
{
    if(l>=a && r<=b) return t[p];
    int mid=(l+r)>>1;
    if(b<=mid) return ask(p<<1,l,mid,a,b);
    if(a>mid) return ask(p<<1|1,mid+1,r,a,b);
    return ask(p<<1,l,mid,a,b)*ask(p<<1|1,mid+1,r,a,b);
}

inline void solve(int x,int k)
{
    a[x].m[1][0]+=k-val[x],val[x]=k;
    while(x)
    {
        Matrix nx,ny;
        int nowx=top[x];
        nx=ask(1,1,n,id[nowx],ed[nowx]);
        change(1,1,n,id[x]);
        ny=ask(1,1,n,id[nowx],ed[nowx]);
        x=fa[nowx];
        a[x].m[0][0]+=max(ny.m[0][0],ny.m[1][0])-max(nx.m[0][0],nx.m[1][0]);
        a[x].m[0][1]=a[x].m[0][0];
        a[x].m[1][0]+=ny.m[0][0]-nx.m[0][0];
    }
    return;
}

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>val[i];
    for(int i=1;i<=n-1;i++)
    {
        int x,y; cin>>x>>y;
        add(x,y),add(y,x);
    }
    dfs1(1,0),dfs2(1,1),dfs3(1),build(1,1,n);
    for(int i=1;i<=m;i++)
    {
        int x,y; cin>>x>>y;
        solve(x,y);
        ans=ask(1,1,n,id[1],ed[1]);
        printf("%lld\n",max(ans.m[0][0],ans.m[1][0]));
    }
    return 0;
}

P5024 [NOIP2018 提高组] 保卫王国

跟上面那个没差多少。

因为最小权覆盖集 = 全集 - 最大权独立集。

所以直接修改查询就可以了。

当城市 \(a\) 不得驻扎军队时。

将 \(a\) 增加 \(\infty\)。

当城市 \(a\) 必须驻扎军队时。

将 \(a\) 减少 \(\infty\)。

如果查询的答案为 \(\infty\)。

则为无解。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN=1e5+5;
const int INF=1e10;

int n,m;
int dp[MAXN][2],g[MAXN][2];

struct edge
{
    int to,nxt;
}e[MAXN<<1];

int head[MAXN],cnt;

inline void add(int x,int y)
{
    e[++cnt].to=y;
    e[cnt].nxt=head[x];
    head[x]=cnt;
    return;
}

int siz[MAXN],hson[MAXN],fa[MAXN],dep[MAXN];

struct Matrix
{
    int m[2][2];
    inline void clear()
    {
        for(int i=0;i<=1;i++)
            for(int j=0;j<=1;j++) m[i][j]=-INF;
        return;
    }
    inline Matrix operator*(const Matrix &b)const
    {
        Matrix ans; ans.clear();
        for(int i=0;i<=1;i++)
            for(int j=0;j<=1;j++)
                for(int k=0;k<=1;k++)
                    ans.m[i][j]=max(ans.m[i][j],m[i][k]+b.m[k][j]);
        return ans;
    }
}t[MAXN<<2],a[MAXN],ans;

inline void dfs1(int x,int f)
{
    dep[x]=dep[f]+1;
    siz[x]=1; fa[x]=f;
    int maxson=-1;
    for(int i=head[x];i;i=e[i].nxt)
    {
        int y=e[i].to;
        if(y==f) continue;
        dfs1(y,x);
        siz[x]+=siz[y];
        if(maxson<siz[y])
        {
            maxson=siz[y];
            hson[x]=y;
        }
    }
    return;
}

int now,id[MAXN],nval[MAXN],val[MAXN],top[MAXN],ed[MAXN];

inline void dfs2(int x,int ltop)
{
    id[x]=++now;
    nval[now]=x;
    top[x]=ltop;
    ed[ltop]=now;
    if(!hson[x]) return;
    dfs2(hson[x],ltop);
    for(int i=head[x];i;i=e[i].nxt)
    {
        int y=e[i].to;
        if(y==fa[x] || y==hson[x]) continue;
        dfs2(y,y);
    }
    return;
}

inline void dfs3(int x)
{
    dp[x][1]=val[x];
    for(int i=head[x];i;i=e[i].nxt)
    {
        int y=e[i].to;
        if(y==fa[x] || y==hson[x]) continue;
        dfs3(y);
        dp[x][0]+=max(g[y][1],g[y][0]);
        dp[x][1]+=g[y][0];
    }
    g[x][0]+=dp[x][0];
    g[x][1]+=dp[x][1];
    if(!hson[x]) return;
    dfs3(hson[x]);
    g[x][0]+=max(g[hson[x]][1],g[hson[x]][0]);
    g[x][1]+=g[hson[x]][0];
    return;
}

inline void pushup(int p)
{
    t[p]=t[p<<1]*t[p<<1|1];
    return;
}

inline void build(int p,int l,int r)
{
    if(l==r)
    {
        a[nval[l]].m[0][0]=dp[nval[l]][0],a[nval[l]].m[1][0]=dp[nval[l]][1];
        a[nval[l]].m[0][1]=dp[nval[l]][0],a[nval[l]].m[1][1]=-INF;
        t[p]=a[nval[l]]; return;
    }
    int mid=(l+r)>>1;
    build(p<<1,l,mid),build(p<<1|1,mid+1,r);
    pushup(p); return;
}

inline void change(int p,int l,int r,int x)
{
    if(l==r) {t[p]=a[nval[x]];return;}
    int mid=(l+r)>>1;
    if(x<=mid) change(p<<1,l,mid,x);
    else change(p<<1|1,mid+1,r,x);
    pushup(p); return;
}

inline Matrix ask(int p,int l,int r,int a,int b)
{
    if(l>=a && r<=b) return t[p];
    int mid=(l+r)>>1;
    if(b<=mid) return ask(p<<1,l,mid,a,b);
    if(a>mid) return ask(p<<1|1,mid+1,r,a,b);
    return ask(p<<1,l,mid,a,b)*ask(p<<1|1,mid+1,r,a,b);
}

inline void solve(int x,int k)
{
    a[x].m[1][0]+=k,val[x]+=k;
    while(x)
    {
        Matrix nx,ny;
        int nowx=top[x];
        nx=ask(1,1,n,id[nowx],ed[nowx]);
        change(1,1,n,id[x]);
        ny=ask(1,1,n,id[nowx],ed[nowx]);
        x=fa[nowx];
        a[x].m[0][0]+=max(ny.m[0][0],ny.m[1][0])-max(nx.m[0][0],nx.m[1][0]);
        a[x].m[0][1]=a[x].m[0][0];
        a[x].m[1][0]+=ny.m[0][0]-nx.m[0][0];
    }
    return;
}

string type;

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin>>n>>m>>type;
    int sum=0;
    for(int i=1;i<=n;i++) cin>>val[i],sum+=val[i];
    for(int i=1;i<=n-1;i++)
    {
        int x,y; cin>>x>>y;
        add(x,y),add(y,x);
    }
    dfs1(1,0),dfs2(1,1),dfs3(1),build(1,1,n);
    for(int i=1;i<=m;i++)
    {
        int x1,y1,x2,y2,res=0; cin>>x1>>y1>>x2>>y2;
        if(y1) solve(x1,-INF); else solve(x1,INF);
        if(y2) solve(x2,-INF); else solve(x2,INF);
        res=((y1^1)+(y2^1))*INF;
        ans=ask(1,1,n,id[1],ed[1]);
        res=max(ans.m[0][0],ans.m[1][0])-res;
        if(y1) solve(x1,INF); else solve(x1,-INF);
        if(y2) solve(x2,INF); else solve(x2,-INF);
        if(sum-res>INF) printf("-1\n");
        else printf("%lld\n",sum-res);
    }
    return 0;
}