【数据结构】红黑树 详解
在我们学习 JDK1.8 的 HashMap 和 ConcurrentHashMap 前，
先来了解一种 数据结构 —— 红黑树:
首先，没有基础的同学可能问如下问题：
什么是 红黑树？
红黑树（Red Black Tree）是一种 自平衡二叉查找树，
是在计算机科学中用到的一种数据结构，典型的用途是 实现关联数组
红黑树是在1972年由Rudolf Bayer发明的，当时被称为 平衡二叉B树（symmetric binary B-trees）
后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”
红黑树是一种 特化 的 AVL树（平衡二叉树），都是在进行 插入 和 删除 操作时，
通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能
它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，
并且在实践中是高效的： 它可以在 O(log n)时间内 做 查找、插入 和 删除，这里的n 是树中元素的数目
(摘自 百度百科)
可能会有同学像本人一样，看完后不知道学到了什么，
那么，本人在这里简要总结下：
红黑树就是 优化了查询效率 的 AVL树
那么，相信许多同学一定了解，要学习红黑树，就要牢记它的 五大特性:
五大特性：
1、节点颜色 非红即黑
2、根 必 黑
3、叶子(NIL) 必 黑
(在 Java 中，叶子结点 是为 null 的结点)
4、红色节点 的 两个子节点 必 黑
5、任意一结点 到 每个叶子结点 的 任一路径 都包含 数量相同 的 黑结点（完美黑色平衡）
在研究 红黑树 的过程中，我们要牢记如下几个重要节点：
重要节点：
种类：
当前节点
兄弟节点
父节点
叔叔节点
祖父节点
关系图：
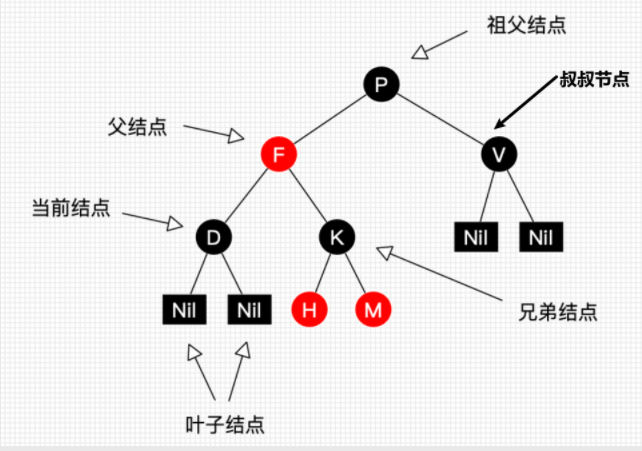
在 红黑树 的 节点插入、删除 过程中，最重要的步骤有三点：
重要步骤：
种类：
左旋
右旋
变色
左旋：
以某个结点作为支点(旋转结点)，
其右子结点变为旋转结点的父结点，
右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变
如下图所示：
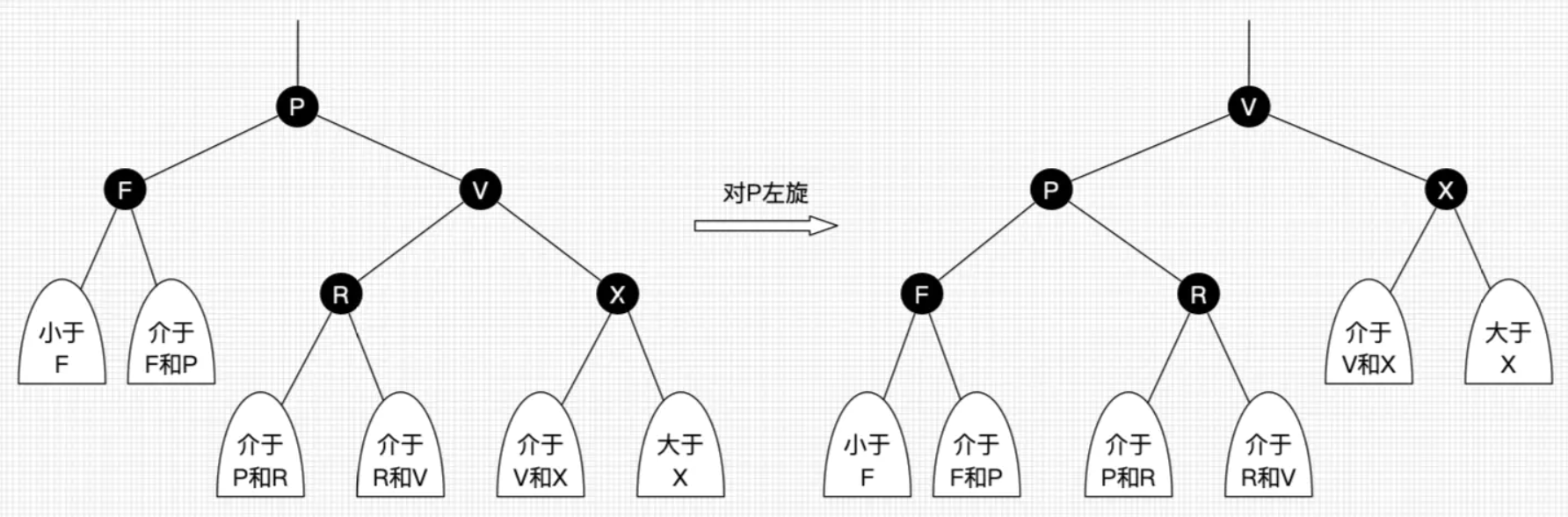
右旋：
以某个结点作为支点(旋转结点)，
其左子结点变为旋转结点的父结点，
左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变
如下图所示：
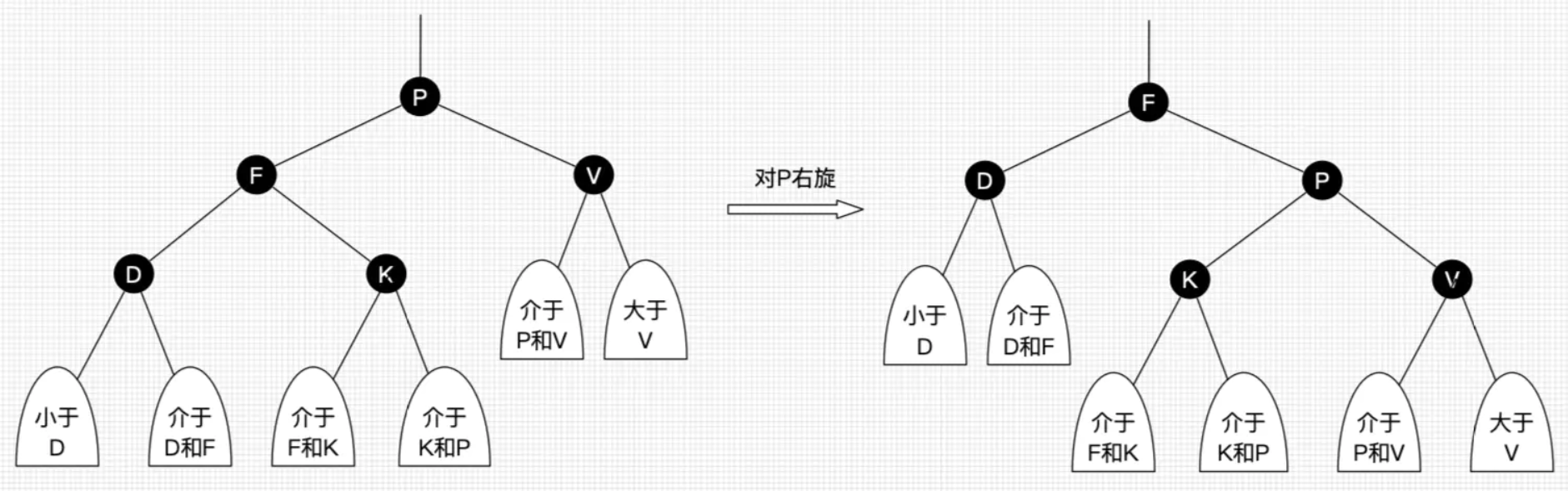
变色：
顾名思义：
红色 -> 黑色
黑色 -> 红色
对于 红黑树，主要的操作 就是 查找、插入、删除
(至于 链表树化，无非是 先转换根节点，然后插入其它节点
至于 红黑树反树化，几乎跟红黑树性质不搭边)
那么，本人就先来讲解下 三大操作 中最简单的 节点查找操作：
节点查找：
步骤：
- 从根结点开始查找，把根结点设置为当前结点；
- 若当前结点为空，返回null；
- 若当前结点不为空，用当前结点的key跟查找key作比较；
- 若当前结点key等于查找key，那么该key就是查找目标，返回当前结点；
- 若当前结点key大于查找key，把当前结点的左子结点设置为当前结点，重复步骤2；(AVL树性质)
- 若当前结点key小于查找key，把当前结点的右子结点设置为当前结点，重复步骤2；(AVL树性质)
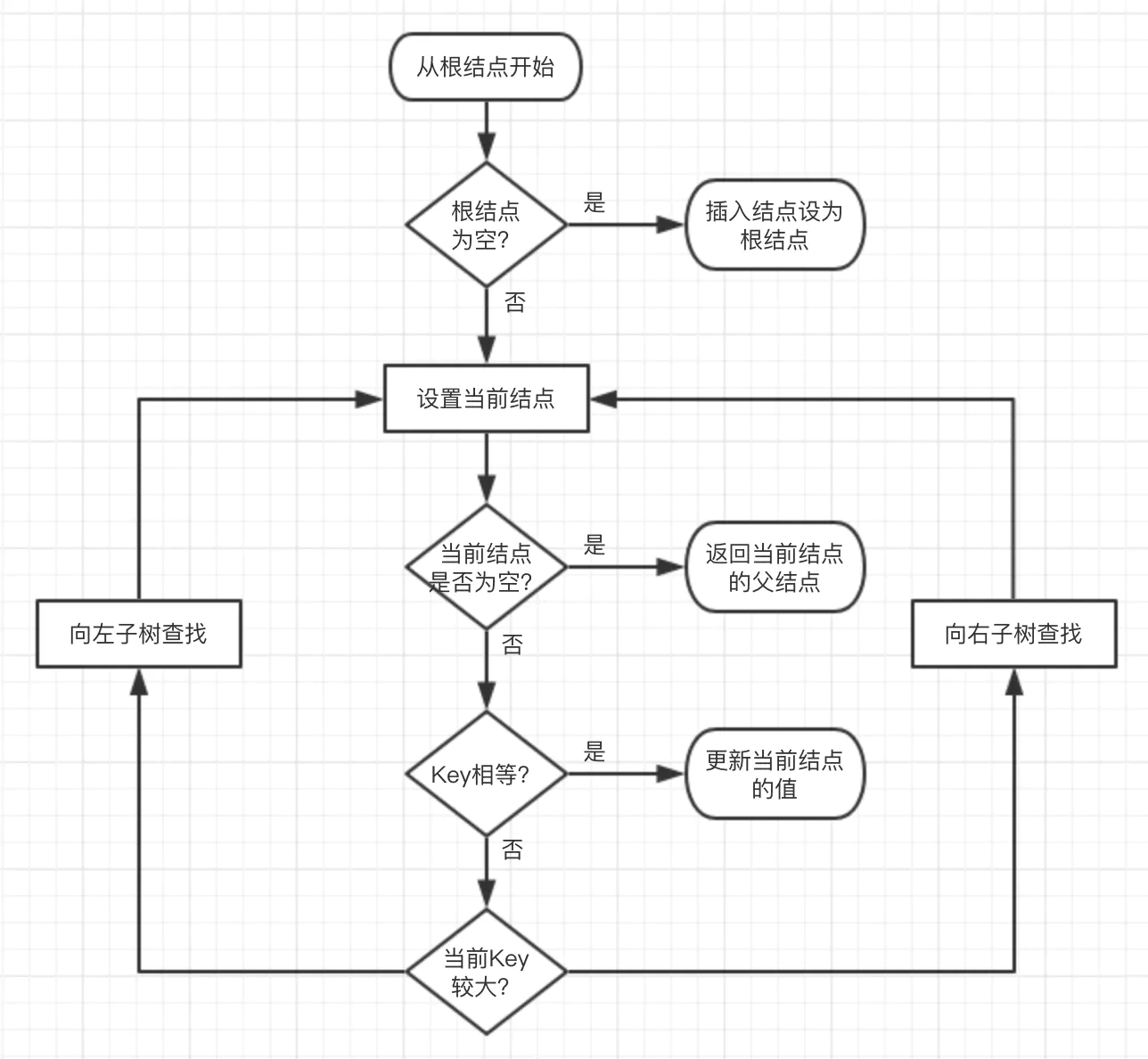
那么，本人根据上述步骤，来给出一个 流程图:
流程图：
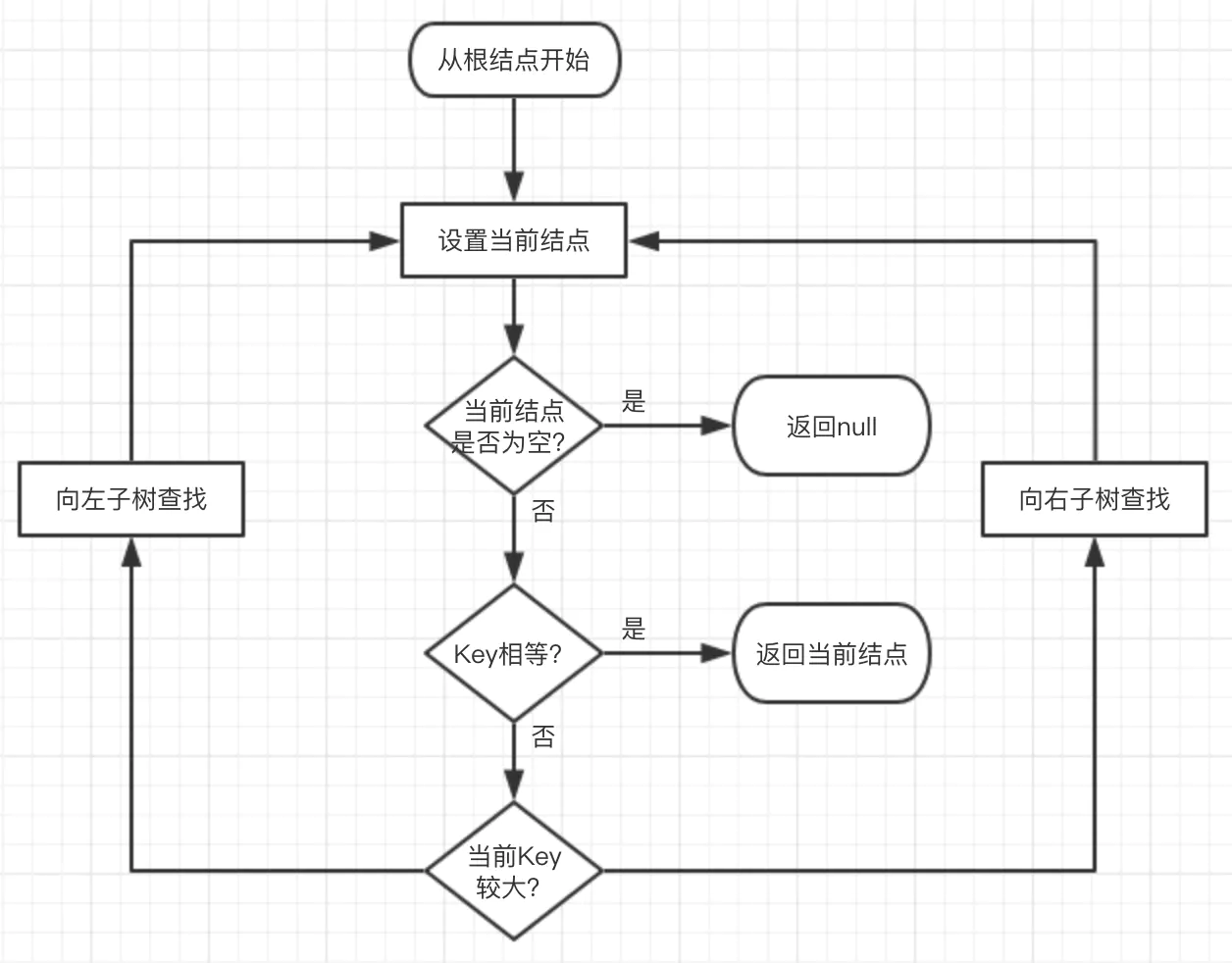
相信 看完上述的讲解和流程图，同学们对于 红黑树的节点查找操作流程 很明白了！
那么，接下来，本人来讲解下 红黑树的 节点插入操作：
节点插入：
红黑树 的 节点插入操作，大致来讲分为如下三步：
大致概括：
- 查找 插入位置
- 插入 目标节点
- 平衡化 当前树
同样地，本人根据上述步骤，来给出一个 流程图:
流程图：
查找插入位置：
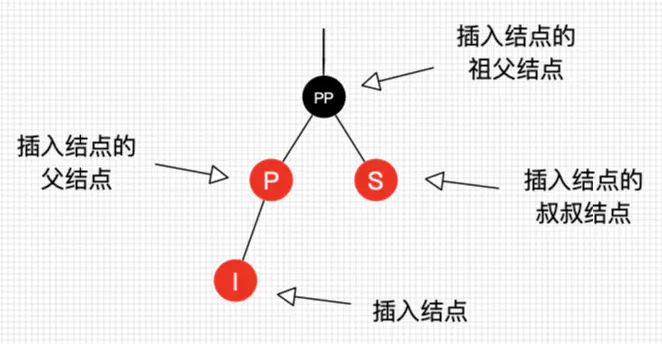
在讲解 插入后平衡操作 之前，为了方便同学们的学习，本人先来给出 各节点关系图：
插入节点后，平衡化：
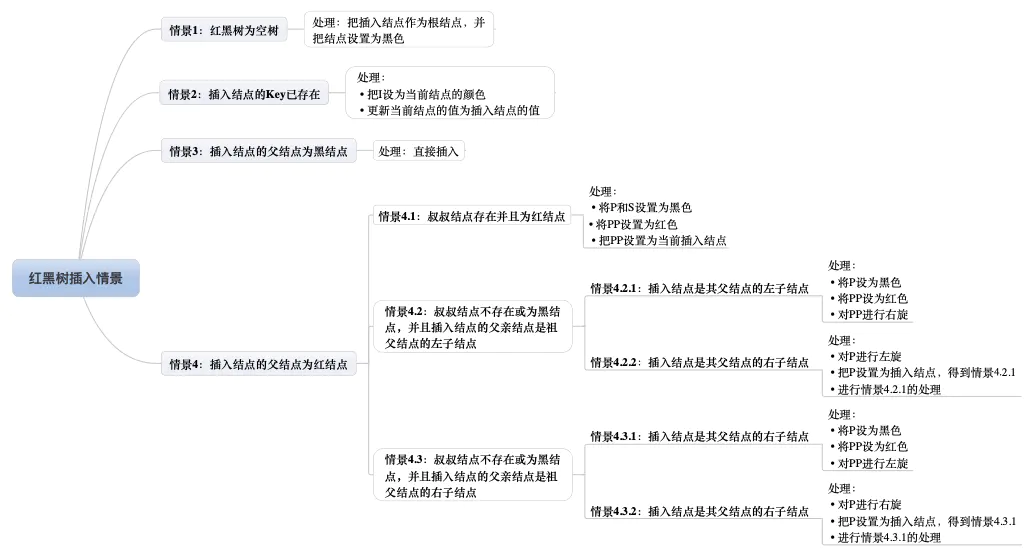
这里的 节点插入后平衡操作，是 红黑树的精髓 之一
节点删除：
红黑树 的 节点插入操作，大致来讲分为如下三步：
大致概括：
- 查找 目标节点
- 删除 目标节点
- 平衡化 当前树
同样地，本人根据上述步骤，来给出一个 流程图:
流程图：
至于查找目标节点的操作，和 节点查找操作 的步骤一致，本人就不展示了
在讲解 删除后平衡操作 之前，为了方便同学们的学习，本人先来给出 各节点关系图：
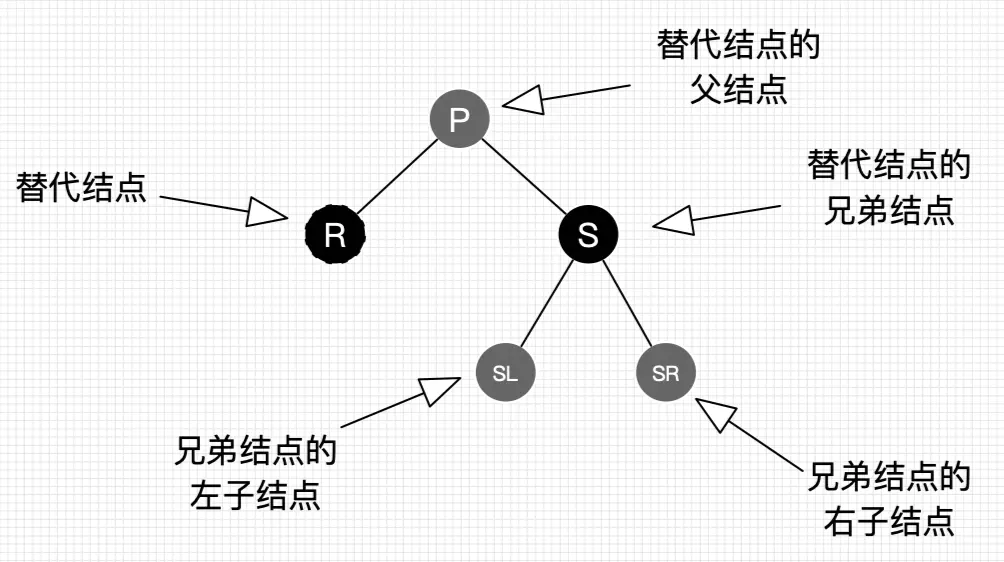
删除节点后，平衡化：
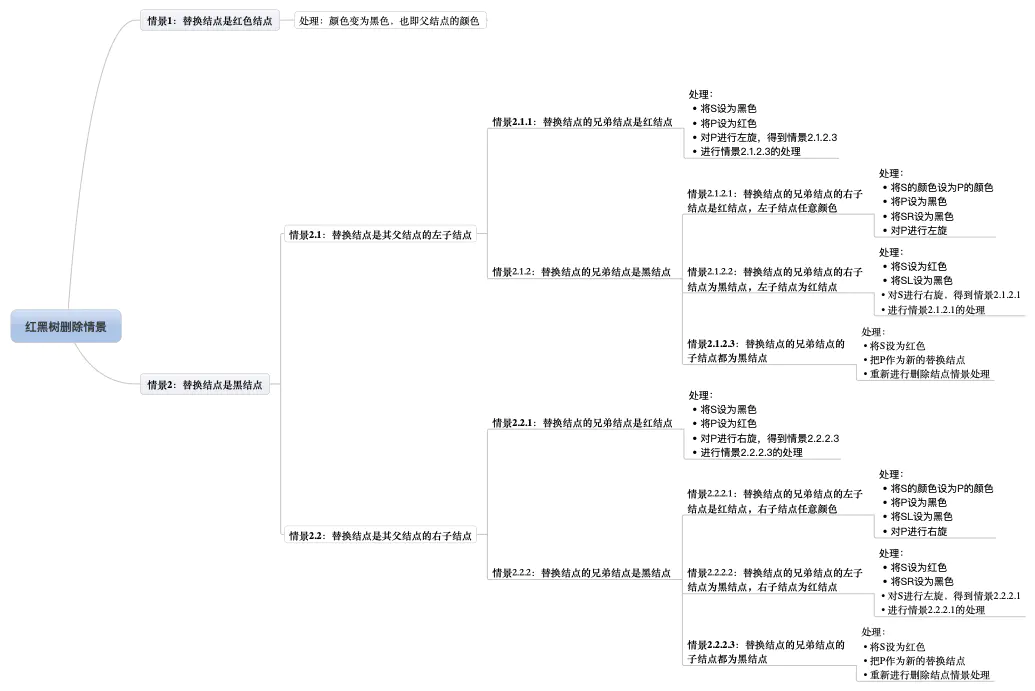
那么，到这里，红黑树的基本知识点就讲解完毕了！
因为本文的主要目的是 介绍红黑树的基本知识点，以便后续博文中对HashMap 和 ConcurrentHashMap 的 源码分析
所以本文的有些讲解有些仓促，但是知识点都是正确且详细的，只是案例展示没有提供
那么，在之后的博文中，本人将依据本篇博文所讲解的知识点，来与同学们一起 剖析 HashMap 和 ConcurrentHashMap 的 红黑树相关源码，敬请关注！😉
最后附上 超详细的 参考博文：
