【算法精研】动态规划总集篇

shadow-logo

每当谈及 动态规划，就会被问到如下问题：

什么是 `动态规划`？

概念：

动态规划（Dynamic Programming，简称“DP”）
是运筹学的一个分支，是求解决策过程最优化的过程。
20世纪50年代初，美国数学家贝尔曼（R.Bellman）等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理，从而创立了动态规划。
动态规划的应用极其广泛，包括工程技术、经济、工业生产、军事以及自动化控制等领域，并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果

(摘自百度百科)

动态规划的原理是什么？

原理：

在现实生活中，有一类活动的过程，
由于它的特殊性，可将过程分成若干个互相联系的阶段，
在它的每一阶段都需要作出决策，从而使 整个过程 达到最好的活动效果
因此各个阶段决策的选取不能任意确定，
它 依赖于当前面临的状态，又 影响以后的发展
当各个阶段决策确定后，就组成一个 决策序列，因而也就确定了整个过程的一条活动路线．
这种把一个问题看作是一个 前后关联、具有链状结构的多阶段过程就称为 多阶段决策过程，这种问题称为 多阶段决策问题
在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，
一个决策序列就是在 变化的状态 中产生出来的，故有“动态”的含义，
称这种解决 多阶段决策最优化 的过程为 动态规划 方法

(摘自百度百科)

那么，根据上述的讲解，本人来用一句话概括：

动态规划 就是计算 多阶段问题的全局最优解 的 递推算法

动态规划和贪心的区别是什么？

区别：

	动态规划	贪心算法
顺序	自底向上	自顶向下
性质	全局最优解	局部最优解

相信很多同学都见过如上两条区别，但是能彻底理解的确是不多

那么，本人现在来讲解下上述两点区别：

顺序角度：

贪心算法：

贪心算法中，作出的 每步贪心决策 都 无法改变，
因为贪心策略是由上一步的最优解 推导 下一步的最优解，
而 上一步之前的最优解 则 不作保留

动态规划：

全局最优解中一定包含 某个局部最优解，但不一定包含前一个局部最优解，因此需要记录之前的所有最优解

性质角度：

贪心算法：

贪心算法中，是根据之前的条件，来推导 当前最优结果

动态规划：

动态规划则是根据之后的情况，来推导 当前最优结果

动态规划有哪些题型呢？

斐波那契数列
矩阵路径
数组区间
分割整数
最长递增序列
最长公共子序列
0-1背包
股票交易
字符串编辑

那么，介绍了这么多冷冰冰的概念，
接下来，本人就来通过些许例题，来带同学们了解并巩固下 动态规划 吧！

斐波那契数列系列：

斐波那契数列问题：

题目描述：

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例：

示例1：

输入：n = 2
输出：1

示例2：

n = 5
5

提示：

0 <= n <= 100

题解：

题解链接

母牛繁殖问题：

题目描述：

假设农场中成熟的母牛每年都会生 1 头小母牛，并且永远不会死。
第一年有 1 只小母牛，从第二年开始，母牛开始生小母牛。
每只小母牛 3 年之后成熟又可以生小母牛。
给定整数 n，求 n 年后牛的数量。

题解：

public class Solution {

    public int rob(int n) {
        if (n <= 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        if (n == 2) {
            return 2;
        }
        if (n == 3) {
            return 4;
        }

        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 4;
        for (int i = 2; i < n; i++) {
            dp[i] = dp[i - 1] + dp[i - 3];
        }
        return dp[n];
    }

}

爬楼梯问题：

题目描述：

假设你正在爬楼梯。
需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。
你有多少种不同的方法可以爬到楼顶呢？

注意：

给定 n 是一个正整数。

示例：

示例 1：

输入： 2
输出： 2
解释：有两种方法可以爬到楼顶。

1 阶 + 1 阶

2 阶

示例 2：

输入： 3
输出： 3
解释：有三种方法可以爬到楼顶。

1 阶 + 1 阶 + 1 阶

1 阶 + 2 阶

2 阶 + 1 阶

题解：

题解链接

强盗抢劫Ⅰ—— 串形房屋：

题目描述：

你是一个专业的小偷，计划偷窃沿街的房屋。
每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，
给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额

示例：

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。

提示：

1、0 <= nums.length <= 100
2、0 <= nums[i] <= 400

题解：

题解链接

强盗抢劫Ⅱ—— 环形房屋：

题目描述：

你是一个专业的小偷，计划偷窃沿街的房屋。
这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。
同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额

示例：

示例 1：

输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

示例 3：

输入：nums = [0]
输出：0

提示：

1、1 <= nums.length <= 100
2、0 <= nums[i] <= 1000

题解：

题解链接

矩阵路径系列：

最小路径和问题：

题目描述：

给定一个包含非负整数的 m x n 网格 grid ，
请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：

每次只能向下或者向右移动一步。

注意：

给定 n 是一个正整数。

示例：

示例 1：

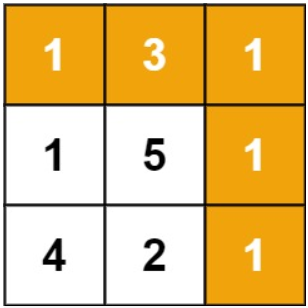
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

1、m == grid.length
2、n == grid[i].length
3、1 <= m, n <= 200
4、0 <= grid[i][j] <= 100

题解：

题解链接

不同路径：

题目描述：

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
问总共有多少条不同的路径？

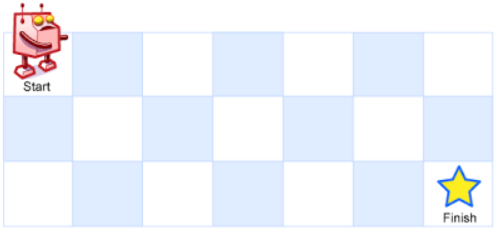
示例：

示例 1：

输入：m = 3, n = 2
输出：3
解释：从左上角开始，总共有 3 条路径可以到达右下角：

向右 -> 向右 -> 向下

向右 -> 向下 -> 向右

向下 -> 向右 -> 向右

示例 2：

输入：m = 7, n = 3
输出：28

提示：

1、1 <= m, n <= 100
2、题目数据保证答案小于等于 2 * 10 ^ 9

题解：

题解链接

数组区间问题：

区域和检索 - 数组不可变：

题目描述：

给定一个整数数组 nums，求出数组从索引 i 到 j（i ≤ j）范围内元素的总和，包含 i、j 两点。
实现 NumArray 类：

1.NumArray(int[] nums) 使用数组 nums 初始化对象
2. int sumRange(int i, int j) 返回数组 nums 从索引 i 到 j（i ≤ j）范围内元素的总和，
包含 i、j 两点（也就是 sum(nums[i], nums[i + 1], ... , nums[j])）

示例：

示例 1：

输入：

["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]

输出：

[null, 1, -1, -3]

解释：

NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

提示：

1、0 <= nums.length <= 104
2、-105 <= nums[i] <= 105
3、0 <= i <= j < nums.length
4、最多调用 104 次 sumRange 方法

题解：

题解链接

等差递增子区间:

题目描述：

如果一个数列至少有三个元素，并且任意两个相邻元素之差相同，则称该数列为等差数列。
例如，以下数列为等差数列:

1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9

以下数列不是等差数列。

1, 1, 2, 5, 7

数组 A 包含 N 个数，且索引从0开始。数组 A 的一个子数组划分为数组 (P, Q)，P 与 Q 是整数且满足 0<=P<Q<N 。
如果满足以下条件，则称子数组(P, Q)为等差数组：

元素 A[P], A[p + 1], ..., A[Q - 1], A[Q] 是等差的。并且 P + 1 < Q 。

函数要返回数组 A 中所有为等差数组的子数组个数。

示例：

示例 1：

A = [1, 2, 3, 4]
返回: 3, A 中有三个子等差数组: [1, 2, 3], [2, 3, 4] 以及自身 [1, 2, 3, 4]。

题解：

题解链接

分割数组系列：

解码方法:

题目描述：

一条包含字母 A-Z 的消息通过以下方式进行了编码：
'A' -> 1
'B' -> 2
...
'Z' -> 26
给定一个只包含数字的非空字符串，请计算解码方法的总数。
题目数据保证答案肯定是一个 32 位的整数。

示例：

示例 1：

输入：s = "12"
输出：2
解释：它可以解码为 "AB"（1 2）或者 "L"（12）。

示例 2：

输入：s = "226"
输出：3
解释：它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。

示例 3：

输入：s = "0"
输出：0

示例 4：

输入：s = "1"
输出：1

示例 5：

输入：s = "2"
输出：1

提示：

1 <= s.length <= 100

s 只包含数字，并且可能包含前导零。

题解：

题解链接

完全平方数:

题目描述：

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。
你需要让组成和的完全平方数的个数最少。

示例：

示例 1：

输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.

示例 2：

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

题解：

题解链接

整数拆分:

题目描述：

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。
返回你可以获得的最大乘积。

示例：

示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2：

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

说明:

你可以假设 n 不小于 2 且不大于 58。

题解：

题解链接

最长子序列系列：

最长上升子序列：

题目描述：

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例：

输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

说明:

可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。

进阶：

你能将算法的时间复杂度降低到 O(n log n) 吗?

题解：

题解链接

最长数对链：

题目描述：

给出 n 个数对。在每一个数对中，第一个数字总是比第二个数字小。
现在，我们定义一种跟随关系，当且仅当 b < c 时，数对(c, d) 才可以跟在 (a, b) 后面。
我们用这种形式来构造一个数对链。
给定一个数对集合，找出能够形成的最长数对链的长度。
你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。

示例：

输入：[[1,2], [2,3], [3,4]]
输出：2
解释：最长的数对链是 [1,2] -> [3,4]

说明:

给出数对的个数在 [1, 1000] 范围内。

题解：

题解链接

最长摆动子序列：

题目描述：

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。
第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。
例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。
相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
给定一个整数序列，返回作为摆动序列的最长子序列的长度。
通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

示例：

示例 1：

输入: [1,7,4,9,2,5]
输出: 6
解释: 整个序列均为摆动序列。

示例 2：

输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列，其中一个可为[1,17,10,13,10,16,8]。

示例 3:

输入: [1,2,3,4,5,6,7,8,9]
输出: 2

进阶:

你能否用 O(n) 时间复杂度完成此题?

题解：

题解链接

最长公共子序列系列:

最长公共子序列:

题目描述：

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。
一个字符串的子序列是指这样一个新的字符串：

它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如:

"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。
两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例：

示例 1：

输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace"，它的长度为 3。

示例 2：

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc"，它的长度为 3。

示例 3：

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0。

提示:

1 <= text1.length <= 1000

1 <= text2.length <= 1000

输入的字符串只含有小写英文字符。

题解：

题解链接

0/1背包系列:

划分数组为和相等的两部分:

题目描述：

给定一个只包含正整数的非空数组。
是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意：

每个数组中的元素不会超过 100
数组的大小不会超过 200

示例：

示例 1：

输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2：

输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.

题解：

题解链接

目标和:

题目描述：

给定一个非负整数数组，a1, a2, ..., an, 和一个目标数，S。
现在你有两个符号+和-。
对于数组中的任意一个整数，你都可以从+或-中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例：

输入：nums: [1, 1, 1, 1, 1], S: 3
输出：5
解释：
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。

提示:

1、数组非空，且长度不会超过 20 。
2、初始的数组的和不会超过 1000 。
3、保证返回的最终结果能被 32 位整数存下。

题解：

题解链接

一和零:

题目描述：

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小，该子集中最多有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的子集。

示例：

示例 1：

输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。
{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {"0", "1"} ，所以答案是 2 。

提示:

1、1 <= strs.length <= 600
2、1 <= strs[i].length <= 100
3、strs[i]仅由'0' 和'1' 组成
4、1 <= m, n <= 100

题解：

题解链接

股票交易系列：

最佳买卖股票时机含冷冻期:

题目描述：

给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格。
设计一个算法计算出最大利润。
在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

示例：

输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

题解：

题解链接

字符串编辑系列：

两个字符串的删除操作:

题目描述：

给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，
每步可以删除任意一个字符串中的一个字符。

示例：

输入: "sea", "eat"
输出: 2
解释: 第一步将"sea"变为"ea"，第二步将"eat"变为"ea"

提示:

1、给定单词的长度不超过500。
2、给定单词中的字符只含有小写字母。

题解：

题解链接

posted @ 2020-12-01 14:01 在下右转，有何贵干阅读(1388) 评论(0) 编辑收藏举报

刷新页面返回顶部

在下右转，有何贵干

带你深究Java的本质！

【算法精研】动态规划 总集篇

什么是 动态规划？

动态规划 的原理是什么？

动态规划 和 贪心 的区别是什么？

顺序角度：

贪心算法：

动态规划：

性质角度：

贪心算法：

动态规划：

动态规划 有哪些题型呢？

斐波那契数列 系列：

斐波那契数列 问题：

题目描述：

示例：

提示：

题解：

母牛繁殖 问题：

题目描述：

题解：

爬楼梯 问题：

题目描述：

注意：

示例：

题解：

强盗抢劫Ⅰ—— 串形房屋：

题目描述：

示例：

提示：

题解：

强盗抢劫Ⅱ—— 环形房屋：

题目描述：

示例：

提示：

题解：

矩阵路径 系列：

最小路径和 问题：

题目描述：

说明：

注意：

示例：

提示：

题解：

不同路径：

题目描述：

示例：

提示：

题解：

数组区间 问题：

区域和检索 - 数组不可变：

题目描述：

示例：

提示：

题解：

等差递增子区间:

题目描述：

示例：

题解：

分割数组 系列：

解码方法:

题目描述：

示例：

提示：

题解：

完全平方数:

题目描述：

示例：

题解：

整数拆分:

题目描述：

示例：

说明:

题解：

最长子序列 系列：

最长上升子序列：

题目描述：

示例：

说明:

【算法精研】动态规划总集篇

什么是 `动态规划`？

动态规划的原理是什么？

动态规划和贪心的区别是什么？

动态规划有哪些题型呢？

斐波那契数列系列：

斐波那契数列问题：

母牛繁殖问题：

爬楼梯问题：

矩阵路径系列：

最小路径和问题：

数组区间问题：

分割数组系列：

最长子序列系列：

最长公共子序列系列:

0/1背包系列:

股票交易系列：

字符串编辑系列：