Java数组 —— 八大排序
(请观看本人博文——《详解 普通数组 —— Arrays类 与 浅克隆》)
在本人《数据结构与算法》专栏的讲解中,本人讲解了如何去实现数组的八大排序。
但是,在讲解的过程中,我们能够发现:这些几乎都和指针相关
同学们可能就会和本人一样,想到了Java中不存在指针的概念,
那么,该如何去实现呢?
本人在这里要提出的一点是:
虽然Java不存在指针,但是,Java处处都是指针。
这句话可能在本人的《Java SE》专栏的前期博文中大家经常能够看到。
那么,现在,本人就来讲解下在Java中,这八大排序该如何实现:
冒泡排序
时间复杂度:
O(n^2)
基本原理:
每一个数与它后面的数相比较,最终每一轮排完都会将未排序中最大(或最小)的数排在适当的位置
动态演示:
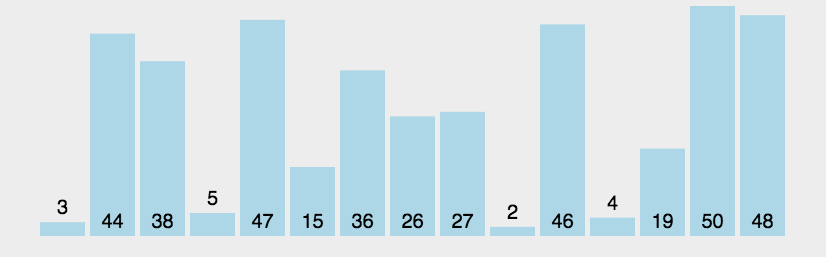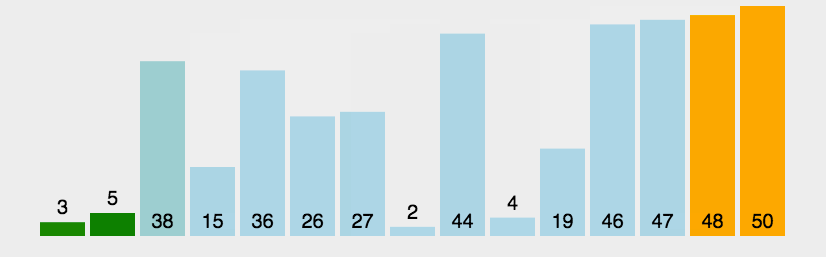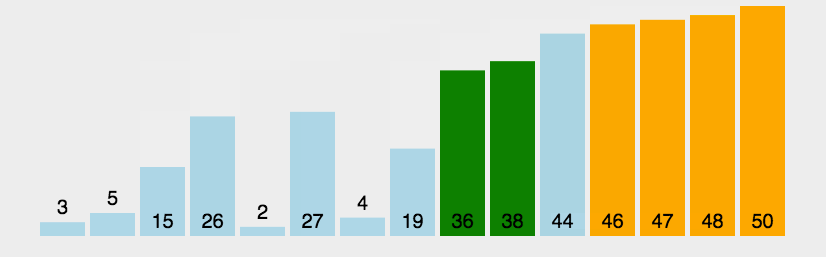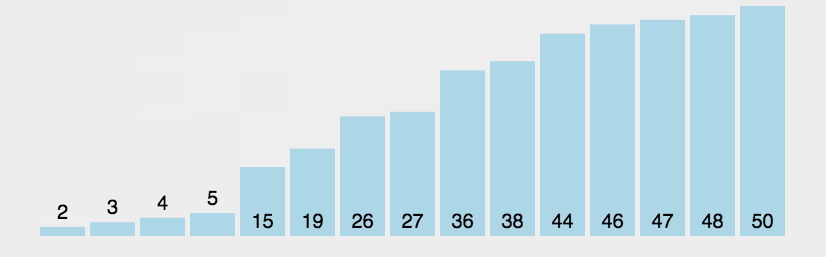
代码实现:
package aboutArraySort;
import java.util.Arrays;
public class BubbleSort {
public static void main(String[] args) {
int[] array = {37, 59, 43, -98, -17, 0};
sort(array);
System.out.println(Arrays.toString(array));
}
public static void sort(int[] array) {
for (int i = array.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (array[j] > array[j+1]) {
swapValue(array, j, j+1);
}
}
}
}
private static void swapValue(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
那么,本人来展示下运行结果:
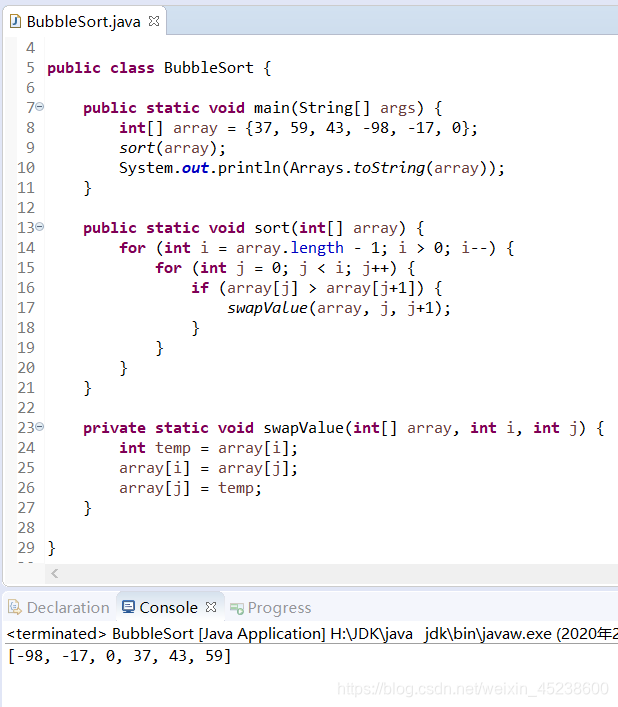
选择排序
时间复杂度:
O(n^2)
基本原理:
用未排序序列的第一个数和后面的所有数相比,
这样一轮下来,最大(或最小)的数就排到了相应的位置
经过最多(array.length - 1)轮后,整个数组就排好了序
动态演示:
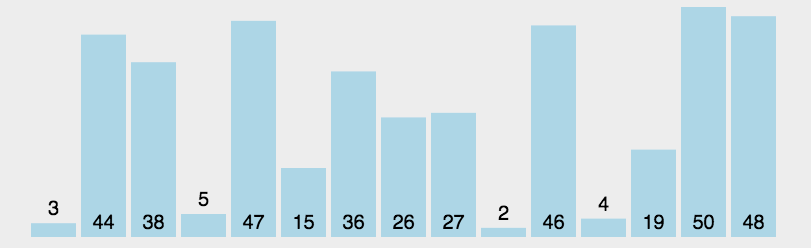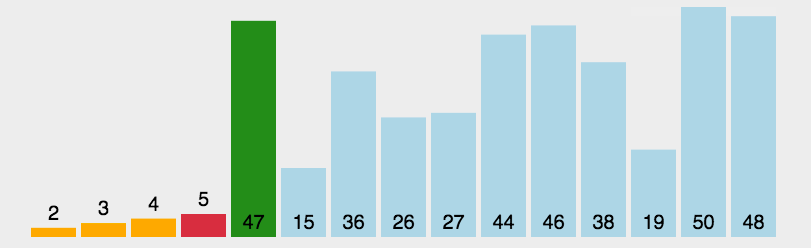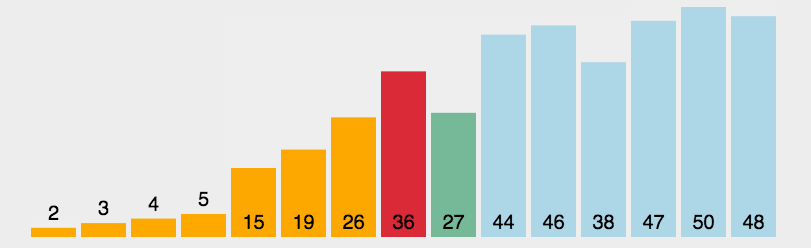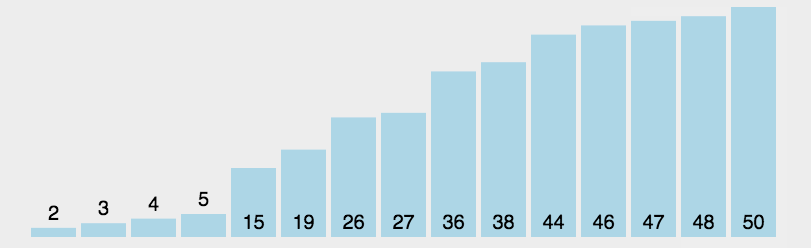
代码实现:
package aboutArraySort;
import java.util.Arrays;
public class SelectionSort {
public static void main(String[] args) {
int[] array = {37, 59, 43, -98, -17, 0};
sort(array);
System.out.println(Arrays.toString(array));
}
public static void sort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
for (int j = i+1; j < array.length; j++) {
if (array[i] > array[j]) {
swapValue(array, i, j);
}
}
}
}
private static void swapValue(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
那么,本人来展示下运行结果:
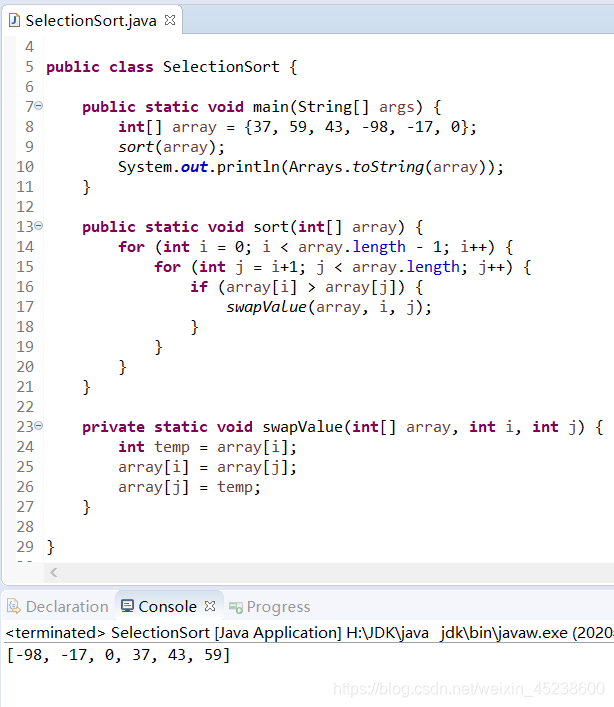
插入排序
时间复杂度:
O(n^2)
基本原理:
首先将原始数组分成两个数组容器(可通过下标来)
将原始数组的第一个数放在1号容器中,其余放在2号容器中
从2号容器中逐个取出,插在1号容器的适当位置
动态演示:
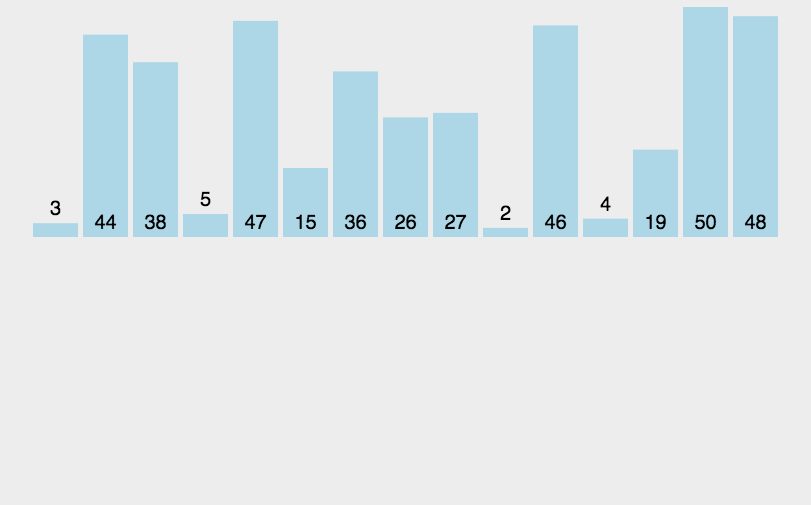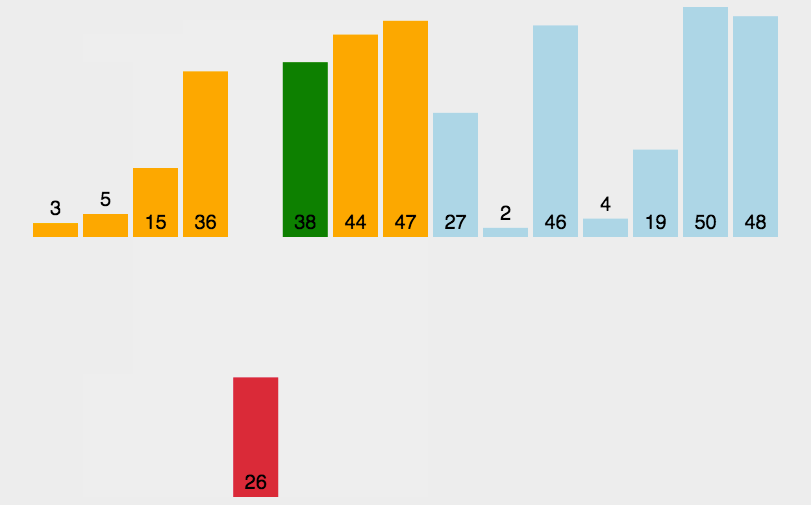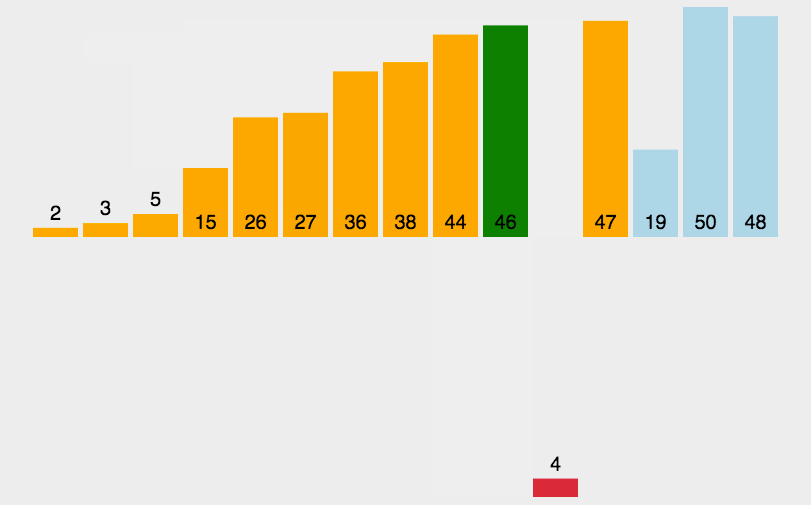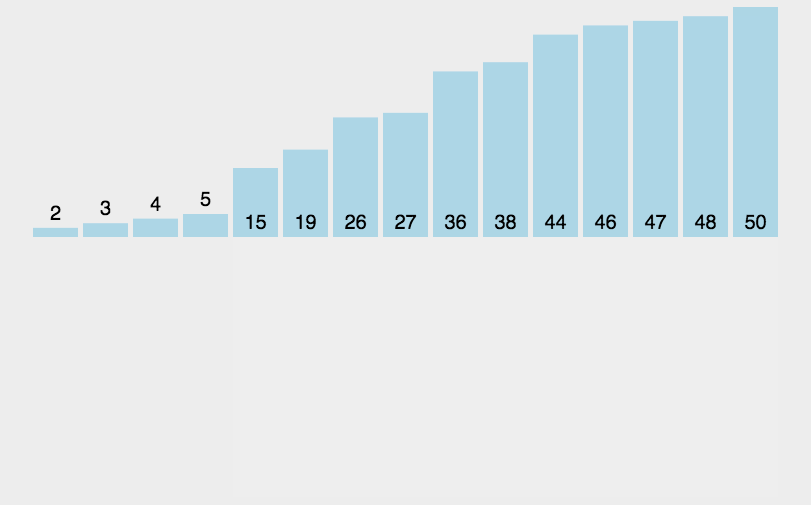
代码实现:
package aboutArraySort;
import java.util.Arrays;
public class InsertionSort {
public static void main(String[] args) {
int[] array = {37, 59, 43, -98, -17, 0};
sort(array);
System.out.println(Arrays.toString(array));
}
public static void sort(int[] array) {
for (int i = 0; i < array.length; i++) {
for (int j = i; j > 0; j--) {
if (array[j-1] > array[j]) {
swapValue(array, j-1, j);
}
}
}
}
private static void swapValue(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
那么,本人来展示下运行结果:
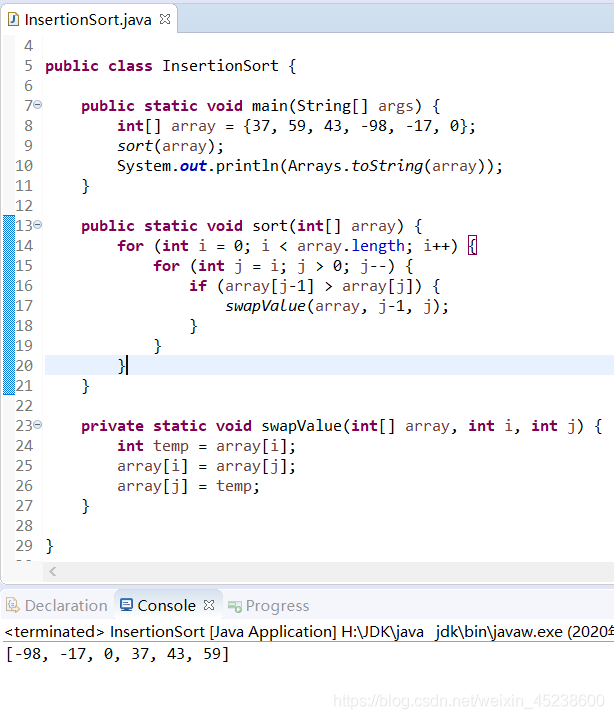
希尔排序
时间复杂度:
O(n^1.3)
基本原理:
先将原数组中的数据按照增量step分组
分出来的组按照插入排序进行排序
之后再对每个小组按照增量step/2分组
再对每个小组进行插入排序。
如此类推,直到增量step=1时,整个数组就排好序了
那么,看了上面的基本原理,我们就能知道 :
增量step的选取十分关键
所以,在这里,本人就用了克努特序列来计算增量step。
所谓克努特序列,
就是按照:num = num*3 + 1的顺序排列的序列
例:1, 4, 13, 40, 121, 364 ... ...
由数学推导可得:用这种序列来进行希尔排序,效率极高。
动态演示:

代码实现:
package aboutArraySort;
import java.util.Arrays;
public class ShellSort {
public static void main(String[] args) {
int[] array = {37, 59, 43, -98, -17, 0};
sort(array);
System.out.println(Arrays.toString(array));
}
public static void sort(int[] array) {
int maxStep = calculationStepLength(array.length);
for (int step = maxStep; step > 0; step = (step-1)/3) {
for (int i = step; i < array.length; i++) {
for (int j = i; j > step - 1; j -= step) {
if (array[j-step] > array[j]) {
swapValue(array, j, j - step);
}
}
}
}
}
private static int calculationStepLength(int length) {
int res = 1;
while (res < length / 3) {
res = res * 3 + 1;
}
return res;
}
private static void swapValue(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
那么,本人来展示下运行结果:
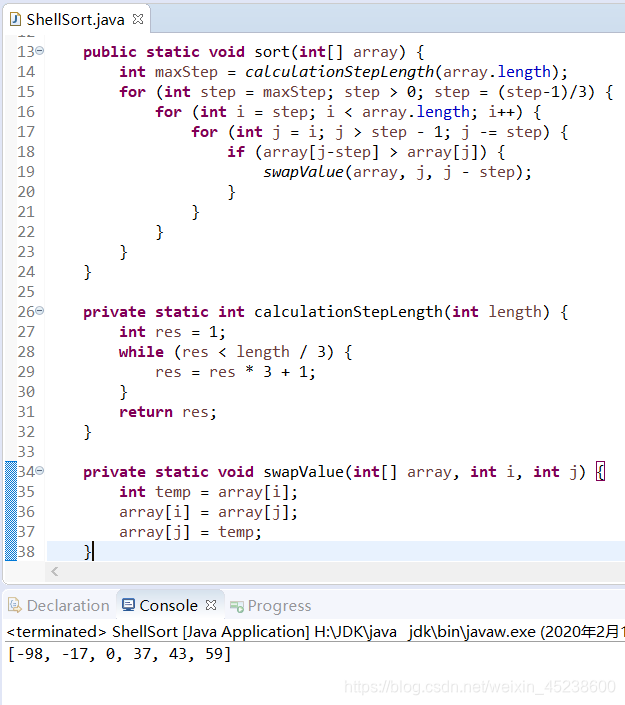
快速排序
时间复杂度:
O(nlog n)
基本原理:
首先选取数组中的第一个数作为基准数
然后将比它大的数放在它的左边,比它小的数放在右边
这样一来,这个基准数的位置就找好了
接下来,我们再对左右两个区间的数分别进行如上的操作
重复上面的所有操作,直到每个区间只有一个数为止
动态演示:
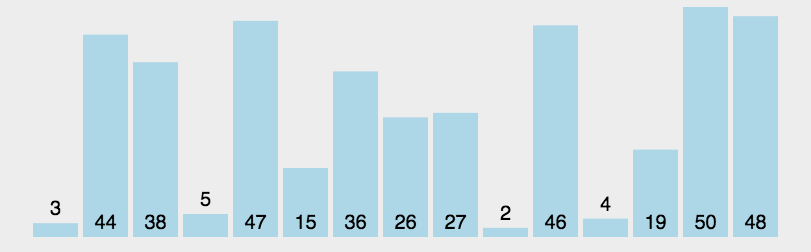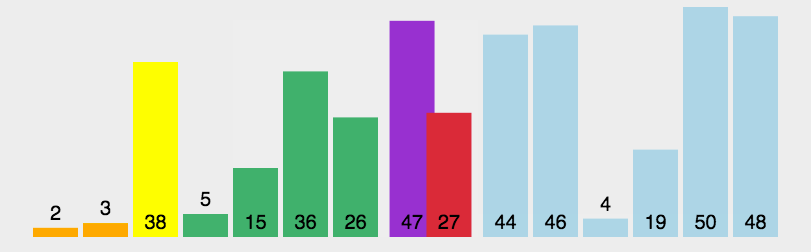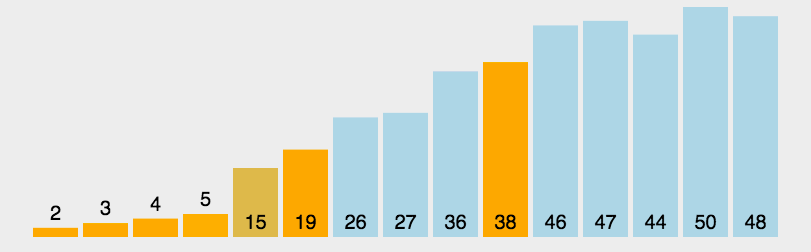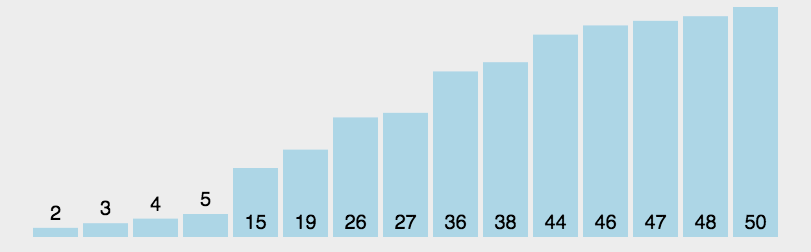
代码实现:
package aboutArraySort;
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] array = {37, 59, 43, -98, -17, 0};
sort(array);
System.out.println(Arrays.toString(array));
}
public static void sort(int[] array) {
qiuckSort(array, 0, array.length-1);
}
private static void qiuckSort(int[] array, int start, int end) {
if (start < end) {
int refIndex = getRefIndex(array, start, end);
qiuckSort(array, start, refIndex-1);
qiuckSort(array, refIndex+1, end);
}
}
private static int getRefIndex(int[] array, int start, int end) {
int i = start;
int j = end;
int temp = array[start];
while (i < j) {
while (i<j && (array[j]>=temp)) {
j--;
}
if (i < j) {
array[i] = array[j];
i++;
}
while (i<j && (array[i]<temp)) {
i++;
}
if (i < j) {
array[j] = array[i];
j--;
}
}
array[i] = temp;
return i;
}
}
那么,本人来展示下运行结果:

归并排序
时间复杂度:
O(nlog n)
基本原理:
假设一个数组是由length个有序数组组成的
然后两两排序
之后再将每两个数组元素看作是一个有序序列,再重复上面的步骤
直到将整个数组看作是一个有序序列,那么这个数组就已经排好序了
动态演示:
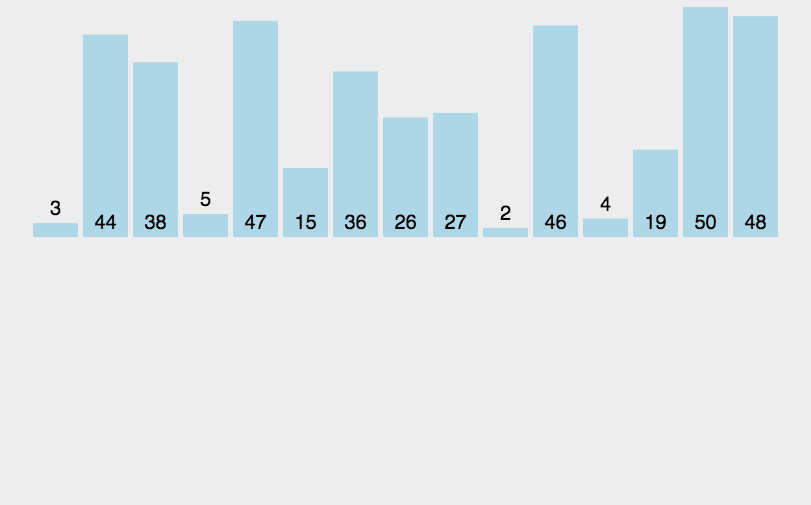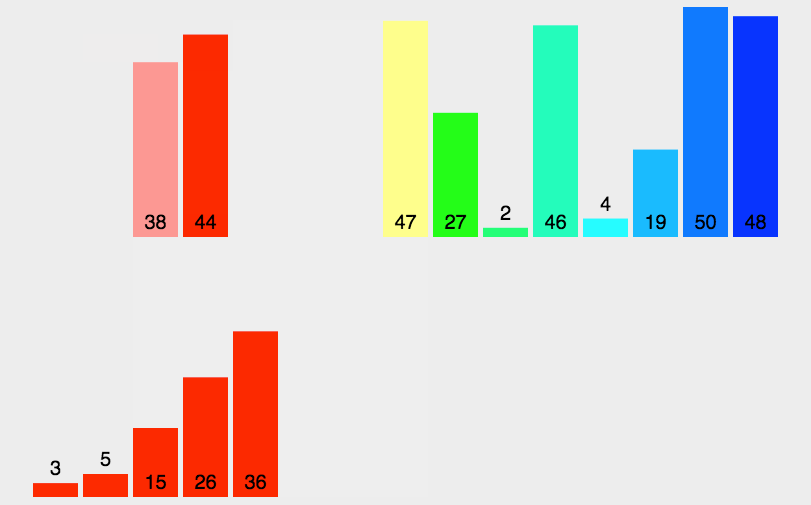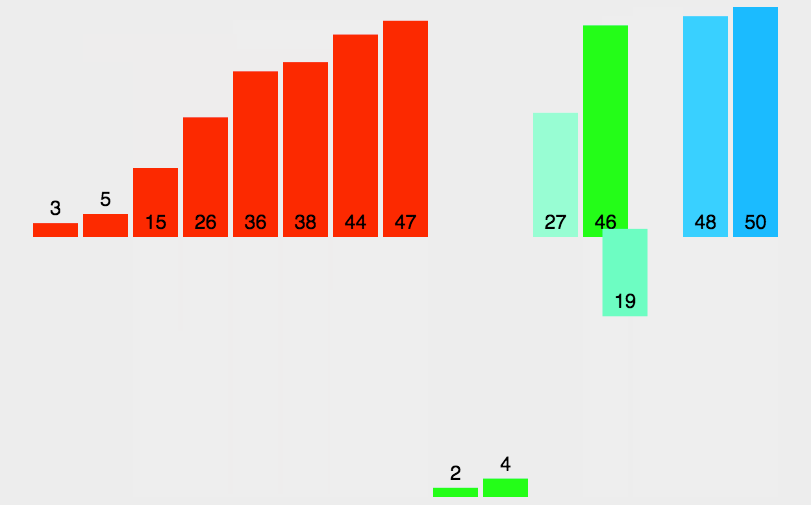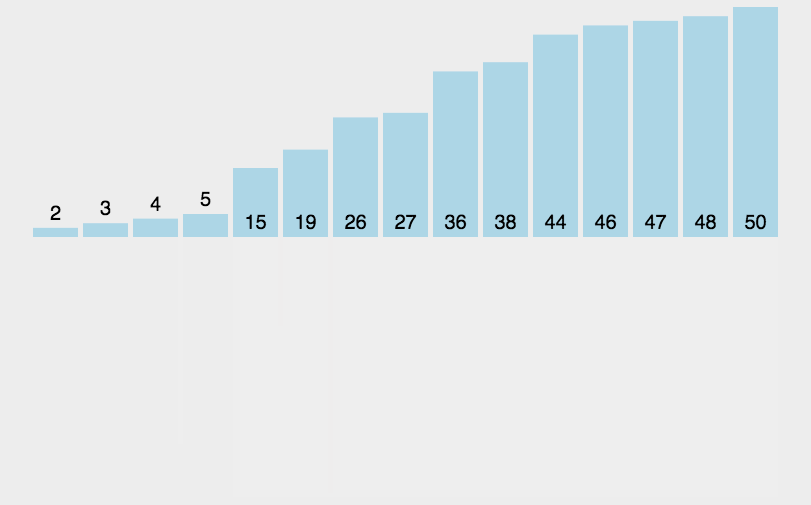
代码实现:
package aboutArraySort;
import java.util.Arrays;
public class MergeSort {
public static void main(String[] args) {
int[] array = {37, 59, 43, -98, -17, 0};
sort(array);
System.out.println(Arrays.toString(array));
}
public static void sort(int[] array) {
mergeSort(array, 0, array.length - 1);
}
private static void mergeSort(int[] array, int startIndex, int endIndex) {
int centerIndex = (endIndex + startIndex)/2;
if (startIndex < endIndex) {
mergeSort(array, startIndex, centerIndex);
mergeSort(array, centerIndex + 1, endIndex);
merge(array, startIndex ,endIndex);
}
}
/* 合并两个子数组 */
private static void merge(int[] array, int startIndex, int endIndex) {
int centerIndex = (endIndex + startIndex)/2;
int i = startIndex;
int j = centerIndex + 1;
int[] res = new int[endIndex - startIndex + 1];
int index = 0;
//向临时数组中存储元素
while ((i <= centerIndex) && (j <= endIndex)) {
if (array[i] <= array[j]) {
res[index++] = array[i++];
} else {
res[index++] = array[j++];
}
}
//处理剩余元素
while (i <= centerIndex) {
res[index++] = array[i++];
}
while (j <= endIndex) {
res[index++] = array[j++];
}
//将临时数组中的值转交给原数组
for (int k = 0; k < res.length; k++) {
array[k + startIndex] = res[k];
}
}
}
那么,本人来展示下运行结果:
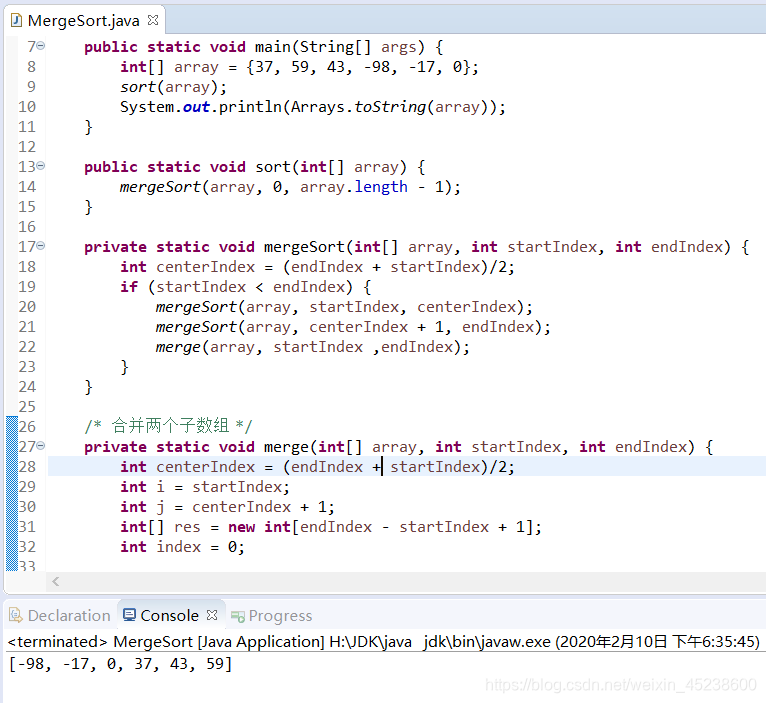
基数排序
时间复杂度:
O(d(r+n))
(d——长度
r —— 关键字基数
n ——关键字个数)
基本原理:
首先来建立编号为0~9的10个数组
然后将原数组中的每个元素通过个位的数值来存放在10个新数组对应的一个当中
然后再按照0~9的顺序将所有存入的数取出
再来按照原数组中的每个值的十位的值,来存放在10个新数组对应的一个当中
重复上面的操作,直到最高位也被这样比较了
等最后一次取出时,这个数组就排好序了
(由于我们设置的数组只能用于识别每一位的值,而不能识别正负,
所以,基数排序只能用于排列正数)
动态演示:

代码实现:
package aboutArraySort;
import java.util.Arrays;
public class RadixSort {
public static void main(String[] args) {
int[] array = {37, 59, 43, 0};
sort(array);
System.out.println(Arrays.toString(array));
}
public static void sort(int[] array) {
int[][] tempArray = new int[10][array.length];
int[] capacity = new int[10];
int max = getMax(array);
int maxLen = String.valueOf(max).length();
for (int i = 0, n = 1; i < maxLen; i++, n *= 10) {
for (int j = 0; j < array.length; j++) {
//取每轮相应的位的值
int remainder = array[j]/n%10;
tempArray[remainder][capacity[remainder]++] = array[j];
}
//取出临时数组中的元素
int index = 0;
for (int k = 0; k < capacity.length; k++) {
if (capacity[k] != 0) {
for (int x = 0; x < capacity[k]; x++) {
array[index++] = tempArray[k][x];
}
//清空临时数组中的记录,以便我们之后再次使用这个数组
capacity[k] = 0;
}
}
}
}
private static int getMax(int[] array) {
int res = array[0];
if (array.length < 2) {
return res;
}
for (int i = 1; i < array.length; i++) {
if (array[i] > res) {
res = array[i];
}
}
return res;
}
}
那么,本人来展示下运行结果:
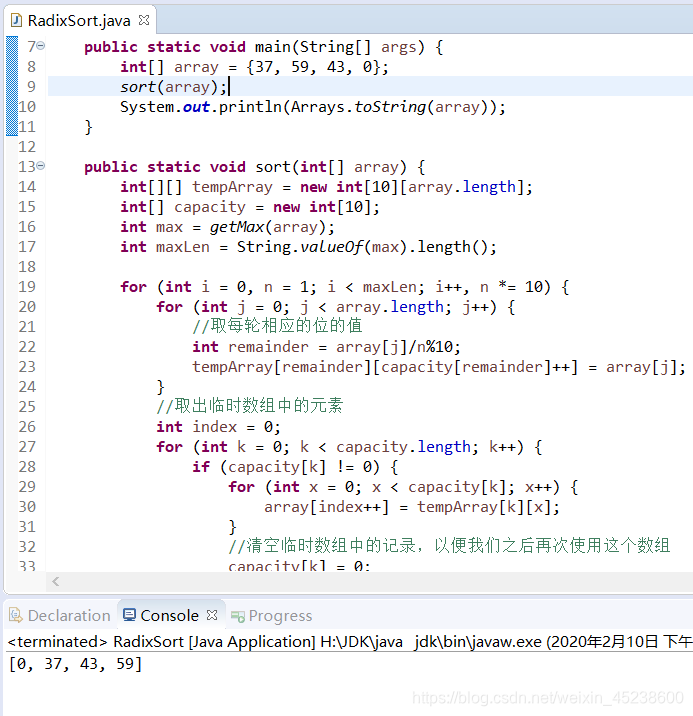
堆排序
时间复杂度:
O(nlog n)
基本原理:
首先将待排序列构造成一个大根堆,所以,此时的根节点就是整个数组的最大值
然后将根所存储的数值和末尾元素进行交换,这样一来,末尾元素就是本数组的最大值
之后将除末尾元素外的剩余元素再次转换为大根堆,反复进行上述的操作
待剩余最后一个元素时,这个数组就排序完成了
动态演示:
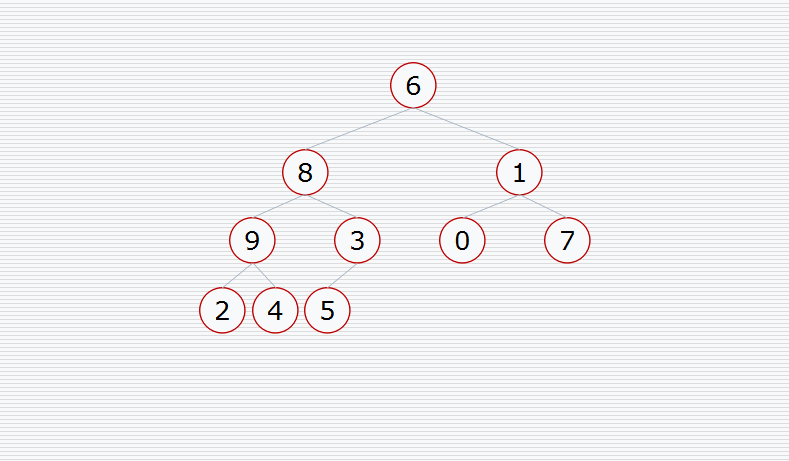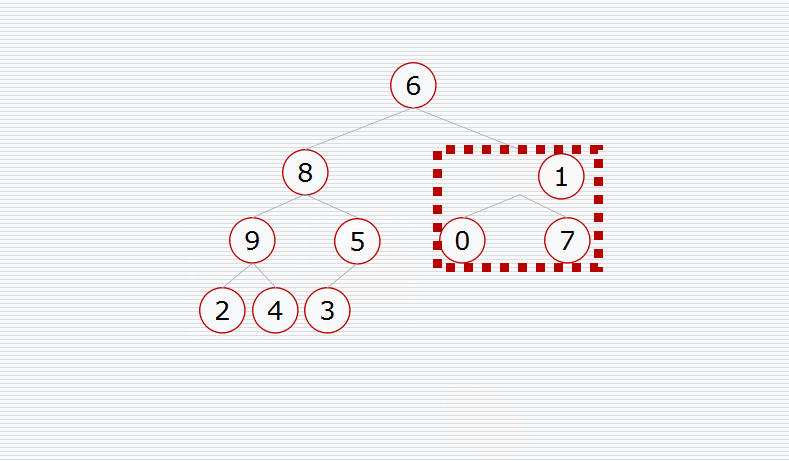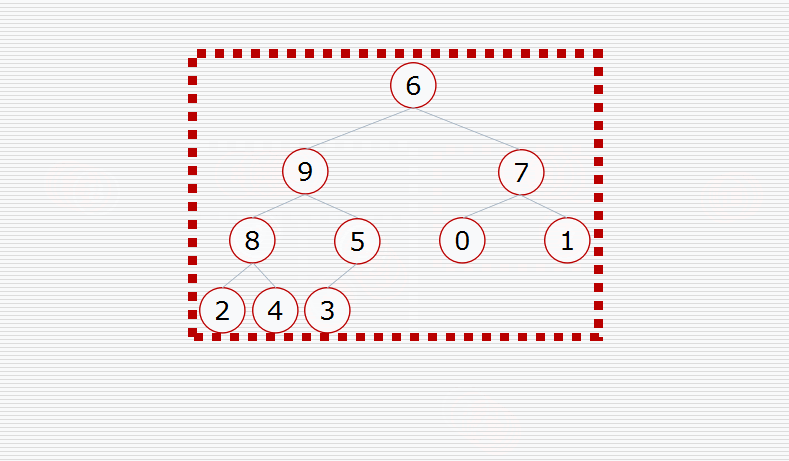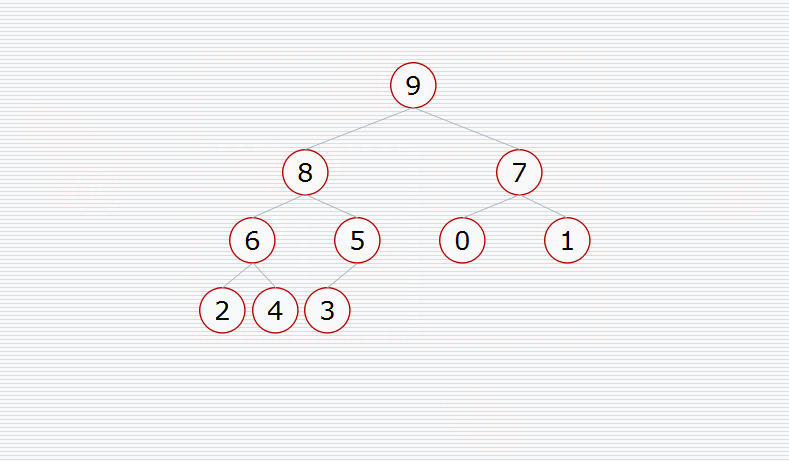
代码实现:
package aboutArraySort;
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] array = {37, 59, 43, -98, -17, 0};
sort(array);
System.out.println(Arrays.toString(array));
}
public static void sort(int[] array) {
for (int i = (array.length-1)/2; i >= 0; i--) {
toBigRootHeap(array, array.length, i);
}
for (int i = array.length-1; i > 0; i--) {
//进行调换
swapValue(array, i, 0);
//再将剩余元素调换成大顶堆
toBigRootHeap(array, i, 0);
}
}
private static void toBigRootHeap(int[] array, int size, int index) {
//获取左右孩子的下标
int leftChildIndex = index * 2 + 1;
int rightChildIndex = index * 2 + 2;
//获得此根与左右孩子中的最大值的下标
int maxIndex = index;
if ((leftChildIndex < size) && (array[leftChildIndex] > array[maxIndex])) {
maxIndex = leftChildIndex;
}
if ((rightChildIndex < size) && (array[rightChildIndex] > array[maxIndex])) {
maxIndex = rightChildIndex;
}
//交换这三个数值的位置,将此节点转换为“大根”
if (maxIndex != index) {
swapValue(array, index, maxIndex);
//排序底下的节点,防止调换完导致底下的节点无法形成大根堆
toBigRootHeap(array, size, maxIndex);
}
}
private static void swapValue(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
那么,本人来展示下运行结果:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号