表达式的处理(堆栈 的使用)
在我们使用电子产品进行数据的输入和处理时,我们输入的数据其实大多是字符串,之后计算机会对这些字符串进行一些处理,将字符串转换为我们所录入的数据,之后进行一系列的操作,完成我们所输入的指令。
那么,这么看来,将所输入的字符串转化为正确的类型的数据也是非常重要的一步。所以,我们今天就来实现一下“表达式的处理”
在之前的博文中本人也提到了堆栈的知识,如果没有学习过“堆栈”的知识的同学,建议了解一下。
若是急于了解的话,这里解释下用到的知识:堆栈的存储数据顺序——“先入后出”,即先存入堆栈内的数据比之后存入的数据从堆栈内取出的时候要晚一些,用图像形象地表示如下:

如这张图所示,入堆栈顺序为:A、B、C、D、E,则出堆栈的顺序为:E、D、C、B、A。
那么,进入正题,开始我们今天的《表达式处理》的代码编写吧!
和往常一样,我们先上手编写mec.h头文件,代码如下:
#ifndef _MEC_H_
#define _MEC_H_
typedef unsigned char boolean;
#define TRUE 1
#define FALSE 0
#define NOT_FOUND -1
#endif
因为我们要用到堆栈的处理方式,所以,在这章我就直接用本人之前的博文《堆栈 的实现》中的代码:
mecStack.h:
#ifndef _MEC_STACK_H_
#define _MEC_STACK_H_
#include "mec.h"
typedef struct MEC_STACK {
void **stack;
int capacity;
int top;
}MEC_STACK;
boolean initStack(MEC_STACK **stack, int capacity);
void destoryStack(MEC_STACK **stack);
boolean isStackEmpty(const MEC_STACK *stack);
boolean isStackFull(const MEC_STACK *stack);
boolean push(MEC_STACK *stack, void *data);
void *pop(MEC_STACK *stack);
void *readTop(const MEC_STACK *stack);
#endif
mecStack.c:
#include <stdio.h>
#include <malloc.h>
#include "mec.h"
#include "mecStack.h"
void *readTop(const MEC_STACK *stack) {
if (NULL == stack || isStackEmpty(stack)) {
return NULL;
}
return stack->stack[stack->top - 1];
}
void *pop(MEC_STACK *stack) {
if (NULL == stack || isStackEmpty(stack)) {
return NULL;
}
return stack->stack[--stack->top];
}
boolean push(MEC_STACK *stack, void *data) {
if (NULL == stack || isStackFull(stack)) {
return FALSE;
}
stack->stack[stack->top++] = data;
return TRUE;
}
boolean isStackFull(const MEC_STACK *stack) {
return stack != NULL && stack->top >= stack->capacity;
}
boolean isStackEmpty(const MEC_STACK *stack) {
return stack != NULL && stack->top <= 0;
}
void destoryStack(MEC_STACK **stack) {
if (NULL == stack || NULL == *stack) {
return;
}
free((*stack)->stack);
free(*stack);
*stack = NULL;
}
boolean initStack(MEC_STACK **stack, int capacity) {
MEC_STACK *res;
if (NULL == stack || NULL != *stack || capacity <= 0) {
return FALSE;
}
res = (MEC_STACK *) calloc(sizeof(MEC_STACK), 1);
res->stack = (void **) calloc(sizeof(void *), capacity);
res->capacity = capacity;
res->top = 0;
*stack = res;
return TRUE;
}
现在,我们存储数据的“堆栈”要用到的函数都准备好了,现在我们来整理一下大体的实现步骤,因为时表达式,所以会出现错误,那么,我们就来绘制下状态变迁图:
首先是处理单个数字:
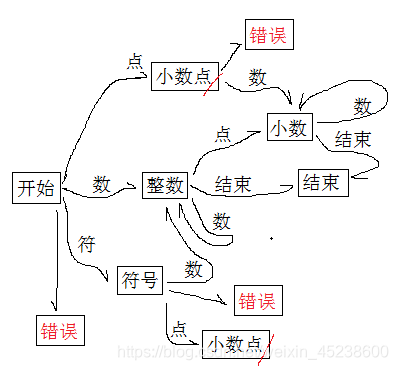
所以,相关代码如下:
首先,我们来构建一个表示“状态”的结构体:
typedef struct ARG {
boolean ok; //记录当前数字是否正确
boolean finished; //记录字符串是否结束
int status; //记录当前数字的状态
int i; //记录小数阶数
double value; //用于存储一个数的值
int sign; //记录符号
double pw; //用于将小数部分的数按照相应位数加到value成员的相应位上
}ARG;
是取数函数:
boolean getNumber(const char *str, double *result, int *count) {
ARG arg = {
TRUE, // boolean ok;
FALSE, // boolean finished;
NUMBER_STATUS_BEGIN, // int status;
0, // int i;
0.0, // double value;
1, // int sign;
0.1, // double pw;
};
while (arg.ok && !arg.finished) {
if (NUMBER_STATUS_BEGIN == arg.status) {
dealNumberStatusBegin(str[arg.i], &arg);
} else if (NUMBER_STATUS_SIGN == arg.status) {
dealNumberStatusSign(str[arg.i], &arg);
} else if (NUMBER_STATUS_DOT == arg.status) {
dealNumberStatusDot(str[arg.i], &arg);
} else if (NUMBER_STATUS_INTEGER == arg.status) {
dealNumberStatusInteger(str[arg.i], &arg);
} else if (NUMBER_STATUS_DECIMAL == arg.status) {
dealNumberStatusDecimal(str[arg.i], &arg);
} else if (NUMBER_STATUS_END == arg.status) {
*result = arg.sign == 1 ? arg.value : -arg.value;
*count = arg.i;
arg.finished = TRUE;
}
}
return arg.ok;
}
在上面的函数中,有很多处理其他状态的函数,代码如下:
void dealNumberStatusDecimal(int ch, ARG *arg) { //处理小数
if (isdigit(ch)) {
processDecimal(ch, arg);
arg->status = NUMBER_STATUS_DECIMAL;
arg->i++;
} else {
arg->status = NUMBER_STATUS_END;
}
}
void dealNumberStatusInteger(int ch, ARG *arg) { //处理整数
if ('.' == ch) {
arg->status = NUMBER_STATUS_DECIMAL;
arg->i++;
} else if (isdigit(ch)) {
processInteger(ch, arg);
arg->status = NUMBER_STATUS_INTEGER;
arg->i++;
} else {
arg->status = NUMBER_STATUS_END;
}
}
void dealNumberStatusDot(int ch, ARG *arg) { //处理小数点
if (isdigit(ch)) {
processDecimal(ch, arg);
arg->status = NUMBER_STATUS_DECIMAL;
arg->i++;
} else {
errMess = "数值不能只有“点”";
arg->ok = FALSE;
}
}
void dealNumberStatusSign(int ch, ARG *arg) { //处理符号
if (isdigit(ch)) {
processInteger(ch, arg);
arg->status = NUMBER_STATUS_INTEGER;
arg->i++;
} else if ('.' == ch) {
arg->status = NUMBER_STATUS_DOT;
arg->i++;
} else {
errMess = "缺少数字";
arg->ok = FALSE;
}
}
void dealNumberStatusBegin(int ch, ARG *arg) { //处理开始状态
if ('.' == ch) {
arg->status = NUMBER_STATUS_DOT;
arg->i++;
} else if ('+' == ch || '-' == ch) {
if ('-' == ch) {
arg->sign = -1;
}
arg->status = NUMBER_STATUS_SIGN;
arg->i++;
} else if (isdigit(ch)) {
processInteger(ch, arg);
arg->status = NUMBER_STATUS_INTEGER;
arg->i++;
} else {
errMess = "出师未捷身先死";
arg->ok = FALSE;
}
}
在以上的函数中,依然调用了两个函数,分别是产生整数的processInteger()和产生小数部分的processDecimal(),相关代码如下:
void processDecimal(int ch, ARG *arg) {
if (arg->pw < 1e-6) {
arg->ok = FALSE;
errMess = "小数位数超过6位";
return;
}
arg->value += arg->pw * (ch - '0');
arg->pw /= 10.0;
}
void processInteger(int ch, ARG *arg) {
arg->value = arg->value * 10 + (ch - '0');
}
之前的代码中我用到了好多errMess变量,这个变量是extern const char *类型,意味着是文件外部的变量
总结下,代码如下:
number.h:
#ifndef _NUMBER_H_
#define _NUMBER_H_
#include "mec.h"
#define NUMBER_STATUS_BEGIN 1
#define NUMBER_STATUS_END 2
#define NUMBER_STATUS_SIGN 3
#define NUMBER_STATUS_DOT 4
#define NUMBER_STATUS_INTEGER 5
#define NUMBER_STATUS_DECIMAL 6
boolean getNumber(const char *str, double *result, int *count);
#endif
number.c:
#include <stdio.h>
#include <ctype.h>
#include "mec.h"
#include "mecError.h"
#include "number.h"
extern const char *errMess;
typedef struct ARG {
boolean ok;
boolean finished;
int status;
int i;
double value;
int sign;
double pw;
}ARG;
static void dealNumberStatusBegin(int ch, ARG *arg);
static void dealNumberStatusSign(int ch, ARG *arg);
static void dealNumberStatusDot(int ch, ARG *arg);
static void dealNumberStatusInteger(int ch, ARG *arg);
static void dealNumberStatusDecimal(int ch, ARG *arg);
static void processInteger(int ch, ARG *arg);
static void processDecimal(int ch, ARG *arg);
static void processDecimal(int ch, ARG *arg) {
if (arg->pw < 1e-6) {
arg->ok = FALSE;
errMess = "小数位数超过6位";
return;
}
arg->value += arg->pw * (ch - '0');
arg->pw /= 10.0;
}
static void processInteger(int ch, ARG *arg) {
arg->value = arg->value * 10 + (ch - '0');
}
static void dealNumberStatusDecimal(int ch, ARG *arg) {
if (isdigit(ch)) {
processDecimal(ch, arg);
arg->status = NUMBER_STATUS_DECIMAL;
arg->i++;
} else {
arg->status = NUMBER_STATUS_END;
}
}
static void dealNumberStatusInteger(int ch, ARG *arg) {
if ('.' == ch) {
arg->status = NUMBER_STATUS_DECIMAL;
arg->i++;
} else if (isdigit(ch)) {
processInteger(ch, arg);
arg->status = NUMBER_STATUS_INTEGER;
arg->i++;
} else {
arg->status = NUMBER_STATUS_END;
}
}
static void dealNumberStatusDot(int ch, ARG *arg) {
if (isdigit(ch)) {
processDecimal(ch, arg);
arg->status = NUMBER_STATUS_DECIMAL;
arg->i++;
} else {
errMess = "数值不能只有“点”";
arg->ok = FALSE;
}
}
static void dealNumberStatusSign(int ch, ARG *arg) {
if (isdigit(ch)) {
processInteger(ch, arg);
arg->status = NUMBER_STATUS_INTEGER;
arg->i++;
} else if ('.' == ch) {
arg->status = NUMBER_STATUS_DOT;
arg->i++;
} else {
errMess = "缺少数字";
arg->ok = FALSE;
}
}
static void dealNumberStatusBegin(int ch, ARG *arg) {
if ('.' == ch) {
arg->status = NUMBER_STATUS_DOT;
arg->i++;
} else if ('+' == ch || '-' == ch) {
if ('-' == ch) {
arg->sign = -1;
}
arg->status = NUMBER_STATUS_SIGN;
arg->i++;
} else if (isdigit(ch)) {
processInteger(ch, arg);
arg->status = NUMBER_STATUS_INTEGER;
arg->i++;
} else {
errMess = "出师未捷身先死";
arg->ok = FALSE;
}
}
boolean getNumber(const char *str, double *result, int *count) {
ARG arg = {
TRUE,
FALSE,
NUMBER_STATUS_BEGIN,
0,
0.0,
1,
0.1,
};
while (arg.ok && !arg.finished) {
if (NUMBER_STATUS_BEGIN == arg.status) {
dealNumberStatusBegin(str[arg.i], &arg);
} else if (NUMBER_STATUS_SIGN == arg.status) {
dealNumberStatusSign(str[arg.i], &arg);
} else if (NUMBER_STATUS_DOT == arg.status) {
dealNumberStatusDot(str[arg.i], &arg);
} else if (NUMBER_STATUS_INTEGER == arg.status) {
dealNumberStatusInteger(str[arg.i], &arg);
} else if (NUMBER_STATUS_DECIMAL == arg.status) {
dealNumberStatusDecimal(str[arg.i], &arg);
} else if (NUMBER_STATUS_END == arg.status) {
*result = arg.sign == 1 ? arg.value : -arg.value;
*count = arg.i;
arg.finished = TRUE;
}
}
return arg.ok;
}
我们现在来编写一下处理数据错误的mecError.h和mecError.c文件:
mecError.h:
#ifndef _MEC_ERROR_H_
#define _MEC_ERROR_H_
void showError();
#endif
mecError.c:
#include <stdio.h>
#include "mecError.h"
const char *errMess;
void showError() {
if (NULL == errMess) {
printf("No Error!\n");
return;
}
printf("Error:%s\n", errMess);
}
接下来是考虑数字之间的运算的状态变迁图:
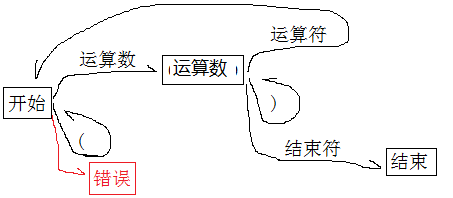
在上图中我们能够看出,我将遇到左括号的状态视为开始状态——即“栈空”状态,我们可以称之为“逻辑栈空”,因为我们现有的公认的数据处理方式中括号的优先级都是最高的,所以可以看作是“逻辑栈空”
由此可以看出一共有三种状态:开始,结束,运算
那么,我们现在来编写处理表达式的函数:
首先,我们模仿上述的状态图构建的结构体来构建一个结构体:
typedef struct ARGUMENT {
boolean ok;
boolean finished;
int status;
int index;
int bracketMatch; //用于处理括号匹配问题
MEC_STACK *operandStack; //这里的结构体指针的结构体就是我们最上面提到的实现堆栈所编写到的结构体
MEC_STACK *operatorStack;
}ARGUMENT;
现在,我们根据上面绘制的状态变迁图来编写分析表达式的函数;
boolean expressionParse(const char *str, double *value) {
ARGUMENT arg = {
TRUE, // boolean ok;
FALSE, // boolean finished;
EXPRESSION_STATUS_BEGIN, // int status;
0, // int index;
0, // int bracketMatch;
NULL, // MEC_STACK *operandStack;
NULL, // MEC_STACK *operatorStack;
};
int strLength = strlen(str);
double *res;
initStack(&arg.operandStack, strLength / 2 + 1); //这个函数我们在最上面的堆栈的代码中所编写
initStack(&arg.operatorStack, strLength / 2);
while (arg.ok && !arg.finished) { //这个循环中所提到的函数我们在下面逐一编写
arg.index += skipBlank(str + arg.index);
if (EXPRESSION_STATUS_BEGIN == arg.status) {
dealExpressionStatusBegin(str + arg.index, str[arg.index], &arg);
} else if (EXPRESSION_STATUS_OPERAND == arg.status) {
dealExpressionStatusOperand(str[arg.index], &arg);
} else if (EXPRESSION_STATUS_END == arg.status) {
if (!arg.ok) {
return FALSE;
}
if (arg.bracketMatch != 0) {
errMess = "(多余!";
return FALSE;
}
arg.finished = TRUE;
processOperator(NOT_OPERATOR, &arg);
res = (double *) pop(arg.operandStack);
*value = *res;
free(res);
}
}
destoryStack(&arg.operandStack);
destoryStack(&arg.operatorStack);
return arg.ok;
}
我们在这里来编写上面的函数的循环中所调用的函数:
首先是跳过空格函数:
int skipBlank(const char *str) {
int index;
for (index = 0; str[index] && isspace(str[index]); index++) {
;
}
return index;
}
接下来是处理表达式开始状态的函数:
void dealExpressionStatusBegin(const char *str, int ch, ARGUMENT *arg) {
int count;
double value;
double *operand;
int *leftBracket;
if (isNumber(ch)) {
arg->ok = getNumber(str, &value, &count);
if (!arg->ok) {
return;
}
arg->index += count;
operand = (double *) calloc(sizeof(double), 1);
*operand = value;
push(arg->operandStack, (void *) operand);
arg->status = EXPRESSION_STATUS_OPERAND;
} else if ('(' == ch) {
++arg->bracketMatch;
leftBracket = (int *) calloc(sizeof(int), 1);
*leftBracket = '(';
push(arg->operatorStack, leftBracket);
++arg->index;
arg->status = EXPRESSION_STATUS_BEGIN;
} else {
errMess = "非法表达式的开始";
arg->ok = FALSE;
}
}
上面的函数调用的getNumber()和push()函数均是上面编写的其他的文件中所编写的。
我们接下来编写上面的函数所调用的判断是否位运算数的函数:
boolean isNumber(int ch) {
return isdigit(ch) || '.' == ch || '+' == ch || '-' == ch;
}
现在,编写处理运算符的函数:
dealExpressionStatusOperand(int ch, ARGUMENT *arg) {
int *leftBracket;
if ((ch = isOperator(ch)) != NOT_OPERATOR) {
processOperator(ch, arg);
if (arg->ok) {
arg->index++;
arg->status = EXPRESSION_STATUS_BEGIN;
}
} else if (')' == ch) {
if (--arg->bracketMatch < 0) {
errMess = ")多余!";
arg->ok = FALSE;
return;
}
// 应该将运算符堆栈中下一个'('之前的所有运算符全部出栈并计算!
processOperator(NOT_OPERATOR, arg);
// 让后再将那个'('出栈!
leftBracket = pop(arg->operatorStack);
free(leftBracket);
arg->index++;
arg->status = EXPRESSION_STATUS_OPERAND;
} else {
arg->status = EXPRESSION_STATUS_END;
}
}
上面的判断符号函数(isOperator()函数)现在来编写:
int isOperator(int ch) {
int index;
for (index = 0; index < OPERATOR_COUNT; index++) {
if (ch == operatorList[index]) {
return index;
}
}
return NOT_OPERATOR;
}
现在我们来编写产生运算数的函数:
void processOperator(int oper, ARGUMENT *arg) {
int *cur;
int *pre;
int *topOper;
double *rightOperand;
double *leftOperand;
pre = (int *) readTop(arg->operatorStack);
while (arg->ok && !isStackLogicEmpty(arg->operatorStack)
&& (NOT_OPERATOR == oper || compareOperator(*pre, oper) == HIGH)) {
topOper = (int *) pop(arg->operatorStack);
rightOperand = (double *) pop(arg->operandStack);
leftOperand = (double *) pop(arg->operandStack);
arg->ok = compute(*topOper, leftOperand, *rightOperand);
if (!arg->ok) {
return;
}
free(rightOperand);
free(topOper);
push(arg->operandStack, leftOperand);
pre = (int *) readTop(arg->operatorStack);
}
if (arg->ok && NOT_OPERATOR != oper) {
cur = (int *) calloc(sizeof(int), 1);
*cur = oper;
push(arg->operatorStack, (void *) cur);
}
}
我们之前在处理状态变迁图时说过,遇到左括号,我们就当作“堆栈空栈”,即“逻辑栈空”,现在来编写判断逻辑栈空的函数:
boolean isStackLogicEmpty(const MEC_STACK *stack) {
int *topOper;
if (isStackEmpty(stack)) {
return TRUE;
}
topOper = (int *) readTop(stack);
return '(' == *topOper;
}
因为我们要编写运算表达式的函数的话,就要先知道运算数和运算符的优先级,而运算数的问题在上面的函数中已经实现了,那么,现在我们开始编写比较运算符优先级的函数:
这个函数就比较考察编程者的编程思维和编程能力了,本人的处理方式是建立一个二维数组,1,2,3,4,5分别当作+,-,*,/,^,数组中的元素分别表示横坐标表示的符号和纵坐标标识的符号比较优先级顺序,相关代码如下:
boolean operatorPriority[OPERATOR_COUNT][OPERATOR_COUNT] = {
// + - * / ^
/* + */ HIGH, HIGH, LOW, LOW, LOW,
/* - */ HIGH, HIGH, LOW, LOW, LOW,
/* * */ HIGH, HIGH, HIGH, HIGH, LOW,
/* / */ HIGH, HIGH, HIGH, HIGH, LOW,
/* ^ */ HIGH, HIGH, HIGH, HIGH, LOW,
};
boolean compareOperator(int pre, int cur) {
return operatorPriority[pre][cur];
}
那么我们现在编写运算函数:
boolean compute(int oper, double *left, double right) {
switch (operatorList[oper]) {
case '+':
*left += right;
break;
case '-':
*left -= right;
break;
case '*':
*left *= right;
break;
case '/':
if (fabs(right) <= 1e-6) {
errMess = "除0错!";
return FALSE;
}
*left /= right;
break;
case '^':
*left = pow(*left, right);
break;
}
return TRUE;
}
现在我们来总结下关于处理表达式所编写的.c和.h文件:
expression.h:
#ifndef _EXPRESSION_H_
#define _EXPRESSION_H_
#include "mec.h"
#define EXPRESSION_STATUS_BEGIN 1
#define EXPRESSION_STATUS_END 2
#define EXPRESSION_STATUS_OPERAND 3
boolean expressionParse(const char *str, double *value);
#endif
expression.c:
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <malloc.h>
#include <math.h>
#include "mec.h"
#include "mecError.h"
#include "expression.h"
#include "mecStack.h"
extern const char *errMess;
typedef struct ARGUMENT {
boolean ok;
boolean finished;
int status;
int index;
int bracketMatch;
MEC_STACK *operandStack;
MEC_STACK *operatorStack;
}ARGUMENT;
#define HIGH 1
#define LOW 2
#define NOT_OPERATOR -1
#define OPERATOR_COUNT 5
const char *operatorList = "+-*/^";
const boolean operatorPriority[OPERATOR_COUNT][OPERATOR_COUNT] = {
HIGH, HIGH, LOW, LOW, LOW,
HIGH, HIGH, LOW, LOW, LOW,
HIGH, HIGH, HIGH, HIGH, LOW,
HIGH, HIGH, HIGH, HIGH, LOW,
HIGH, HIGH, HIGH, HIGH, LOW,
};
static boolean isNumber(int ch);
static int skipBlank(const char *str);
static int isOperator(int ch);
static void dealExpressionStatusBegin(const char *str, int ch, ARGUMENT *arg);
static void dealExpressionStatusOperand(int ch, ARGUMENT *arg);
static void processOperator(int oper, ARGUMENT *arg);
static boolean compareOperator(int pre, int cur);
static boolean compute(int oper, double *left, double right);
static boolean isStackLogicEmpty(const MEC_STACK *stack);
static boolean isStackLogicEmpty(const MEC_STACK *stack) {
int *topOper;
if (isStackEmpty(stack)) {
return TRUE;
}
topOper = (int *) readTop(stack);
return '(' == *topOper;
}
static boolean compute(int oper, double *left, double right) {
switch (operatorList[oper]) {
case '+':
*left += right;
break;
case '-':
*left -= right;
break;
case '*':
*left *= right;
break;
case '/':
if (fabs(right) <= 1e-6) {
errMess = "除0错!";
return FALSE;
}
*left /= right;
break;
case '^':
*left = pow(*left, right);
break;
}
return TRUE;
}
static boolean compareOperator(int pre, int cur) {
return operatorPriority[pre][cur];
}
static void processOperator(int oper, ARGUMENT *arg) {
int *cur;
int *pre;
int *topOper;
double *rightOperand;
double *leftOperand;
pre = (int *) readTop(arg->operatorStack);
while (arg->ok && !isStackLogicEmpty(arg->operatorStack)
&& (NOT_OPERATOR == oper || compareOperator(*pre, oper) == HIGH)) {
topOper = (int *) pop(arg->operatorStack);
rightOperand = (double *) pop(arg->operandStack);
leftOperand = (double *) pop(arg->operandStack);
arg->ok = compute(*topOper, leftOperand, *rightOperand);
if (!arg->ok) {
return;
}
free(rightOperand);
free(topOper);
push(arg->operandStack, leftOperand);
pre = (int *) readTop(arg->operatorStack);
}
if (arg->ok && NOT_OPERATOR != oper) {
cur = (int *) calloc(sizeof(int), 1);
*cur = oper;
push(arg->operatorStack, (void *) cur);
}
}
static void dealExpressionStatusOperand(int ch, ARGUMENT *arg) {
int *leftBracket;
if ((ch = isOperator(ch)) != NOT_OPERATOR) {
processOperator(ch, arg);
if (arg->ok) {
arg->index++;
arg->status = EXPRESSION_STATUS_BEGIN;
}
} else if (')' == ch) {
if (--arg->bracketMatch < 0) {
errMess = ")多余!";
arg->ok = FALSE;
return;
}
// 应该将运算符堆栈中下一个'('之前的所有运算符全部出栈并计算!
processOperator(NOT_OPERATOR, arg);
// 让后再将那个'('出栈!
leftBracket = pop(arg->operatorStack);
free(leftBracket);
arg->index++;
arg->status = EXPRESSION_STATUS_OPERAND;
} else {
arg->status = EXPRESSION_STATUS_END;
}
}
static void dealExpressionStatusBegin(const char *str, int ch, ARGUMENT *arg) {
int count;
double value;
double *operand;
int *leftBracket;
if (isNumber(ch)) {
arg->ok = getNumber(str, &value, &count);
if (!arg->ok) {
return;
}
arg->index += count;
operand = (double *) calloc(sizeof(double), 1);
*operand = value;
push(arg->operandStack, (void *) operand);
arg->status = EXPRESSION_STATUS_OPERAND;
} else if ('(' == ch) {
++arg->bracketMatch;
leftBracket = (int *) calloc(sizeof(int), 1);
*leftBracket = '(';
push(arg->operatorStack, leftBracket);
++arg->index;
arg->status = EXPRESSION_STATUS_BEGIN;
} else {
errMess = "非法表达式的开始";
arg->ok = FALSE;
}
}
static int isOperator(int ch) {
int index;
for (index = 0; index < OPERATOR_COUNT; index++) {
if (ch == operatorList[index]) {
return index;
}
}
return NOT_OPERATOR;
}
static int skipBlank(const char *str) {
int index;
for (index = 0; str[index] && isspace(str[index]); index++) {
;
}
return index;
}
boolean expressionParse(const char *str, double *value) {
ARGUMENT arg = {
TRUE, // boolean ok;
FALSE, // boolean finished;
EXPRESSION_STATUS_BEGIN, // int status;
0, // int index;
0, // int bracketMatch;
NULL, // MEC_STACK *operandStack;
NULL, // MEC_STACK *operatorStack;
};
int strLength = strlen(str);
double *res;
initStack(&arg.operandStack, strLength / 2 + 1);
initStack(&arg.operatorStack, strLength / 2);
while (arg.ok && !arg.finished) {
arg.index += skipBlank(str + arg.index);
if (EXPRESSION_STATUS_BEGIN == arg.status) {
dealExpressionStatusBegin(str + arg.index, str[arg.index], &arg);
} else if (EXPRESSION_STATUS_OPERAND == arg.status) {
dealExpressionStatusOperand(str[arg.index], &arg);
} else if (EXPRESSION_STATUS_END == arg.status) {
if (!arg.ok) {
return FALSE;
}
if (arg.bracketMatch != 0) {
errMess = "(多余!";
return FALSE;
}
arg.finished = TRUE;
processOperator(NOT_OPERATOR, &arg);
res = (double *) pop(arg.operandStack);
*value = *res;
free(res);
}
}
destoryStack(&arg.operandStack);
destoryStack(&arg.operatorStack);
return arg.ok;
}
boolean isNumber(int ch) {
return isdigit(ch) || '.' == ch || '+' == ch || '-' == ch;
}
现在,我们的工具函数都做好了,我们在使用的时候只需用命令行编译或者虚拟机进行多文件联编即可!!!
这就是我们这篇《表达式的处理》博文所要讲解的所有内容了。
总之,还是建议先观看本人的另一篇博文《堆栈 的实现》,这样在观看这篇博文时就会容易些。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号