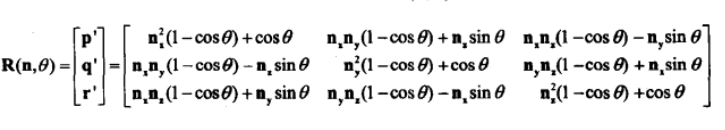[3D数学]矩阵 2017.8.16
<1>有时候我们想对整个物体做一定量旋转,其实可以直接对物体坐标系进行相反量的旋转
比如:现在想对一个物体顺时针旋转20度,再扩大200%,,既可以对这个物体的坐标系先缩小200%,再逆时针旋转20度: 注意这里组合变换,需要以相反的顺序做变换
<2>如何看出一个矩阵的旋转缩放?
从矩阵中抽出基向量,2维抽出的X,Y;2维矩阵在笛卡尔坐标系中呈现出一个"L"型,从这个“L”型中我们可以看出乘以这个矩阵的旋转 缩放效果:
比如:现在有矩阵 ,行向量A[1,0]乘以这个矩阵,得到的值会发生什么变化呢?AM = 1X2 2X2 = 1X2 = [2,1],新的行向量[2,1]相对于[1,0]做了什么变化呢?可以计算一下它们的夹角26.5度,缩放sqrt(5)
,行向量A[1,0]乘以这个矩阵,得到的值会发生什么变化呢?AM = 1X2 2X2 = 1X2 = [2,1],新的行向量[2,1]相对于[1,0]做了什么变化呢?可以计算一下它们的夹角26.5度,缩放sqrt(5)
3维矩阵中抽出基向量,X,Y,Z;3维矩阵呈现出一个“三脚架”形状,从这个“三脚架”形状可以看出乘以这个矩阵的旋转 缩放效果
<3>2D旋转矩阵:限制了位移 绕原点旋转
[cosθ sinθ]
[-sinθ cosθ]
对一个向量(4,2)旋转θ度 (4*cosθ-2*sinθ,4*sinθ+2*cosθ) 即为旋转θ度后的向量
<4>3D旋转矩阵:
3D旋转矩阵是绕着一条轴做旋转,可以不是笛卡尔坐标系的X,Y,Z轴,现在不考虑平移,只讨论旋转轴穿过原点的情况
下面列出旋转3条轴的公式:X,Y,Z


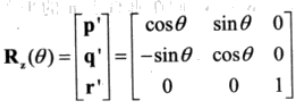
这三个旋转矩阵也很好记:X,Y,Z轴的旋转矩阵分别在1,2,3行写上单位基向量,在单位1的对角都写上0,剩下的4格子填上2维旋转矩阵
当一个3D物体旋转复杂的时候,我们可以拆分成多次绕轴旋转
绕任意轴旋转公式: