[2016北京集训测试赛7]isn-[树状数组+dp+容斥]

Description

 

Solution

定义dp[i][j]为在1到i个数中选了j个数，并且保证选了i的选法总数。

dp[i][j]为所有满足A[k]>A[i]的k(k<i)的dp[k][j-1]之和。在处理完dp[i][j]后，在树状数组里A[i]位置填上dp[i][j-1]的值就好。这样可以优化一下复杂度。[A可能要离散化一下]

然后，容斥大法好~

定义g[x]为最终序列长度为x的方案数。由于x是从大变小，所有的g[i]都是已经处理完毕的了。

（似乎还有一种不用n²操作，直接扫一遍就好的方法，不知道是不是二项式反演）

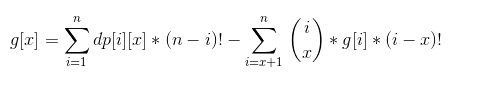
Code

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int mod=1e9+7;
typedef long long ll;
int n,a[2010],t[2010],rk[2010];
bool cmp(int x,int y){return a[x]<a[y];}
ll dp[2010][2010],g[2010];


ll fac[2010],inv[2010];
void pre()
{
    fac[0]=fac[1]=inv[0]=inv[1]=1;
    for (int i=2;i<=n;i++)
    {
        fac[i]=fac[i-1]*i%mod;
        inv[i]=(mod-mod/i)*inv[mod%i]%mod;
    }
    for (int i=2;i<=n;i++) inv[i]=inv[i]*inv[i-1]%mod;
}
ll C(int x,int y){return fac[y]*inv[x]%mod*inv[y-x]%mod;}


ll tree[2010];
void add(int id,ll x){for(;id<=n;id+=id&-id) tree[id]+=x,tree[id]%=mod;}
ll query(int id){ll re=0;for(;id;id-=id&-id) re+=tree[id],re%=mod;return re;}
int main()
{
    scanf("%d",&n);
    pre();
    for (int i=1;i<=n;i++) 
    {
        scanf("%d",&a[i]);t[i]=i;
    }
    sort(t+1,t+n+1,cmp);
    int js=0;
    a[0]=-1;
    for (int i=1;i<=n;i++) 
    {
        if (a[t[i]]!=a[t[i-1]]) js++;
        rk[t[i]]=js;
    }
    for (int i=1;i<=n;i++) dp[i][1]=1;
    for (int j=2;j<=n;j++) 
    {
        memset(tree,0,sizeof(tree));
        add(rk[j-1],dp[j-1][j-1]);
        for (int i=j;i<=n;i++)
        {
            dp[i][j]=query(rk[i]);
            add(rk[i],dp[i][j-1]);
        }        
    }

    g[n]=dp[n][n];
    for (int i=n-1;i;i--)
    {
        for (int j=1;j<=n;j++) g[i]+=dp[j][i]*fac[n-i]%mod,g[i]%=mod;
        for (int j=i+1;j<=n;j++) 
            g[i]-=C(i,j)*g[j]%mod*fac[j-i]%mod,g[i]%=mod;
    }
    ll ans=0;
    for (int i=1;i<=n;i++) ans=(ans+g[i]+mod)%mod;
    cout<<ans;
}