[agc006D]Median Pyramid Hard-[二分+乱搞]

Description

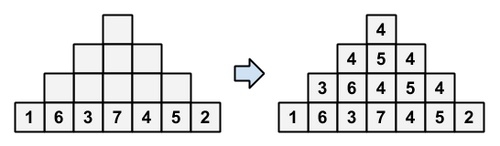
题目大意：给你一个长度为n*2-1的排列，将除了该序列头尾的两个数外的其他数（设为i）变为原序列i-1,i,i+1下标数的中位数。求最后的数是什么。例子如下：

　　　　　　　　

 

Solution

这道题我们考虑二分（反正我YY了好久也没想出其他做法）。

我们设当前二分到k，要判断答案与k的大小关系。将原排列中<=k的数设为0，反之设为1。

如此我们可以得到一个01序列。

通过分析可得，假如01序列中有两个相邻的数相等，则它们正上方的所有数都与它们相等。（我们可以称之为柱子）

         1    

      _ 1 1 

   _ _ 1 1 _ 

_ _ _ 1 1 _ _

则对于某个排列如果它最上方的数为0，有以下情况：

1，它的第n位是柱子。

2，以它的第n位为中心，左边或者右边只有为0的柱子

3，以它的第n位为中心，两边最近的柱子都为0

4，以它的第n位为中心，两边的柱子分别为0和1，但是0柱子离中心较近。

5，以它的第n位为中心，左右两边都没有柱子，则需要序列第1位为0。

以下为情况4的证明：

1|  1 1 1 1 1 0 0 0 0 0  |0

1|  1 1 1 1 1 0 0 0 0 0  |0

1|  1 1 1 1 0 1 0 0 0 0  |0

1|  1 1 1 0 1 0 1 0 0 0  |0

1|  1 1 0 1 0 1 0 1 0 0  |0

1|  1 0 1 0 1 0 1 0 1 0  |0

1|  0 1 0 1 0 1 0 1 0 1  |0

该图左边是1柱子，右边是0柱子。依图可证明。

其他证明同理。

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int n,a[400010],l,r,mid,ans;
bool _get(int x){ return !(x<=mid);}
bool check()
{
    for (int i=1;i<=n-1;i++)
    {
        if (_get(a[n+i-1])==_get(a[n+i])) return _get(a[n+i]);
        if (_get(a[n-i+1])==_get(a[n-i])) return _get(a[n-i+1]);
    }
    return _get(a[1]);
}
int main()
{
    scanf("%d",&n);
    for (int i=1;i<=2*n-1;i++) scanf("%d",&a[i]);
    l=1;r=2*n-1;
    while (l<=r)
    {
        mid=(l+r)/2;
        if (!check()) r=mid-1,ans=mid;else l=mid+1;
    }
    cout<<ans;
}