同时寻找最大数和最小数的最优算法
我们知道,在一个容量为n的数据集合中寻找一个最大数,不管用什么样的比较算法,至少要比较n-1次,就算是用竞标赛排序也得比较n-1次,否则你找到的就不能保证是最大的数。那么,在一个容量为n的数据集合中同时寻找最大数和最小数的最小比较次数是多少呢?
从一个容量为n的数据集合中同时找到最大数和最小数的最优方法是:首先让所有的元素参与两两比较,这样总共比较了n/2次,最大数肯定在胜者组中,最小数肯定在败者组中;然后从容量为n/2的胜者组中找到最大的数,最少要比较n/2 - 1次;同理,从容量为n/2的败者组中找到最小的数,最少要比较n/2 - 1次。所以总共需要比较(3n/2) - 2 次。以上假设n为偶数。奇数同理。
这是同时寻找最大数和最小数的最优算法。
那么,我们要从一个容量为n的数据集(假设该数据集是一个集合,即没有相同的元素)中找到第二大元素需要多少次比较呢?
一种习惯的方法是:先找出最大的元素,这需要比较n-1次;然后从剩下的n-1个元素中找到最大的,这个元素就是我们要找的第二大元素,这需要比较n-2次。做一总共比较2n-3次。
但是,
还有一个更优的方法:
(1) 我们考虑淘汰赛的比较法,淘汰赛结束后,找出冠军我们需要n-1次比较;如下图所示,找到12需要比较7次。
(2) 此时我们要考虑到,亚军应该存在于败给冠军的这些选手中(否则,每个元素都至少有两个元素比它大),由于与冠军比过的元素个数为┌log2n┐,从这些元素中找到最大值需要比较┌log2n┐ - 1次;如下图所示,亚军应该在10,11,4这三个元素中。否则,如果亚军是5,那么冠军12比它大,与它比较过的10也比它大,至少两个元素大于5,所以5肯定不是亚军的候选者。
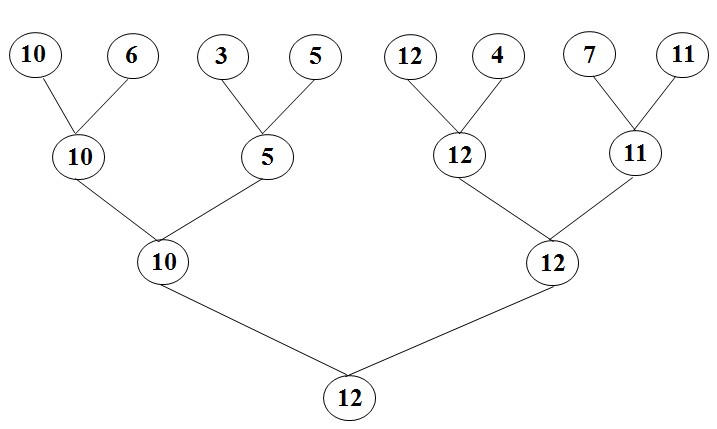
(3)从而找出亚军要比较n-1+┌log2n┐-1 = n-2+┌log2n┐次比较。这个算法是寻找亚军的最优算法。



