Leetcode 5304. 子数组异或查询
5304. 子数组异或查询
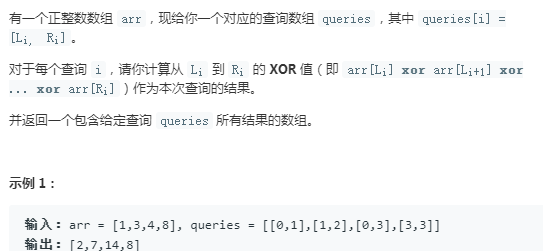
分析:
方法1:暴力求解:每次循环,从到Li到Ri的异或和,存入vector并返回;这种方法无疑会超时;
1 class Solution { 2 public: 3 vector<int> xorQueries(vector<int>& arr, vector<vector<int>>& queries) { 4 vector<int> res; 5 vector<vector<int>> dp; 6 vector<int> level; 7 int len=arr.size(); 8 int count; 9 //循环找 10 for(int i=0;i<queries.size();i++) 11 { 12 count=0; 13 int x = queries[i][0]>queries[i][1]?queries[i][1]:queries[i][0]; 14 int y = queries[i][0]>queries[i][1]?queries[i][0]:queries[i][1]; 15 for(int i=x;i<=y;i++) 16 { 17 count^=arr[i]; 18 } 19 res.push_back(count); 20 } 21 22 return res; 23 } 24 };
方法2:二维数组:dp[i][j]表示从i到j的异或和,dp[i][j]=dp[i][j-1] ^ arr[j];当数字的个数为n时,需要开辟n*n的空间,并且浪费掉了1/2的空间,因为dp[i][j]=dp[j][i];
1 class Solution { 2 public: 3 vector<int> xorQueries(vector<int>& arr, vector<vector<int>>& queries) { 4 vector<int> res; 5 vector<vector<int>> dp; 6 int len=arr.size(); 7 dp.resize(len,arr); //初始化 8 for(int i=0;i<len;i++) 9 { 10 for(int j=i;j<len;j++) 11 { 12 //填充dp数组dp[i][j]表示从i到j异或的结果 13 if(i==j) 14 dp[i][j]=arr[i]; 15 else 16 dp[i][j]=dp[i][j-1]^arr[j]; 17 } 18 } 19 20 //循环找 21 for(int i=0;i<queries.size();i++) 22 { 23 //int x = queries[i][0]>queries[i][1]?queries[i][1]:queries[i][0]; 24 //int y = queries[i][0]>queries[i][1]?queries[i][0]:queries[i][1]; 25 res.push_back(dp[queries[i][0]]queries[i][1]]); 26 } 27 28 return res; 29 } 30 };
方法3:在方法2的基础上,砍掉一半空间,但是结果还是超出了空间的最大消耗;
1 class Solution { 2 public: 3 vector<int> xorQueries(vector<int>& arr, vector<vector<int>>& queries) { 4 vector<int> res; 5 vector<vector<int>> dp; 6 vector<int> level; 7 int len=arr.size(); 8 for(int i=0;i<len;i++) 9 { 10 level.resize(len-i,0); 11 for(int j=0;j<len-i;j++) 12 { 13 //填充dp数组dp[i][j]表示从i到j异或的结果 14 if(j==0) 15 level[j]=arr[j+i]; 16 else 17 level[j]=level[j-1]^arr[j+i]; 18 } 19 dp.push_back(level); 20 } 21 22 //循环找 23 for(int i=0;i<queries.size();i++) 24 { 25 int x = queries[i][0]>queries[i][1]?queries[i][1]:queries[i][0]; 26 int y = queries[i][0]>queries[i][1]?queries[i][0]:queries[i][1]; 27 res.push_back(dp[x][y-x]); 28 } 29 30 return res; 31 } 32 };
方法4:看了题解,才知道还能这么算,直接保留前Ri项的异或和,然后再和前Li项的异或和做异或操作,相同的前Li项就被抵消掉了,空间消耗直接变成了n。
1 class Solution { 2 public: 3 vector<int> xorQueries(vector<int>& arr, vector<vector<int>>& queries) { 4 vector<int> dp; 5 dp.resize(arr.size(),0); 6 dp[0]=arr[0]; 7 for(int i=1;i<arr.size();i++) 8 { 9 dp[i]=dp[i-1]^arr[i]; 10 } 11 12 vector<int> res; 13 for(int i=0;i<queries.size();i++) 14 { 15 int l=queries[i][0]; 16 int r=queries[i][1]; 17 int num=(l==0)?dp[r]:(dp[r]^dp[l-1]); 18 res.push_back(num); 19 } 20 return res; 21 } 22 };



