重建二叉树

二叉树的遍历方式有4种：先序遍历，中序遍历，后序遍历以及层次遍历

根据中序遍历和另外任意一种遍历方式都可以唯一的重建二叉树！

如果没有中序遍历，其余任意两种组合均无法实现二叉树的重建，为什么？

其实原因很简单，先中后说的均为根结点的顺序，那么左子树一定先于右子树遍历到，中序遍历可以根据根结点，将左右子树分开！

那么如何根据中序遍历和后序遍历，重建出二叉树？

思路：假设递归过程中，某一步的后序序列区间为[postL,postR]，中序序列区间为[inL,inR]；

    1. 根据后序遍历的特点可知，postR位置为根结点；

    2. 从中序序列中，寻找出root的位置k，k左边的均为左子树，右边的均为右子树；

    3. 将左子树区间[postL,k-1]作为新的后序和中序序列，进行递归。

代码如下:

/*
 * 给定一个二叉树的后序遍历和中序遍历，重建这个二叉树
 */
/*
 * 思路：根据后序遍历找到根结点，根据中序遍历，根结点左边为左子树，根结点右边为右子树
 * 边界条件：后序区间为空
 */

#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;

const int maxn=50;
struct node{
    int data;
    node* lchild;
    node* rchild;
};

int pre[maxn],in[maxn],post[maxn];
int n;

node* create(int postL,int postR,int inL,int inR) //后序和中序的区间
{
    if(postL>postR)
        return NULL; 
    node* root=new node;
    root->data=post[postR];  //后序序列中，最后一个节点为根节点
    int k;
    for(k=inL;k<=inR;k++)
    {
        if(in[k]==root->data)
            break;
    }
    int numLeft=k-inL;  //左子区间为左子树0
    root->lchild=create(postL,postL+numLeft-1,inL,k-1);
    root->rchild=create(postL+numLeft,postR-1,k+1,inR);
    return root;
}

int num=0;

void BFS(node *root){
    //层次遍历
    queue<node*> q;
    q.push(root);
    while(!q.empty()){
        node* now=q.front();
        q.pop();
        printf("%d",now->data);
        num++;
        if(num<n)
            printf(" ");
        if(now->lchild!=NULL)
            q.push(now->lchild);
        if(now->rchild!=NULL)
            q.push(now->rchild);
    }
}
int main()
{
    scanf("%d",&n);
    int i;
    for(i=0;i<n;i++){
        scanf("%d",&post[i]);
    }

    for(i=0;i<n;i++){
        scanf("%d",&in[i]);
    }

    node* root=create(0,n-1,0,n-1);
    BFS(root);
    prinf("\n");
    return 0;
}

仅供学习参考！

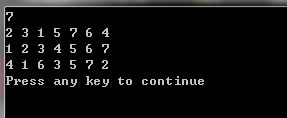
测试用例：【PAT A1020】