[USACO18DEC]Balance Beam
题面
Solution:
现在奶牛要做的决策就是获得随机游走的期望得分还是直接获得该点的得分,显然答案就是在这两者中取max。
我们先来考虑特殊情况:
如果一头奶牛在f的最高点,那么显然随机游走的期望得分是不大于直接跳下去的得分的。
对于一个位置 \(i\) 若 \(u < i < v\) 并且 \(f[u],f[v]\) 都 \(>f[i],\) 那么它肯定想要随机游走到 \(u\) 或 \(v\) 上会更优。
然后我们发现,一个类似于凸包的模型就出来了,于是我们大胆的猜想:
对于平面上的每个点 \((i, f[i])\)
- 对于在凸包上的点,答案就是直接跳下去。
- 对于不在凸包上的点,答案就是随机游走到最近左右两个凸包上的点的期望值。
在证明之前我们先来了解一下序列随机游走问题:
你现在位于坐标轴上的 \(i\) 点 \((l < i < r)\),随机向左或向右走一步,到达 \(l\) 或 \(r\) 时停止,并获得 \(val[l]\) 或 \(val[r]\) 的权值,问期望获得权值为多少。
设 \(i\) 点的期望为 \(f[i]\), 则 \(f[l] = val[l], f[r] = val[r], f[i] = \frac{f[i-1] + f[i + 1]}{2}, l < i < r, i \in N^+\)
我们发现 \(f\) 为一个等差数列,so
\[\begin{aligned}
f[i] &= val[l] + \frac{val[r] - val[l]}{r - l} \times (i - l)\\
&=\frac{(r - i)\times val[l]+(i - l)\times val[r]}{r - l}
\end{aligned}
\]
证明:
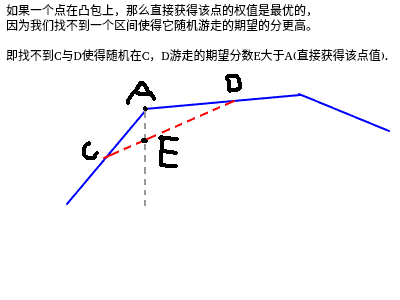
对于不在凸包上的点显然我们也找不到一个比在相邻凸包上的点之间随机游走的更优的解, 画画图就好了。
所以这题就找出上凸包(单调栈维护\(O(n)\)),对于每一个点可以 \(O(1)\) 计算答案。
细节:由于单调栈维护上凸包时要计算斜率,防止精度误差,化一下式子,改成乘法比较。
Source
#include <set>
#include <cmath>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <assert.h>
#include <algorithm>
using namespace std;
#define fir first
#define sec second
#define pb push_back
#define mp make_pair
#define LL long long
#define INF (0x3f3f3f3f)
#define mem(a, b) memset(a, b, sizeof (a))
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define Debug(x) cout << #x << " = " << x << endl
#define travle(i, x) for (register int i = head[x]; i; i = nxt[i])
#define For(i, a, b) for (register int (i) = (a); (i) <= (b); ++ (i))
#define Forr(i, a, b) for (register int (i) = (a); (i) >= (b); -- (i))
#define file(s) freopen(s".in", "r", stdin), freopen(s".out", "w", stdout)
#define ____ debug("go\n")
namespace io {
static char buf[1<<21], *pos = buf, *end = buf;
inline char getc()
{ return pos == end && (end = (pos = buf) + fread(buf, 1, 1<<21, stdin), pos == end) ? EOF : *pos ++; }
inline int rint() {
register int x = 0, f = 1;register char c;
while (!isdigit(c = getc())) if (c == '-') f = -1;
while (x = (x << 1) + (x << 3) + (c ^ 48), isdigit(c = getc()));
return x * f;
}
inline LL rLL() {
register LL x = 0, f = 1; register char c;
while (!isdigit(c = getc())) if (c == '-') f = -1;
while (x = (x << 1ll) + (x << 3ll) + (c ^ 48), isdigit(c = getc()));
return x * f;
}
inline void rstr(char *str) {
while (isspace(*str = getc()));
while (!isspace(*++str = getc()))
if (*str == EOF) break;
*str = '\0';
}
template<typename T>
inline bool chkmin(T &x, T y) { return x > y ? (x = y, 1) : 0; }
template<typename T>
inline bool chkmax(T &x, T y) { return x < y ? (x = y, 1) : 0; }
}
using namespace io;
const int N = 2e5 + 1, M = 1e5;
int n, top, stk[N], l[N], r[N];
LL f[N];
bool chk(int x, int y, int z) {
return (1ll * (f[y] - f[x]) * (z - y)) >= (1ll * (f[z] - f[y]) * (y - x));
}
int main() {
#ifndef ONLINE_JUDGE
file("Balance_Beam");
#endif
ios::sync_with_stdio(0);
n = rint();
For (i, 1, n) f[i] = rint();
stk[++top] = 0;
for (int i = 1; i <= n + 1; ++ i) {
while (top > 1 && !chk(stk[top - 1], stk[top], i)) top --;
stk[++top] = i;
}
for (int i = 1; i < top; ++ i) {
for (int j = stk[i] + 1; j < stk[i + 1]; ++ j)
l[j] = stk[i], r[j] = stk[i + 1];
l[stk[i]] = r[stk[i]] = stk[i];
}
For (i, 1, n) {
if (l[i] == r[i]) printf("%lld\n", 1ll * M * 1ll * f[i]);
else printf("%lld\n", (1ll * M * 1ll * (1ll * f[l[i]] * (r[i] - i) + 1ll * f[r[i]] * (i - l[i]))) / (1ll * (r[i] - l[i])));
}
return 0;
}





