深度学习实战基础
1. 选择合适的目标函数
均方误差: \(\sum\limits_{i=1}^n (y_i-\hat{y}_i)^2=0\),如神经网络里目标函数 \(J(\mathrm{w})={1\over 2}\sum\limits_{k=1}^c (t_k-z_k)^2\)
交叉熵: \(-\sum\limits_{i=1}^n\hat{y}_i\ln y_i=0\) 深度学习里用的比较多。\(\hat{y}_i\) 实际期望值(对于分类问题标签是0或者1),\(y_i\) 计算值。在 \(\ln\) 里,所以计算值不要让它为0,即便很小也要让它为一个很小的数。交叉熵比均方误差有更好的收敛性质,李宏毅实验了交叉熵对于深度学习的模型很快的精度有所提高。可视化二维交叉熵与均方误差的山地图,交叉熵更陡,更容易快速搜索到最优值。
2. softmax 层
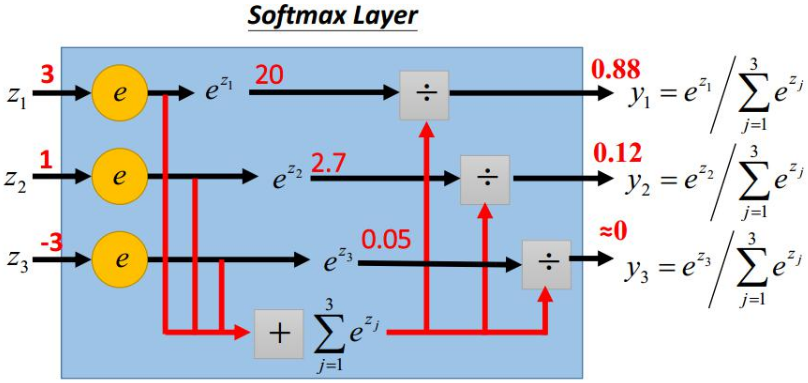
作用是突出最大值,并转换成概率的形式
如何突出? 用 \(\mathbf{e^x}\), 让大的更大,小的更小,而且都大于0(对于交叉熵的 \(\ln\) 需要大于0的处理)。最后归一化,变成概率形式。
看一下\(e^x\):

3. 激活函数
梯度消失的问题
假设神经元的激活函数采用 Sigmoid 的函数,特点是 Sigmoid 的导数函数的最大值是\(1\over 4\), 这样激活函数的导数在多层的连乘,导致梯度值越来越小,相当于0.25的若干次方, 导致梯度消失。另外 \(\mid\mathrm{w}\mid<1\) 用的比较多,可能是经验上初始值设置的小一点权重效果比较好。经验上权重初始分配成正态分布,一般都是小于 1 的。
ReLU
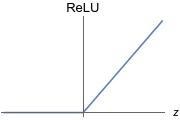
大于0是自己本身,是线性的。能够避免梯度消失的问题

小于0为0,相当于简化了网络,计算快

4. 学习步长
\(\mathrm{w}(m+1)=\mathrm{w}(m)+\Delta \mathrm{w} = \mathrm{w}(m)-\eta\frac{\partial J}{\partial \mathrm{w}}\)
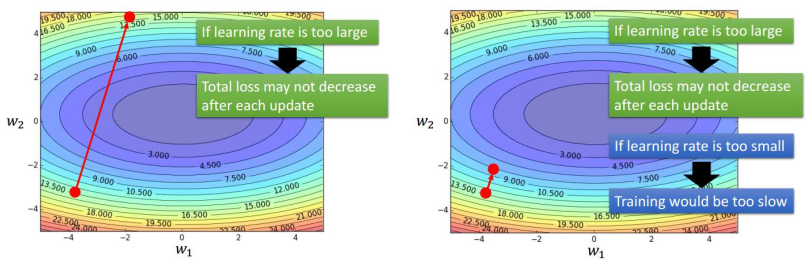
学习步长\(\eta\)过大,目标函数可能不降低;若学习步长过小,训练过程可能非常缓慢。
解决方法:训练几轮后按一些因素调整学习步长。例如:按轮次\(t\), 轮次越多步长越小,这样能够到谷底
随机梯度下降SGD的问题
learning rate 不易确定,如果选择太小,收敛速度会很慢;如果太大,损失函数在极小值处不停地震荡甚至偏离。每个参数的 learning rate 都是相同的。如果数据是稀疏的,应当对出现频率低的特征进行大一点的更新,学习率应当自适应。
深层神经网络另一个问题,陷入马鞍面,在这种区域中,所有方向的梯度值都几乎是0,传统的办法失效。
解决方法: Momentum 动量,借用物理的概念。往前走一点,往前几次的梯度也参与运算,冲出马鞍面,有可能还可以下降
引入新的变量\(v\),\(v\) 是之前的梯度的累加,但每回合都有一定的衰减\(\alpha\), (\(\alpha<1\))
\(g\leftarrow {1\over m}\nabla_w \sum\limits_i^m L(f(x_i;w),y_i)\), \(g\)是梯度值,即\(\frac{\partial J}{\partial \mathrm{w}},\)x_i$ 是样本输入,\(y_i\) 是输出,\(m\) 是样本数, \(\nabla\) 是梯度,\(f\) 是神经网络, L(Lost 或者 Cost) 为损失函数或者代价函数用于比较神经网络计算的输出和实际期望输出\(y_i\)的差距有多大
\(v\leftarrow \alpha v-\eta g\), \(\eta\) 是学习步长;前\(v\)后\(g\)方向一致,加速学习;前后方向不一致,如果不是谷底能够冲过去,如果是谷底,能够带回来,从而抑制震荡
\(w\leftarrow w+v\)
改进:先考虑过往动量,再叠加(Nesterov Momentum)
\(g\leftarrow {1\over m}\nabla_w \sum\limits_i^m L(f(x_i;w\color{green}{+\alpha v}),y_i)\)
\(v\leftarrow \alpha v-\eta g\)
\(w\leftarrow w+v\)

先按动量的方向,相当于 lookahead 往前看了一点,所说效果会好一点。
4.1 Adagrad
为不同的参数设置不同的学习步长
\(g\leftarrow {1\over m}\nabla_w \sum\limits_i^m L(f(x_i;w),y_i)\)
\(r\leftarrow r+g \odot g\), 向量对位乘(相当于梯度做了平方,二阶矩),然后结果累加,式子的值是递增的。
\(\Delta w = -\frac{\eta}{\delta +\sqrt{r}}\odot g\) 梯度越小,缓坡,学习步长越大,相当于可以在缓坡上大步地往下跑;如果陡坡上,梯度大,只能小步地往下挪;相当于调整了学习步长\(\eta\),学习步长自适应;\(\delta\) 为一个很小的数防止分母为\(0\)
\(w\leftarrow w+\Delta w\)
缺点: 调整学习步长的参数\(r\) 是累加一直递增的。如果前面有一个大的梯度,后面就不会再变小了,步长只会越来越小,但是如果有这种需求,希望有个地方步长能够稍微大一点,就不能够解决这种需求。
解决方法:使用衰减系统调整 RMSprop
\(g\leftarrow {1\over m}\nabla_w \sum\limits_i^m L(f(x_i;w),y_i)\)
\(r\leftarrow \color{red}{\rho} r+\color{red}{(1-\rho)}g \odot g\), 使式子的不一定递增,使用\(\rho\) 进行调节,本意不变,本意还是用梯度的平方来调整学习步长。解决Adagrad过早结束的问题,适合处理非平衡目标,对于RNN效果很好
\(\Delta w = -\frac{\eta}{\delta +\sqrt{r}}\odot g\)
\(w\leftarrow w+\Delta w\)
4.2 Adam 自适应矩估计
带动量项的RMSprop方法, 利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率
\(g\leftarrow +{1\over m}\nabla_w \sum\limits_i^m L(f(x_i;w),y_i)\)
\(s\leftarrow \color{red}{\rho_1} s+\color{red}{(1-\rho_1)}g\) 一阶矩
\(r\leftarrow \color{red}{\rho_2} r+\color{red}{(1-\rho_2)}g\odot g\) 二阶矩
\(\hat{s}\leftarrow \frac{s}{1-\rho_1^t}\) 随时间推移,\(\rho_1\) 影响减小,经验值0.9效果比较好
\(\hat{r}\leftarrow \frac{r}{1-\rho_2^t}\) 随时间推移,\(\rho_2\) 影响减小,经验值0.999效果比较好
\(\Delta w = -\eta\frac{\hat{s}}{\delta +\sqrt{\hat{r}}}\odot g\)
\(w\leftarrow w+\Delta w\)
5. 梯度下降方法选择经验
如果数据是稀疏的(稀疏高维,稀疏可能导致权重参数分布的差异性比较大,所以用自适应的方法比较好),就用自适应的方法,如Adagrad, Adadelta, RMSprop, Adam
RMSprop, Adadelta, Adam 在很多情况下效果相似。通常 Adam 是最好的选择。
很多论文里都会用SGD,一般作者手动调参数使其不会被困在鞍点,需要经验。优点是SGD比较稳定。
优先考虑 SGD+Nesterov Momentum 或者 Adam. 其次选择熟悉的算法。再次根据数据,稀疏数据考虑自适应学习率的算法。根据需求,验证模型用Adam,模型上线或者发布结果前,用精调的SGD。先用小数据集进行实验算法的效果来选择,有论文指出随机梯度下降算法的收敛速度和数据集的大小关系不大。算法组合,先用Adam进行快速下降,再用SGD充分调优。 数据集需要 shuffle。要制定学习率的衰减策略,用定期误差策略,或者用精度或AUC性能指标来监控。
6. Batch Normalization
CNN训练绝大多数基于 mini-batch 的随机梯度下降算法。比如一个节点输入西瓜,另一个节点输出芝麻,需要归一化量纲进行预处理,然后再使用随机梯度下降算法。归一化量纲。不同的数据都是均值和离散程度(方差)比较。
- 输入:小批量的一组数据 \(\{x_1,\cdots,x_m\}\);需要学习的参数 \(\gamma\), \(\beta\)
- 输出: \(\{y_i=\mathrm{BN}_{\gamma,\beta}(x_i)\}\)
- \(\mu_{\mathcal{B}}\leftarrow {1\over m}\sum\limits_{i=1}^m x_i\) // 小批量的均值
- \(\sigma_{\mathcal{B}}^2 \leftarrow {1\over m}\sum\limits_{i=1}^m(x_i-\mu_{\mathcal{B}})^2\) // 小批量的方差
- \(\hat{x_i}\leftarrow\frac{x_i-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^2+\epsilon}}\) // 归一化,规范化,均值为0,方差为1
- \(y_i\leftarrow\gamma\hat{x_i}+\beta\equiv\mathrm{BN}_{\gamma,\beta}(x_i)\) // 需要用 \(\gamma\), \(\beta\) 进行调整,使处理后的值能够保留原来的分布信息
7. 避免过适应(过拟合)
只要在测试集中稍微加一些噪声,学习机就不能做出正确的判断
原因是,权重参数太多,样本量不足
解决方法:早期停止训练,权重衰减,Dropout
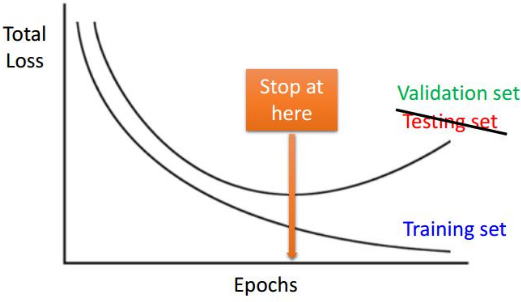
早期停止训练
从训练集里选出一个集合作为验证集。当目标函数在验证集上不再减小时,训练停止。如果继续训练可能是无意义的个性化特征,没有必要,避免过适应应当停止训练。
权重衰减
有些权重是“无用的”, 使用权重衰减方法
原梯度下降公式:\(w\leftarrow w-\eta\frac{\partial J}{\partial w}\)
权重衰减
\(w\leftarrow (1-\lambda)w-\eta\frac{\partial J}{\partial w}\), \(\lambda\) 为误差率,如可为0.01. 其实系统的权重初始化一般取小的值在一定程度也避免过适应。迭代很多次后,如果后面的梯度项很小的话,前面的项也会越来越小趋近于0

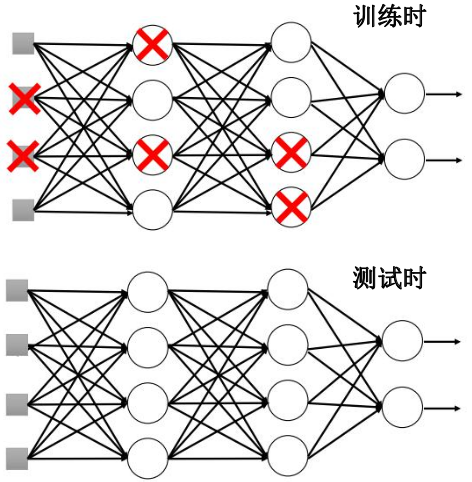
Dropout
每次更新参数前,按对所有神经元一定比例删减部分神经元,每次对所有神经元删减的都不一样;相当于每次使用一个子网络训练。是集成学习的一种。测试阶段,集成所有神经元的结果。删减时相当于权重放大了,所以测试是要缩减所有神经元的权重,比如dropout 50%比例的神经元,测试时,每个神经元的权重相当于训练时的两倍,就应当缩减 50%.
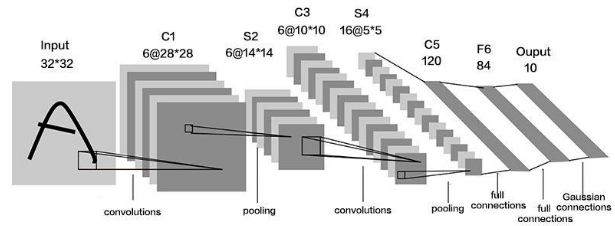
8. 卷积神经网络 CNN
基本组件:卷积层 convolutional layer; 激活函数 (Sigmoid, ReLU等);池化层 Pooling layer, 平均池化average pooling, 最大化池化 Max pooling, 最大化池化 Max pooling; 全连接层 Fully-connected layer
3D滤波器/卷积核
以扫描窗的方式,对图像做卷积;每层含有多个核,每个核对应一个输出通道。提取局部特征;权重参数是学习得到的, 而不像传统机器学习方法,是选择边还是选择轮廓,深度学习学习到的特征是最有助于达到分类目标的。
每一层有多个核(模板),之后的通道数量取决于卷积核的数量。
卷积核的参数:滤波器/卷积核数量,核尺寸 kernel size, 步长, 零填充。一般有套路,比如步长等于2相当于把图片缩小。核尺寸跟零填充的数量也有关系。
非线性激活函数, Sigmoid; ReLU(Rectified Linear Unit) 明显地改善梯度消失问题。
步长
步长大于1,有降维作用。卷完图片缩小。
池化
作用:特征融合,降维,无参数需要学习。
有两种:最大池化,平均池化。专家经验最大池化比平均池化效果好
每四个同样的通道数据里取一个。通道数不变,尺度大小变化。把图片变小(需要的神经元少)的方法:池化和步长等于2 的卷积。
CNN-Softmax 层
指数归一化函数,将一个数值向量压缩到(0,1),变成概率值
所有元素和为1
\(\sigma(\mathrm{z})_j=\frac{e^{z_j}}{\sum_{k=1}^K e^{z_k}},\, for\, j=1,\cdots,k\)
8.1 误差反向传播
用\(a^l\) 表示第\(l\)层的输出, \(a^0\) 表示网络最开始的输入。假设激活函数都是\(\sigma()\), \(a^l=\sigma(z^l)\)
\(w^l\) 和 \(b^l\) 表示第 \(l\) 层的参数, \(z^l\) 是第 \(l\) 层神经元的输入,即\(z^l=w^la^{l-1}+b^l\)
\(\delta^l\)表示第\(l\)层的残差
有\(l\)层的残差:
\(\color{red}{\delta^{l-1}}=\color{orange}{W^{lT}}\color{green}{\delta^l}\odot\color{blue}{\sigma}^\prime(\color{purple}{z^{l-1})}\)
对照BP神经网络:
\(\color{red}{\delta_j}=\color{blue}{f}^\prime(\color{purple}{net_j})\sum\limits_{k=1}^c \color{green}{\delta_k} \color{orange}{w_{kj}}\)
池化层的误差反向传播
已知卷积层的下一层为池化层,已知池化层的残差,求卷积层的残差:
假设第 \(l-1\) 层为卷积层,第 \(l\) 层为池化层,池化层的残差为\(\delta_j^l\), 卷积层的残差为\(\delta_j^{l-1}\),\(\delta_j^{l-1}=UP(\color{green}{\delta_j^l})\odot\color{blue}{\sigma}^\prime(\color{purple}{z_j^{l-1}})\),由于池化层只对图像降维,没有权重和残差相乘,所以池化层操作是对上层残差上采样。上采样时,采用等值复制的方法,然后为了保持总残差不变,上采样的新值要使用平均值 mean-pooling。另外一种保持总残差不变的方法是,记录前向传播中pooling区域中最大值的位置,在相应位置进行恢复,其余位置为0, max pooling
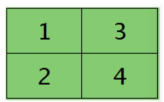

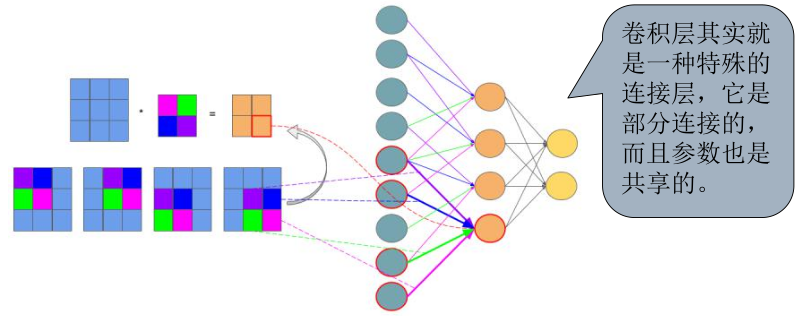
卷积层的运算
展开
\(\begin{pmatrix}\color{red}{a_{11}} & \color{red}{a_{12}} & a_{13}\\ \color{red}{a_{21}} & \color{red}{a_{22}} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{pmatrix}\otimes \begin{pmatrix}\color{red}{w_{11}} & \color{red}{w_{12}}\\\color{red}{w_{21}} & \color{red}{w_{22}}\end{pmatrix}=\begin{pmatrix}\color{red}{z_{11}} & z_{12}\\z_{21} & z_{22}\end{pmatrix}\)
可视化如下图左边,橙色的神经元为 \(z_{11}\)到\(z_{22}\), 青色神经元表示 \(a_{11}\)到\(a_{33}\), 权重,蓝色线表示\(w_{12}\), 紫色线表示\(w_{11}\). 卷积层是部分连接的,不是全连接。
左边没有边填充与\(2\times2\)的卷积核进行卷积
\(\color{red}{z_{11}=a_{11}w_{11}+a_{12}w_{12}+a_{21}w_{21}+a_{22}w_{22}}\)
\(z_{12}=a_{12}w_{11}+a_{13}w_{12}+a_{22}w_{21}+a_{23}w_{22}\)
\(z_{21}=a_{21}w_{11}+a_{22}w_{12}+a_{31}w_{21}+a_{32}w_{22}\)
\(z_{22}=a_{22}w_{11}+a_{23}w_{12}+a_{32}w_{21}+a_{33}w_{22}\)
卷积操作一般是要把卷积核旋转180度再相乘,由于CNN中的卷积参数(卷积核里的权重)是训练过程“学”来的,所以旋转不旋转,关系不大。
卷积层是部分连接的不是全连接的;权重参数共享,比如绿色在几个地方都有。
卷积层的误差反向传播
本层为 \(l\) 层,上一层为\(l-1\) 层。先计算\(\delta^{l-1}\)。\(a^{l-1}\) 是上一层经过一定的操作(激活 active)得到输出,同时也是本层\(l\)层的输入。\(a^{l-1}=\sigma(z^{l-1})\), 无论是卷积层的激活函数还是 pooling 层等 都可以用 \(\sigma()\)来表示。\(z^{l-1}\) 是上一层的输入。
链式法则:
上一层即 \(l-1\) 层的残差是目标函数对 \(l-1\)层输入的偏导。与BP神经网络不一样?(BP神经网络是该层神经元的激活函数对该层输入的偏导再乘以上一层的)
\(\delta^{l-1}=\frac{\partial J}{\partial z^{l-1}}\)
对其链式展开:
由\(a^l=\sigma(z^l)\), \(a^{l-1}=\sigma (z^{l-1})\)
\(\frac{\partial a^{l-1}}{\partial z^{l-1}}=\sigma^\prime(z^{l-1})\)
又由 \(z^l=w^l a^{l-1} +b^l\), \(\frac{\partial z^l}{\partial a^l-1} = w^l\) 不是全连接,存在权重共享,所以不写成全连接矩阵形式\(\color{orange}{W^{lT}}\)
\(\frac{\partial J}{\partial z^{l-1}}=\frac{\partial J}{\partial z^l}\frac{\partial z^l}{\partial a^{l-1}}\frac{\partial a^{l-1}}{\partial z^{l-1}}=\frac{\partial J}{\partial z^l}\color{orange}{\frac{\partial z^l}{\partial a^{l-1}}}\color{green}{\frac{\partial a^{l-1}}{\partial z^{l-1}}}=\delta^l \color{orange}{\frac{\partial z^l}{\partial a^{l-1}}}\odot \color{green}{\sigma^\prime (z^{l-1})}\)
对照BP神经网络:
\(\frac{\partial J}{\partial w_{ji}}=\color{darkorange}{\frac{\partial J}{\partial y_j}}\color{darkgreen}{\frac{\partial y_j}{\partial net_j}}\color{darkgray}{\frac{\partial net_j}{\partial w_{ji}}}=\color{darkorange}{\left[ -\sum\limits_{k=1}^c(t_k-z_k) \frac{\partial z_k}{y_j}\right]}\color{darkgreen}{\frac{\partial y_j}{\partial net_j}}\color{darkgray}{\frac{\partial net_{j}}{\partial w_{ji}}} =\color{darkorange}{\left[ -\sum\limits_{k=1}^c(t_k-z_k) \frac{\partial z_k}{\partial net_k}\frac{\partial net_k}{\partial y_j}\right]}\color{darkgreen}{\frac{\partial y_j}{\partial net_j}}\color{darkgray}{\frac{\partial net_{y_1}}{\partial w_{ji}}} =\color{darkorange}{-(t_k-z_k) \frac{\partial z_k}{\partial net_k}\frac{\partial net_k}{\partial y_j}}\color{darkgreen}{\frac{\partial y_j}{\partial net_j}}\color{darkgray}{\frac{\partial net_j}{\partial w_{ji}}} =\color{darkorange}{-(t_k-z_k) f^\prime(net_k)w_{kj}^*}\color{darkgreen}{g^\prime(net_j)}\color{darkgray}{x_i}=\color{darkgreen}{g^\prime(net_j)}\color{darkorange}{\sum\limits_{k=1}^c \delta_k w_{kj}}\color{darkgray}{x_i}\)
残差=当前层激活函数的导数*上层反传来的误差
\(隐含层 \longrightarrow 输出层\)
\(\delta_k=\color{darkorange}{f^\prime(net_k)}(t_k-z_k)\)
\(输入层 \longrightarrow 隐含层\)
\(\delta_j=\color{darkorange}{\frac{\partial J}{y_j}}\color{darkgreen}{\frac{\partial y_j}{\partial net_j}}=\color{red}{\frac{\partial J}{\partial net_j}}=\frac{\partial 目标函数}{\partial 该层激活后的输出}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{\partial 该层激活后的输出}{\partial 激活前的输入}\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{\partial 目标函数}{\partial 该层激活前的输入}\) 与CNN思路和一样
\(\delta_j=\color{darkgreen}{g^\prime(net_j)}\color{darkorange}{\sum\limits_{k=1}^c \delta_k w_{kj}}\)
\(l-1\) 的残差整理得:
\(\delta^{l-1}=\frac{\partial J}{\partial z^l}\color{orange}{\frac{\partial z^l}{\partial a^{l-1}}}\color{green}{\frac{\partial a^{l-1}}{\partial z^{l-1}}}=\delta^l \color{orange}{\frac{\partial z^l}{\partial a^{l-1}}}\odot \color{green}{\sigma^\prime (z^{l-1})}\)
记目标函数\(J\)对上一层\(l-1\)层的输出\(a^{l-1}\)的偏导 \(\frac{\partial J}{\partial z^l}\color{orange}{\frac{\partial z^l}{\partial a^{l-1}}}=\frac{\partial J}{\partial a_{ij}}=\nabla a_{ij}\)
CNN与全连接层的重要区别就是\(\color{orange}{\frac{\partial z^l}{\partial a^{l-1}}}\),如何计算?展开后,保留权重存在的项
\(\nabla a_{11} = \color{red}{\frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{11}^{l-1}}}+\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{11}^{l-1}}+\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{11}^{l-1}}+\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{11}^{l-1}}=\color{red}{\frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{11}^{l-1}}}=\delta_{11}^l w_{11}^l\)
\(\nabla a_{12} = \color{blue}{\frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{12}^{l-1}}}+\color{blue}{\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{12}^{l-1}}}+\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{12}^{l-1}}+\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{12}^{l-1}}=\color{blue}{\frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{12}^{l-1}}}+\color{blue}{\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{12}^{l-1}}}=\delta_{11}^l w_{12}^l+\delta_{12}^l w_{12}^l\)
\(\nabla a_{13} = \frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{13}^{l-1}}+\color{lightblue}{\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{13}^{l-1}}}+\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{13}^{l-1}}+\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{13}^{l-1}}=\color{lightblue}{\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{13}^{l-1}}}=\delta_{12}^l w_{12}^l\)
\(\nabla a_{21} = \color{lightgreen}{\frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{21}^{l-1}}}+\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{21}^{l-1}}+\color{lightgreen}{\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{21}^{l-1}}}+\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{21}^{l-1}}=\color{lightgreen}{\frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{21}^{l-1}}}+\color{lightgreen}{\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{21}^{l-1}}}=\delta_{11}^l w_{21}^l+\delta_{21}^l w_{11}^l\)
\(\nabla a_{22} = \color{green}{\frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{22}^{l-1}}}+\color{green}{\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{22}^{l-1}}}+\color{green}{\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{22}^{l-1}}}+\color{green}{\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{22}^{l-1}}}=\delta_{11}^l w_{22}^l+\delta_{12}^l w_{21}^l+\delta_{21}^l w_{12}^l+\delta_{22}^l w_{11}^l\)
\(\nabla a_{23} = \frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{23}^{l-1}}+\color{purple}{\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{23}^{l-1}}}+\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{23}^{l-1}}+\color{purple}{\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{23}^{l-1}}}=\color{purple}{\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{23}^{l-1}}}+\color{purple}{\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{23}^{l-1}}}=\delta_{12}^l w_{22}^l+\delta_{22}^l w_{12}^l\)
\(\nabla a_{31} = \frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{31}^{l-1}}+\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{31}^{l-1}}+\color{yellow}{\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{31}^{l-1}}}+\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{31}^{l-1}}=\color{yellow}{\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{31}^{l-1}}}=\delta_{21}^l w_{21}^l\)
\(\nabla a_{32} = \frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{32}^{l-1}}+\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{32}^{l-1}}+\color{darkcyan}{\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{32}^{l-1}}}+\color{darkcyan}{\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{32}^{l-1}}}=\color{darkcyan}{\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{32}^{l-1}}}+\color{darkcyan}{\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{32}^{l-1}}}=\delta_{21}^l w_{22}^l+\delta_{22}^l w_{21}^l\)
\(\nabla a_{33} = \frac{\partial J}{\partial z_{11}^l}\frac{\partial z_{11}^l}{\partial a_{33}^{l-1}}+\frac{\partial J}{\partial z_{12}^l}\frac{\partial z_{12}^l}{\partial a_{33}^{l-1}}+\frac{\partial J}{\partial z_{21}^l}\frac{\partial z_{21}^l}{\partial a_{33}^{l-1}}+\color{pink}{\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{33}^{l-1}}}=\color{pink}{\frac{\partial J}{\partial z_{22}^l}\frac{\partial z_{22}^l}{\partial a_{33}^{l-1}}}=\delta_{22}^l w_{22}^l\)
\(z_{11}=\color{red}{a_{11}w_{11}}+\color{blue}{a_{12}w_{12}}+\color{lightgreen}{a_{21}w_{21}}+\color{green}{a_{22}w_{22}}\)
\(z_{12}=\color{blue}{a_{12}w_{11}}+\color{lightblue}{a_{13}w_{12}}+\color{green}{a_{22}w_{21}}+\color{purple}{a_{23}w_{22}}\)
\(z_{21}=\color{lightgreen}{a_{21}w_{11}}+\color{green}{a_{22}w_{12}}+\color{yellow}{a_{31}w_{21}}+\color{darkcyan}{a_{32}w_{22}}\)
\(z_{22}=\color{green}{a_{22}w_{11}}+\color{purple}{a_{23}w_{12}}+\color{darkcyan}{a_{32}w_{21}}+\color{pink}{a_{33}w_{22}}\)
把\(\nabla_{ij}\) 去掉层数符号 \(l\) 整理成矩阵
\(\begin{pmatrix}\nabla a_{11} & \nabla a_{12} & \nabla a_{13} \\\nabla a_{21} & \nabla a_{22} & \nabla a_{23} \\\nabla a_{31} & \nabla a_{32} & \nabla a_{33} \\\end{pmatrix}=\begin{pmatrix}0 & 0& 0& 0\\0 & \delta_{11}& \delta_{12}& 0\\0 & \delta_{21}& \delta_{22}& 0\\0 & 0& 0& 0\\\end{pmatrix}\otimes \begin{pmatrix}w_{22} & w_{21}\\w_{12} & w_{11}\\\end{pmatrix}\)
\(\delta^{l-1}=\frac{\partial J}{\partial z^{l-1}}=\delta^l \otimes rot180(W^l)\odot \sigma^\prime(z^{l-1})\)
与BP 不同,这里需要将后一层\(l\)的误差\(\delta^l\)改写成矩阵形式,并用0填充到合适的维度,另外这里不是跟\(W^{lT}\)相乘而是跟\(W^l\)旋转180度后,再与其做卷积运算。
示例
假设第 \(l-1\) 层(池化层) 有N个通道,即有N张特征图。第\(l\)层(卷积层)有M个特征,\(l-1\)层中每个通道图都对应有自己的残差。池化层是线性激活函数。
第\(l\)层中第\(j\)个核对\(l-1\)层第\(i\)个通道的残差计算方法:
\(\delta_i^{l-1}=\sum\limits_{j=1}^M\delta_j^l\star w_{ij}\). \(\star\) 表示离散卷积,即卷积核旋转180度后再卷积。另外因为池化层是线性激活函数,所以后面没有相应节点的导数。
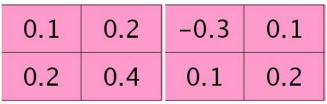
第\(l-1\)层某个通道图,大小为\(3\times3\),第\(l\)层有2个\(2\times 2\)的特征核(权重),则在前向传播卷积时第\(l\)层会有2个大小为\(2\times 2\)的卷积图。
2个特征核(权重):
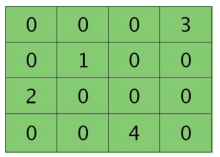
已知第\(l\)层2个卷积图的残差:

求\(l-1\)层的残差:先对\(l\)层残差进行padding然后与特征核进行卷积, \(\star\) 表示将特征核旋转180度后再做卷积
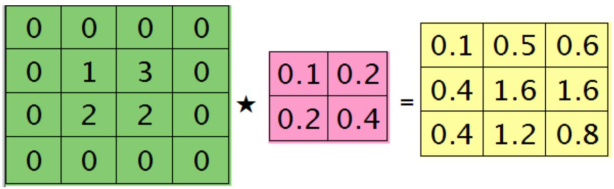

第\(l-1\)层中每个通道图都对应有自己的残差,其结果为第\(l\)层所有特征核的贡献之和,即求第\(i\)通首家的残差时需要将\(l\)层所有核都计算一遍,然后求和。本质上是BP算法。但是这里有重叠,第\(l-1\)层中某个点会对第\(l\)层中的多个点有影响。

有了残差,残差里包含了上一层的误差,然后更新权重的时候需要用到这个残差,相当于接收了上一层的误差,实现了误差的传播。
于是第\(l-1\)层的第\(i\)个通道与第\(l\)层的第\(j\)个通道之间的权值的楄导数(梯度):
\(\frac{\partial J}{\partial w_{ij}}=\delta_j^l \otimes a_i^{l-1}\), \(l\)层\(j\)通道残差与\(l\)层\(j\)通道的输入
\(\frac{\partial J}{\partial b_j} = \delta_j^l\) 关于阈值\(b\)的偏导等于残差
对照BP神经网络:
\(\frac{J}{\partial w_{ji}}=-\delta_j x_i\)
[1] https://blog.csdn.net/cufewxy1/article/details/80445023
[2] https://blog.csdn.net/cufewxy1/article/details/80485886
[3] https://blog.csdn.net/cufewxy1/article/details/80492628
[4] https://cs231n.github.io/convolutional-networks/
[5] https://www.cnblogs.com/pinard/p/6489633.html
[6] https://grzegorzgwardys.wordpress.com/2016/04/22/8/#unique-identifier2
[7] https://www.zhihu.com/question/22298352




 浙公网安备 33010602011771号
浙公网安备 33010602011771号