游戏算法系列 - 字典树
简介
- trie是一种搜索树,也称为字典树。最大的特点是共享字符串的公共前缀来达到提高效率的目的。
- trie的核心思想是空间换时间,缺点是内存占用高
- 最大限度地减少无谓的字符串比较,查询效率比哈希表高
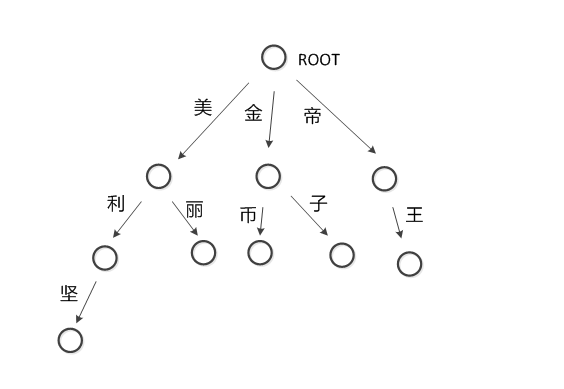
性质
- 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
构建
可以使用链表来实现,每个字符串都是一个链表。
应用
- 词频统计
- 字符串检索
- 字符串搜索的前缀匹配
- ...
游戏屏蔽字替换
问题:假设上图就是游戏屏蔽字,有字符串“你来自美利坚帝国吗?”。需要将敏感词转换为*。
用3个指针来进行操作,分别是p1,p2,p3。p1指向屏蔽字树,p2和p3指向需要检测的字符串
- 把p1指向root节点,p2和p3指向字符串开头的“你”字
- “你”字(p2)不是p1的子节点(当前p1在root节点),把p2和p3移动到下个字符“来”字,p1还是指向root节点
- “来”字(p2)不是p1的子节点(当前p1在root节点),把p2和p3移动到下个字符“自”字,p1还是指向root节点
- “自”字(p2)不是p1的子节点(当前p1在root节点),把p2和p3移动到下个字符“美”字,p1还是指向root节点
- “美”字(p2)是p1的子节点(当前p1在root节点),把p1指向“美”节点,把p2移动到下个字符“利”,p3还是指向字符“美”
- “利”字(p2)是p1的子节点(当前p1指向"美"节点),把p1指向“利”节点,把p2移动到下个字符“坚”,p3还是指向字符“美”
- “坚”字(p2)是p1的子节点(当前p1指向"利"节点),把p1指向“坚”节点,“坚”节点是最后一个节点,查找结束,所以存在敏感词“美利坚”,p3到p2之间的区间就是敏感词,把p3到p2之间的字符都替换成*,最后把p2和p3都移动到字符"帝",p1移动到root节点
- “帝”字(p2)是p1的子节点(当前p1在root节点),把p1指向“帝”节点,把p2移动到下个字符“国”,p3还是指向字符“帝”
- “国”字(p2)不是p1的子节点(当前p1指向"帝"节点),表示以“帝”字开头没有找到敏感词,把p2和p3都移动到字符“国”字,p1指向root节点
- “国”字(p2)不是p1的子节点(当前p1指向root节点),把p2和p3都移动到下个字符“吗”字,p1指向root节点
- “吗”字(p2)不是p1的子节点(当前p1在root节点),把p2和p3移动到下个字符“?”字,p1还是指向root节点
- “?”字(p2)不是p1的子节点(当前p1在root节点),由于"?"已经是最后一个字符了,全部替换结束。
伪代码
func SensitiveTransform(word string) string {
t := []rune(strings.ToLower(word)) // 转换为unicode数组
p1 := tree.GetRoot() // p1指向树的根节点
p2 := t[0] // p2是过滤内容的第一个字符
var p2Index, p3Index int // p2的位置,p3的位置,默认是过滤内容的第一个字符的位置
newWord := word // 过滤后的字符串
// p3指向最后一个字符,则结束
for ; p3Index < len(t); {
// 遍历从p3开始到结尾的字符串
for i := p3Index; i < len(t); i++ {
char := t[i]
if !p1.Contains(p2) {
// 如果p2不是p1子节点,说明以p3开始的内容不需要屏蔽,p3指向下一个位置,p2指向p3,并将p1重置到root节点,终止循环
p2Index = p3Index + 1
p3Index = p3Index + 1
if p2Index < len(t) {
p2 = t[p2Index]
}
p1 = tree.GetRoot()
break
} else {
// 如果p2是p1的子节点,p1节点移动到p2内容对应的节点上,p2移动到下个位置
// 获取p1的子节点
p1 = p1.GetChildNode(char)
// 移动P2到下个位置
p2Index = p2Index + 1
if p2Index < len(t) {
p2 = t[p2Index]
}
if !p1.HasChild() {
// p1没有子节点,树的某条路径遍历完了,说明字符串中含有敏感词
p1 = tree.GetRoot()
// 将敏感词替换成*
temp := []rune(newWord)
newWord = string(temp[:p3Index]) + strings.Repeat("*", p2Index-p3Index) + string(temp[p2Index:])
// p3移动到p2的位置
p3Index = p2Index
}
}
}
}
return newWord
}
时间复杂度
- 匹配字符串:假设字符串的长度为n,我们需要遍历n遍,如果敏感词的长度为m,则最坏的情况下,需要遍历m遍,所以时间复杂度为O(m*n)
- 构建:如果有t个敏感词,每个敏感词的长度是m,那构建trie树的时间复杂度是O(m*t)
实现
基于Golang的实现:https://github.com/MaxwellBackend/Algorithm/tree/master/trie
网络上志同道合,我们一起学习网络安全,一起进步,QQ群:694839022



 浙公网安备 33010602011771号
浙公网安备 33010602011771号