使用动态规划(DP)解决最大公共子串与最大公共子序列问题
首先介绍一下子串和子序列的区别
对于两个字符串 ABCDEF BCYHEF
子序列为字符串中 一定顺序的字符不一定相连
子串为字符串中相连的字符
所以他们的最大公共子序列为 BCEF
最大公共子串为 BC或者EF
那么对于求解最大公共子串和最大公共子序列用什么方法呢,可能我们最开始想到的就是不断的枚举两个的子串或者子序列,再比较哪个最长,这个方法也不是不行,但是对于两个长度分别为n,m的字符串,这个算法的时间复杂为n^m 显然时间复杂度太大,在ACM中这种算法一定会超时的。
那么我们怎么优化呢?
我们发现在枚举的过程中,其实我们其实一直都在重复一个操作,那就是枚举子串,那么我们可以使用动态规划简化这一过程,动态规划正是来处理这种复杂问题简化为多个子问题。
首先来说一下求最大公共子序列的问题
如果你熟悉动态规划算法的话,可以很容易的想出这里的状态转移方程为a[i][j]=max(a[i-1][j],a[i][j-1]) 当然如果你从来都没有接触过动态规划算法也没有关系,这个题还是很基础的。我就先简单的介绍下动态规划算法。
动态规划解决的就是一个最优子结构的问题,什么是最优子结构的呢,就是一个大的问题可以由很多小的子问题组成,当每一个子问题达到最优的时候,我们就可以得到那个大问题的最优解,那么就比如这个问题,求最大公共子序列,那如果我们可以设置一个数组 f[i][j] 表示第一个字符串的前i个元素,与第二个字符串的前j个元素的最大公共子序列,我们让每一个 f[i][j] 都达到了最长,那么最后得到的那个f元素就是我们所要求的答案了。
动态规划问题呢,重点就是求出状态转移方程,状态转移方程就是如何求出 f[i][j] 的方程,
这里的状态转移方程就是
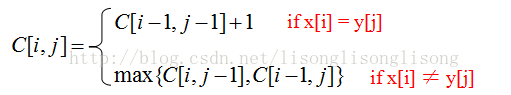
这里用一个矩阵来模拟出我们的选择过程

在最开始做动态规划题目的时候,可能对状态转移方程理解的还不够,使用矩阵来模拟整个过程是一个很好的方法。如图所示,每一个f[i][j]都由他前面数的取值所决定。
这里贴一下我的代码
char str1[100];
char str2[100];
int lcs[100][100];
void Lcs_dp()
{
for (int i=1; i<=n; i++) {
for (int j=1; j<=m; j++) {
if (str1[i]==str2[j]) {
lcs[i][j]=lcs[i-1][j-1];
}
else
{
lcs[i][j]=max(lcs[i-1][j], lcs[i][j-1]);
}
}
}
}
如何求最大公共子串呢
这里同样用矩阵模拟出选择的过程
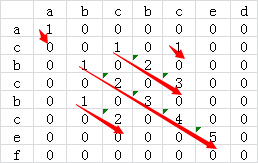
从图中可以看出,整个模拟过程和上面的最大公共子序列很像,唯一的区别就是如果比较到一个地方两个字符串的字符不一样了,我们没有将前面的比较而是直接置零,所以我们将前面的状态转移方程稍微修改即可。
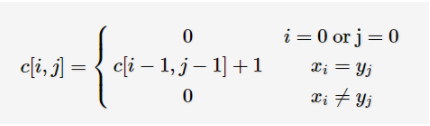
这里我贴一下完整的代码
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
using namespace std;
char str1[100];
char str2[100];
int lcs[100][100]; //最大公共序列的结果
int biggest;
int chuan[100][100]; //最大公共子串
int n,m; //字符串长度
void Lcs_dp()
{
for (int i=1; i<=n; i++) {
for (int j=1; j<=m; j++) {
if (str1[i]==str2[j]) {
lcs[i][j]=lcs[i-1][j-1];
}
else
{
lcs[i][j]=max(lcs[i-1][j], lcs[i][j-1]);
}
}
}
}
void chuan_dp()
{
for (int i=1; i<=n; i++) {
for (int j=1; j<=n; j++) {
if (str1[i]==str2[j]) {
chuan[i][j]=chuan[i-1][j-1]+1;
biggest=biggest>chuan[i][j]?biggest:chuan[i][j];
}
}
}
}
int main()
{
scanf("%s",str1+1);
scanf("%s",str2+1);
n=strlen(str1+1);
m=strlen(str2+1);
Lcs_dp();
chuan_dp();
printf("最大公共子序列:\n");
printf("%d\n",lcs[n][m]);
printf("最大公共子串: \n");
printf("%d\n",biggest);
}*/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号