[LeetCode] 2192. All Ancestors of a Node in a Directed Acyclic Graph

You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).

You are also given a 2D integer array edges, where edges[i] = [fromi, toi] denotes that there is a unidirectional edge from fromi to toi in the graph.

Return a list answer, where answer[i] is the list of ancestors of the ith node, sorted in ascending order.

A node u is an ancestor of another node v if u can reach v via a set of edges.

Example 1:

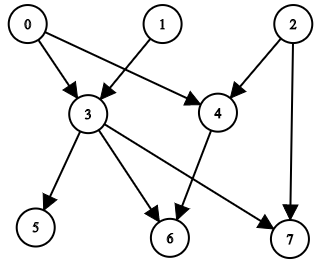
Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.

• Nodes 0, 1, and 2 do not have any ancestors.
• Node 3 has two ancestors 0 and 1.
• Node 4 has two ancestors 0 and 2.
• Node 5 has three ancestors 0, 1, and 3.
• Node 6 has five ancestors 0, 1, 2, 3, and 4.
• Node 7 has four ancestors 0, 1, 2, and 3.

Example 2:

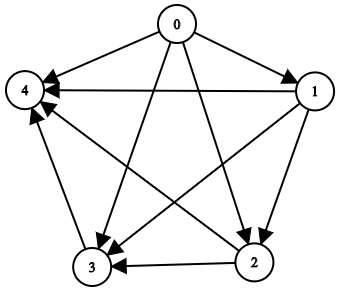
Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Output: [[],[0],[0,1],[0,1,2],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.

• Node 0 does not have any ancestor.
• Node 1 has one ancestor 0.
• Node 2 has two ancestors 0 and 1.
• Node 3 has three ancestors 0, 1, and 2.
• Node 4 has four ancestors 0, 1, 2, and 3.

Constraints:
1 <= n <= 1000
0 <= edges.length <= min(2000, n * (n - 1) / 2)
edges[i].length == 2
0 <= fromi, toi <= n - 1
fromi != toi
There are no duplicate edges.
The graph is directed and acyclic.

有向无环图中一个节点的所有祖先。

给你一个正整数 n ，它表示一个 有向无环图 中节点的数目，节点编号为 0 到 n - 1 （包括两者）。

给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。

请你返回一个数组 answer，其中 answer[i]是第 i 个节点的所有 祖先 ，这些祖先节点 升序 排序。

如果 u 通过一系列边，能够到达 v ，那么我们称节点 u 是节点 v 的 祖先 节点。

思路

这里我用一个类似反向 DFS 的方法解决这道题。题意是找图中每个节点的祖先。因为图本身是有向无环图（DAG），每条边是有方向的，所以为了找祖先，我们可以在建图的时候把每条边反过来理解。比如如果有一条边是从 A 到 B 的，那么我们在建图的时候可以把 A 加到 B 的邻接表上，意思是如果从 B 出发，能走到他的祖先 A。

下面的步骤就跟一般的图的遍历很类似了，我们还是需要一个 boolean 数组记录遍历过程中每个点是否被访问到，具体参见代码。

复杂度

时间O(n)
空间O(n)

代码

Java实现

class Solution {
    public List<List<Integer>> getAncestors(int n, int[][] edges) {
        List<Integer>[] graph = new List[n];
		for (int i = 0; i < n; i++) {
			graph[i] = new ArrayList<>();
		}
		// 反向建图
		for (int[] edge : edges) {
			graph[edge[1]].add(edge[0]);
		}

		List<Integer>[] res = new List[n];
		for (int i = 0; i < n; i++) {
			res[i] = new ArrayList<>();
		}
		boolean[] visited = new boolean[n];
		for (int i = 0; i < n; i++) {
			Arrays.fill(visited, false);
			dfs(graph, visited, i);
			visited[i] = false;		// res[i] 不含 i
			for (int j = 0; j < n; j++) {
				if (visited[j]) {
					res[i].add(j);
				}
			}
		}
		return Arrays.asList(res);
    }

	private void dfs(List<Integer>[] graph, boolean[] visited, int u) {
		visited[u] = true;
		for (int v : graph[u]) {
			if (!visited[v]) {
				dfs(graph, visited, v);
			}
		}
	}
}