[LeetCode] 2368. Reachable Nodes With Restrictions

There is an undirected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an integer array restricted which represents restricted nodes.

Return the maximum number of nodes you can reach from node 0 without visiting a restricted node.

Note that node 0 will not be a restricted node.

Example 1:

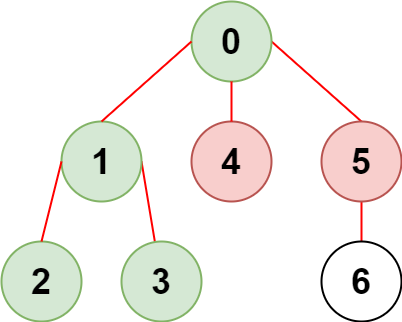
Input: n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
Output: 4
Explanation: The diagram above shows the tree.
We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node.

Example 2:

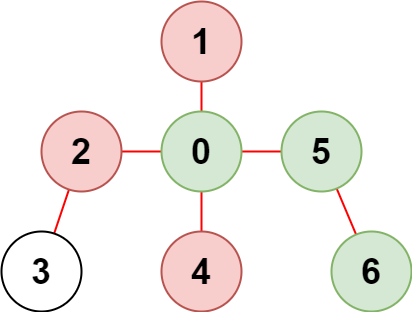
Input: n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
Output: 3
Explanation: The diagram above shows the tree.
We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node.

Constraints:
2 <= n <= 105
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges represents a valid tree.
1 <= restricted.length < n
1 <= restricted[i] < n
All the values of restricted are unique.

受限条件下可到达节点的数目。

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。
给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。
在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目。
注意，节点 0 不 会标记为受限节点。

思路

这道题考的是图的遍历。关于图的题目，基本还是这么几个步骤

• 图的建立
• 图的遍历
• 标记访问过的点避免死循环
• 记录需要的步数或者统计访问过的node个数，这个看具体题目要求

所以这道题的步骤是

• 图的建立
• 图的遍历，这里我用bfs遍历
• 遍历之前先标记那些restricted nodes，这样第一次遇到的时候直接就不访问了
• 用BFS遍历所有能访问到的节点，访问过的节点记得标记成visited
• queue中元素都弹出则说明访问结束，最后返回能访问到的点的个数

复杂度

时间O(n)
空间O(n)

代码

Java实现

class Solution {
    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        List<Integer>[] graph = new List[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }

        for (int[] edge : edges) {
            graph[edge[0]].add(edge[1]);
            graph[edge[1]].add(edge[0]);
        }

        // 处理restricted的node
        boolean[] visited = new boolean[n];
        for (int num : restricted) {
            visited[num] = true;
        }

        // BFS
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(0);
        visited[0] = true;
        int res = 1;
        while (!queue.isEmpty()) {
            int cur = queue.poll();
            for (int next : graph[cur]) {
                if (!visited[next]) {
                    queue.offer(next);
                    visited[next] = true;
                    res++;
                }
            }
        }
        return res;
    }
}