[LeetCode] 2641. Cousins in Binary Tree II
Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins' values.
Two nodes of a binary tree are cousins if they have the same depth with different parents.
Return the root of the modified tree.
Note that the depth of a node is the number of edges in the path from the root node to it.
Example 1:
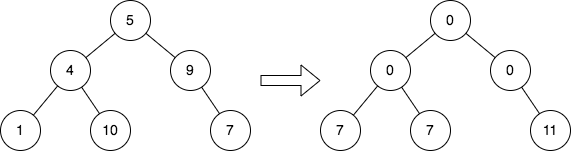
Input: root = [5,4,9,1,10,null,7]
Output: [0,0,0,7,7,null,11]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 5 does not have any cousins so its sum is 0.
- Node with value 4 does not have any cousins so its sum is 0.
- Node with value 9 does not have any cousins so its sum is 0.
- Node with value 1 has a cousin with value 7 so its sum is 7.
- Node with value 10 has a cousin with value 7 so its sum is 7.
- Node with value 7 has cousins with values 1 and 10 so its sum is 11.
Example 2:

Input: root = [3,1,2]
Output: [0,0,0]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 3 does not have any cousins so its sum is 0.
- Node with value 1 does not have any cousins so its sum is 0.
- Node with value 2 does not have any cousins so its sum is 0.
Constraints:
The number of nodes in the tree is in the range [1, 105].
1 <= Node.val <= 104
二叉树的堂兄弟节点 II。
给你一棵二叉树的根 root ,请你将每个节点的值替换成该节点的所有 堂兄弟节点值的和 。
如果两个节点在树中有相同的深度且它们的父节点不同,那么它们互为 堂兄弟 。
请你返回修改值之后,树的根 root 。
注意,一个节点的深度指的是从树根节点到这个节点经过的边数。
思路
这道题跟 993 题版本一类似,节点值的修改规则也涉及到判断两个节点是否互为堂兄弟节点。同时因为堂兄弟节点的其中一个先决条件是两个节点的深度要一样,所以思路会往 BFS 上靠。
这道题的 BFS 做法有些特殊,一般情况下我们只需要用一个 queue 即可做到 BFS。但是这道题我们需要用到两个 list 实现 queue 的功能,一个记录当前层的节点,另一个记录下一层的节点;同时对于树的每一层,我们需要遍历两遍。
当我们遍历当前层的节点的时候,我们需要同时累加下一层的所有节点值的和,记为 nextLevelSum
- 第一遍遍历当前层的时候,我们是为了计算 nextLevelSum
- 第二遍遍历当前层的时候,我们是为了站在当前层去修改下一层的节点值
这个站在当前层去修改下一层的节点值的做法有点类似 117 题。117 题的最优解也是用 BFS 遍历一棵树,站在某一层上去处理下一层的节点的链接。
复杂度
时间O(n)
空间O(n)
代码
Java实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode replaceValueInTree(TreeNode root) {
root.val = 0;
List<TreeNode> q = List.of(root);
while (!q.isEmpty()) {
List<TreeNode> temp = q;
q = new ArrayList<>();
int nextLevelSum = 0;
// 站在当前层统计 nextLevelSum
for (TreeNode node : temp) {
if (node.left != null) {
q.add(node.left);
nextLevelSum += node.left.val;
}
if (node.right != null) {
q.add(node.right);
nextLevelSum += node.right.val;
}
}
// 站在当前层去修改下一层的节点值
for (TreeNode node : temp) {
int childrenSum = (node.left != null ? node.left.val : 0) + (node.right != null ? node.right.val : 0);
if (node.left != null) {
node.left.val = nextLevelSum - childrenSum;
}
if (node.right != null) {
node.right.val = nextLevelSum - childrenSum;
}
}
}
return root;
}
}
相关题目
993. Cousins in Binary Tree
2641. Cousins in Binary Tree II




